1 引言
区域空间结构对于各地经济发展具有重要影响。中国地域辽阔且省份众多,各地城市发展水平不同,其空间结构也有较大差异,从中心城市及其作用来看,有的省份以区域单核结构为主,有的以双核结构为主。区域单核结构一般以省会城市作为区域核心城市;而区域双核结构则存在两个核心城市,一般由省会城市和门户(港口)城市组成。随着区域经济发展,一些省份呈现出明显的区域双核结构特征,如广东省的广州—深圳、福建省的福州—厦门、山东省的济南—青岛、辽宁省的沈阳—大连等。那么,区域双核结构是否会对当地经济发展产生影响?产生何种影响?值得进一步关注及探讨。
区域双核结构的概念最早由陆玉麒提出[1],原指区域中心城市和港口城市及其连线所组成的一种空间结构现象,中心城市与港口城市在空间上的对流与互补决定了双核的共生性。随着区域中心—边缘效应的引入,区域双核结构理论的内涵和应用范围得到进一步拓展,中心城市与沿边城市也被视作次生形态的区域双核结构。一般来说,区域双核结构中的一“核”为区域的政治、经济、文化中心,对整个区域经济发展起辐射带动作用;另一“核”为港口城市或者是沿江、沿河、沿边的门户型城市,起到承接区域对外沟通和资本、要素等的流动作用。陈朋亲等认为基于区域双核结构形成的类似双城联动的合作机制跨越了“行政性障碍”,会优化资源配置,并推动资源、要素自由流动和区域市场一体化为前提的合理化产业分工,进而通过高质量交通等密切了两个中心城市间的联系,并进一步促进当地经济发展[2]。通过梳理相关文献可以发现,目前国内关于区域双核结构的研究尚处于理论探讨阶段而相关实证研究并不多,现有的一些实证研究也大都集中在某一区域或某一省份,缺乏对全国范围内区域双核结构及其影响的相应分析及验证。而现实中呈现出双核结构特征的省份并不少见,那么到底哪些省份属于区域双核结构?其对当地经济有什么影响?均需要进一步探讨。鉴于此,本文采用空间杜宾模型分析中国各省份区域双核结构的分布及其对区域经济发展的影响。
2 文献述评
陆玉麒在研究皖赣地区空间结构时提出了“双核结构”的概念,双核型空间结构被定义为由港口城市与区域中心城市及其连线组成的分布于临海沿江地区的空间结构现象[1]。在后续的研究中,陆玉麒指出通过内涵外延,该模式还可以对沿边地带的区域开发提供重要的指导意义。延伸后的区域双核结构不仅包含中心城市和沿海港口城市组成的空间结构,还包含中心城市与沿江、沿河、沿边等地区的城市所组成的区域空间结构[3]。陆玉麒等针对不同区域的空间特点,分别按照各区域的城市发展和分布情况、自然资源和地理条件等提出了有针对性的建议[4],还提出了区域双核结构的数学推导问题[5],并按形成原因将区域双核结构分为内源型和外生型,其主要区别在于形成区域双核结构的推动力量是内生的还是外生的[6]。之后的研究则开始关注到区域双核结构中的中心城市和港口城市的耦合问题,从区域发展的角度,引用国内外比较典型的区域结构进行了阐述[7]。此外,陆玉麒还探讨了“胡焕庸线”、“T”型模式、区域双核结构的认知过程、产生机理和内在逻辑,进一步探讨了中国空间格局的分布规律[8]。
其他学者对区域双核结构也做了进一步探讨。桑义明等分析了广州的区域双核结构演化历程,探讨了港口城市和中心城市各自的功能以及二者之间的互动关系[9]。盛科荣等以山东省的济南和青岛组成的区域双核结构为例,研究了规模经济和对外贸易对于区域双核结构的影响[10]。王海飞以兰州和西宁为例,从产业结构的角度分析了中心城市和港口城市之间产业的关系[11]。甘霖等以空间相互作用引力模型作为区位潜力的测度并运用山东省进行了实证检验[12]。马颖忆等构建综合指标衡量区域双核结构城市的中心性和门户性,分析了云南省各县以及地级市的中心性和门户性指标[13]。刘秉镰等认为双核结构理论是基于增长极理论和发展轴理论提出的“创新性”双核类型理论,并将其归纳为国内区域经济理论发展中的重要理论之一[14]。
笔者认为,一方面,区域双核结构事实上兼顾了双核心城市的中心性以及门户性,其中,中心城市对周边地区起到更大的辐射作用,门户城市对贸易交流起到更大的促进作用;而作为核心城市,不能在其中某一项指标上过于弱小,均需同时具备一定的中心性及门户性,否则就无法起到中心城市带动区域经济发展和对外贸易的作用。另一方面,中国幅员辽阔但多数省会城市规模尚不够大,中心城市的经济辐射半径不够长,对周边地区的辐射带动作用也有限,而区域双核结构则在一定程度上弥补了这一缺陷;与单核结构相比,核心城市数量更多的双核结构对区域发展具有相对更广泛的辐射范围和带动作用。另外,双核结构更符合中国幅员辽阔、部分地区核心城市发展不足的实际情况,并体现出区域经济特色及理论针对性。
通过文献回顾可以发现,区域双核结构的概念自提出后不断完善,并逐步从理论探讨走向实证分析和验证。但总的来看,目前相关实证分析主要是关于个别省份的分析,而从全国层面进行的实证分析还较为鲜见,尤其是随着城镇化进程的加快,当前哪些省份属于双核结构?其对省域经济发展、产业集聚、科技创新等具有什么影响?需要进一步探讨,这也是本文的分析目的及创新所在。
3 指标说明及计算
3.1 中心性和门户性指标
区域双核结构兼顾了双核心城市的中心性和门户性,具有对内支撑区域内经济发展,对外促进区域贸易、要素交流等作用,因此双核心城市的确定需要考虑城市的中心性和门户性两方面指标综合考量。其中,中心性指的是城市为周边城市提供服务,带动周边城市发展的性质;门户性主要是指城市承担的对外商贸交流等的性质。为了更准确地筛选出区域双核城市并做进一步分析,在实证分析中注重兼顾中心性和门户性两个指标,基于聚类分析结果分别为两个指标划定一个最低门槛值,只有两个指标均达到或超过最低值的城市,才能进入区域双核城市的范围。这是因为中心性和门户性均较低的城市,对于区域经济发展影响较小,因此不宜入选本文所分析的核心城市;而假如某个城市只是某一指标较高,但另一指标偏低,其影响非常有限很难起到核心城市带动省域发展的预期作用,也不适合入选双核城市。
表1 中心性和门户性指标体系
Tab. 1
| 系统层 | 子系统层 | 指标层 |
|---|---|---|
| 中心性 | 中心规模(0.2) | 地区生产总值(亿元)(0.5)、年末总人口(万人)(0.5) |
| 中心经济发展水平(0.3) | 二产产值(亿元)(0.3)、三产产值(亿元)(0.32)、固定资产投资(亿元)(0.22)、职工平均工资(万元/人)(0.16) | |
| 中心社会发展水平(0.2) | 地方一般公共预算支出(亿元)(0.52)、社会消费品零售总额(亿元)(0.48) | |
| 中心交通通达水平(0.15) | 区内可达性(h)(1) | |
| 中心行政等级(0.15) | 省、市政府驻地(1) | |
| 门户性 | 门户规模(0.2) | 地区生产总值(亿元)(0.5)、城市常住人口(万人)(0.5) |
| 门户设施水平(0.3) | 口岸等级(0.4)、货运总量(万t)(0.17)、机场等级(0.28)、火车站等级(0.15) | |
| 门户便捷性(0.25) | 区域可达性(1) | |
| 门户对外依存度(0.25) | 进出口总额/GDP总额(%)(0.6)、实际利用外资/固定资产投资(%)(0.4) |
中心性指标包括中心规模、中心经济发展水平、中心社会发展水平、中心交通通达水平和中心行政等级5个子系统层,并以10项具体指标进行测度;门户性指标包括门户规模、门户设施水平、门户便捷性和门户对外依存度4个子系统层,并以9项具体指标进行测度。对地区生产总值等数据采取对数化处理,进出口总额以当年利率换算为人民币数值,各子系统层和具体指标的系数由熵值法判定[15]。
对没有原始数据的4个指标,参考王毅等[15]的做法,采用专家打分法赋值如下:口岸等级:一、二类口岸分别赋值1、0.5,无口岸赋值0;机场等级4F、4E、4D、4C、3C级分别赋值1、0.8、0.6、0.4、0.2;火车站等级特等、一等、二等、三等、四等、五等站分别赋值1、0.8、0.6、0.4、0.2、0.1。此外,由于测度中心性和门户性的各指标如GDP、进出口总额/GDP总额等数值之间差异较大,本文采用极值标准化法对数据进行处理,极差标准化法公式为:
式中:X为各项具体指标;
3.2 中心性和门户性指标测算及得分
实证分析采用中心性和门户性指标测算部分变量,这也可能会产生内生性问题,因此拟先测算部分不同年份各省份的地级市的中心性和门户性指标,进而确定各省份的空间结构在不同年份是否稳定;如果稳定,则可以认为在回归分析中不会产生内生性问题。
从区域发展现实来看,自双核结构提出以来,地区双核心城市的建设问题逐渐引起关注,尤其是2001年省域副中心城市概念的提出,更进一步促进了省级双核心城市的建设及发展。随着各省逐渐加大省域副中心城市的建设力度,各省区域双核结构的分布情况也产生了明显变化。为体现这些阶段性变化,本文以2001年为节点,以5年为间隔,分别测算回归分析之前的2001年、2006年和回归分析中包含的2009年、2014年以及2019年,各省份地级市中心性和门户性指标,筛选、确定具有双核结构特征的省份并在此基础上进行实证回归分析。
本文测算的259个地级市(2006年、2009年、2014年和2019年全国共279个地级市,但2001年内蒙古、广西、甘肃和宁夏有部分地级市涉及到撤区设市,因此所选样本量共259个地级市,数据暂未包含港澳台地区)相关数据来源于《中国统计年鉴》及各省份统计年鉴,地理距离的数据根据各地级市经纬度的数据测算得出,对于缺失的部分数据采取插值法进行补充。需要说明的是,2001年各地级市进出口数据和2019年地级市货运总量数据存在大量缺失,故把2001年门户性指标中的进出口指标删除,把实际利用外资/固定资产投资的权重赋值为0.25,2019年采用地级市公路货运量代替货运总量数据。考虑到数据的可得性,删除了青海、西藏和海南省,同时考虑到历史因素及邻近性等因素对重庆市和四川省合并处理。经过计算并筛选出中国各省份地级市中心性和门户性的指标得分排名前两名的城市,结果如表2所示。
表2 中国各省份地级市中心性和门户性指标数据
Tab. 2
| 省份 | 城市 | 2001年 | 2006年 | 2009年 | 2014年 | 2019年 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 中心性 | 门户性 | 中心性 | 门户性 | 中心性 | 门户性 | 中心性 | 门户性 | 中心性 | 门户性 | ||||||
| 广东 | 广州 | 0.9469 | 0.6198 | 0.7875 | 0.6884 | 0.7820 | 0.6553 | 0.7627 | 0.6774 | 0.6917 | 0.7361 | ||||
| 深圳 | 0.7587 | 0.5320 | 0.7301 | 0.7453 | 0.7065 | 0.6612 | 0.7000 | 0.7541 | 0.7480 | 0.7782 | |||||
| 四川 | 成都 | 0.6341 | 0.5213 | 0.5470 | 0.5360 | 0.5827 | 0.5330 | 0.5834 | 0.5674 | 0.6142 | 0.6541 | ||||
| 重庆 | 0.6860 | 0.6161 | 0.6744 | 0.6153 | 0.7365 | 0.6473 | 0.7746 | 0.6919 | 0.8040 | 0.7542 | |||||
| 江苏 | 南京 | 0.5155 | 0.5412 | 0.4967 | 0.5900 | 0.5072 | 0.5662 | 0.4855 | 0.5775 | 0.4948 | 0.5970 | ||||
| 苏州 | 0.5581 | 0.3567 | 0.6127 | 0.5074 | 0.6286 | 0.4334 | 0.5825 | 0.4498 | 0.5636 | 0.4755 | |||||
| 浙江 | 杭州 | 0.5473 | 0.5308 | 0.5117 | 0.6011 | 0.5174 | 0.5817 | 0.4819 | 0.5844 | 0.4964 | 0.6177 | ||||
| 宁波 | 0.5048 | 0.4462 | 0.4726 | 0.5248 | 0.4705 | 0.4843 | 0.4313 | 0.5229 | 0.4322 | 0.5212 | |||||
| 山东 | 济南 | 0.5063 | 0.5157 | 0.4427 | 0.5217 | 0.4567 | 0.5161 | 0.4187 | 0.5089 | 0.4395 | 0.5434 | ||||
| 青岛 | 0.4772 | 0.5271 | 0.4822 | 0.5972 | 0.4883 | 0.4970 | 0.4681 | 0.5299 | 0.4465 | 0.5404 | |||||
| 湖北 | 武汉 | 0.5553 | 0.5748 | 0.4899 | 0.6069 | 0.5280 | 0.6000 | 0.5468 | 0.6117 | 0.5507 | 0.6884 | ||||
| 襄阳 | 0.3005 | 0.3289 | 0.2551 | 0.3315 | 0.2735 | 0.3330 | 0.2985 | 0.3404 | 0.2967 | 0.3550 | |||||
| 辽宁 | 沈阳 | 0.5087 | 0.4465 | 0.4800 | 0.4690 | 0.5077 | 0.4644 | 0.4533 | 0.4270 | 0.3555 | 0.4873 | ||||
| 大连 | 0.4957 | 0.4696 | 0.4534 | 0.5057 | 0.4842 | 0.4946 | 0.4465 | 0.5202 | 0.3493 | 0.4741 | |||||
| 湖南 | 长沙 | 0.4307 | 0.4986 | 0.4112 | 0.5338 | 0.4629 | 0.5394 | 0.4696 | 0.5865 | 0.4608 | 0.5905 | ||||
| 岳阳 | 0.3296 | 0.4005 | 0.2762 | 0.4030 | 0.2940 | 0.4170 | 0.2929 | 0.4095 | 0.2911 | 0.4472 | |||||
| 黑龙江 | 哈尔滨 | 0.4231 | 0.3706 | 0.3811 | 0.3700 | 0.3947 | 0.3621 | 0.3650 | 0.3696 | 0.3231 | 0.3388 | ||||
| 大庆 | 0.3650 | 0.1555 | 0.2851 | 0.1445 | 0.3038 | 0.1773 | 0.2709 | 0.1986 | 0.2163 | 0.1746 | |||||
| 河北 | 石家庄 | 0.4306 | 0.5018 | 0.3849 | 0.5023 | 0.3987 | 0.4903 | 0.3763 | 0.5008 | 0.3427 | 0.5279 | ||||
| 唐山 | 0.3676 | 0.3827 | 0.3682 | 0.3901 | 0.4028 | 0.3857 | 0.3628 | 0.4247 | 0.3231 | 0.4242 | |||||
| 河南 | 郑州 | 0.4974 | 0.5287 | 0.4549 | 0.5488 | 0.4793 | 0.5589 | 0.4942 | 0.5971 | 0.5085 | 0.6236 | ||||
| 洛阳 | 0.3431 | 0.4365 | 0.3316 | 0.4514 | 0.3448 | 0.4629 | 0.3221 | 0.4655 | 0.3262 | 0.4866 | |||||
| 陕西 | 西安 | 0.4262 | 0.4762 | 0.3821 | 0.5036 | 0.4249 | 0.5053 | 0.4187 | 0.5292 | 0.4294 | 0.5878 | ||||
| 咸阳 | 0.2886 | 0.3004 | 0.2513 | 0.3017 | 0.2721 | 0.3011 | 0.2725 | 0.3065 | 0.2550 | 0.3049 | |||||
| 吉林 | 长春 | 0.3879 | 0.3966 | 0.3524 | 0.4164 | 0.3784 | 0.3743 | 0.3542 | 0.4198 | 0.3159 | 0.3684 | ||||
| 吉林 | 0.2839 | 0.1277 | 0.2607 | 0.1307 | 0.2901 | 0.1288 | 0.2575 | 0.1323 | 0.2155 | 0.1283 | |||||
| 福建 | 福州 | 0.4297 | 0.4683 | 0.3560 | 0.4800 | 0.3763 | 0.4506 | 0.3777 | 0.4668 | 0.3883 | 0.4566 | ||||
| 厦门 | 0.3767 | 0.4190 | 0.3204 | 0.5229 | 0.3309 | 0.4878 | 0.3066 | 0.5673 | 0.3192 | 0.5072 | |||||
| 云南 | 昆明 | 0.3499 | 0.3184 | 0.3039 | 0.3286 | 0.3226 | 0.3231 | 0.3082 | 0.4394 | 0.3133 | 0.4216 | ||||
| 曲靖 | 0.2595 | 0.1713 | 0.2378 | 0.1818 | 0.2549 | 0.1755 | 0.2372 | 0.1715 | 0.2437 | 0.1825 | |||||
| 安徽 | 合肥 | 0.3854 | 0.3996 | 0.3532 | 0.4374 | 0.4016 | 0.4216 | 0.4122 | 0.5296 | 0.4374 | 0.5577 | ||||
| 芜湖 | 0.3660 | 0.3861 | 0.2976 | 0.4310 | 0.3270 | 0.4164 | 0.3311 | 0.4431 | 0.3315 | 0.4528 | |||||
| 江西 | 南昌 | 0.3294 | 0.4700 | 0.3126 | 0.5132 | 0.3325 | 0.4988 | 0.3379 | 0.5076 | 0.3282 | 0.5208 | ||||
| 九江 | 0.2827 | 0.4224 | 0.2508 | 0.4561 | 0.2642 | 0.4480 | 0.2717 | 0.4628 | 0.2739 | 0.4841 | |||||
| 山西 | 太原 | 0.3446 | 0.4566 | 0.3173 | 0.5062 | 0.3306 | 0.4565 | 0.3005 | 0.4770 | 0.2961 | 0.4465 | ||||
| 长治 | 0.3034 | 0.2838 | 0.2654 | 0.2904 | 0.2821 | 0.2870 | 0.2631 | 0.2883 | 0.2519 | 0.3135 | |||||
| 广西 | 南宁 | 0.3916 | 0.3970 | 0.3148 | 0.4263 | 0.3430 | 0.4303 | 0.3353 | 0.4370 | 0.3282 | 0.4466 | ||||
| 桂林 | 0.3061 | 0.4233 | 0.2611 | 0.4241 | 0.2794 | 0.4258 | 0.2674 | 0.4224 | 0.2559 | 0.4186 | |||||
| 内蒙古 | 呼和浩特 | 0.2373 | 0.3743 | 0.2551 | 0.4114 | 0.2812 | 0.4166 | 0.2500 | 0.4021 | 0.2217 | 0.3884 | ||||
| 包头 | 0.2318 | 0.3439 | 0.2654 | 0.3817 | 0.3107 | 0.3729 | 0.2736 | 0.3636 | 0.2293 | 0.3470 | |||||
| 贵州 | 贵阳 | 0.2654 | 0.4018 | 0.2417 | 0.4076 | 0.2556 | 0.4042 | 0.2562 | 0.4338 | 0.2624 | 0.4642 | ||||
| 遵义 | 0.2486 | 0.2067 | 0.2302 | 0.2043 | 0.2501 | 0.2073 | 0.2460 | 0.2194 | 0.2568 | 0.2976 | |||||
| 甘肃 | 兰州 | 0.2982 | 0.3653 | 0.2519 | 0.3716 | 0.2638 | 0.3625 | 0.2524 | 0.3752 | 0.2478 | 0.3671 | ||||
| 天水 | 0.2406 | 0.2027 | 0.2093 | 0.1981 | 0.2210 | 0.2156 | 0.2097 | 0.2166 | 0.2074 | 0.2162 | |||||
| 新疆 | 乌鲁木齐 | 0.2357 | 0.2595 | 0.2142 | 0.2776 | 0.2444 | 0.2703 | 0.2323 | 0.2766 | 0.2227 | 0.2703 | ||||
| 克拉玛依 | 0.2088 | 0.0071 | 0.1883 | 0.0594 | 0.2002 | 0.0839 | 0.1726 | 0.0862 | 0.1677 | 0.0827 | |||||
| 宁夏 | 银川 | 0.2527 | 0.2208 | 0.2271 | 0.2368 | 0.2538 | 0.2583 | 0.2371 | 0.2771 | 0.2319 | 0.2677 | ||||
| 吴忠 | 0.2416 | 0.1558 | 0.1984 | 0.1558 | 0.2167 | 0.1516 | 0.1992 | 0.1523 | 0.1972 | 0.1519 | |||||
中心性指标方面,2001年中国各省份地级市该指标平均值为0.3991分,最大值为广东省广州市,得分0.9469;最小值为新疆维吾尔自治区克拉玛依市,得分0.2088。2006年的平均值为0.3635分,最大值为广州市,得分0.7875;最小值仍为克拉玛依市,得分0.1883。2009年的平均值为0.3846分,最大值为广州市,得分0.7820;最小值为克拉玛依市,得分0.2002。2014年的平均值为0.3701分,最大值为重庆市,得分0.7746;最小值为克拉玛依市,得分0.1726。2019年的平均值为0.3604分,最大值为重庆市,得分0.8040;最小值仍为克拉玛依市,得分0.1677。总体来看,不同年份的中心性指标得分略有变动但幅度不大。
门户性指标方面,2001年中国各省份的地级市该指标平均值为0.3908分,最大值为广东省广州市,得分为0.6198;最小值是新疆维吾尔自治区克拉玛依市,得分为0.0071。2006的平均值为0.4216分,最大值为广东省深圳市,得分为0.7453;最小值是克拉玛依市,得分为0.0594。2009年的平均值为0.4112分,最大值为深圳市,得分0.6612;最小值为克拉玛依市,得分0.0839。2014年的平均值为0.4317分,最大值为深圳市,得分0.7541;最小值为克拉玛依市,得分0.0862。2019年的平均值为0.4435分,最大值为深圳市,得分0.7782;最小值仍为克拉玛依市,得分0.0827。可以看出,各地级市的门户性指标得分在不同年度变化幅度也不大。
从各年份地级市中心性和门户性指标得分来看,初步分析即能判断出具有典型“中心—门户”特征区域双核结构的省份有:广东省广州—深圳,山东省济南—青岛,辽宁省沈阳—大连,福建省福州—厦门,其他省份则各具不同特性。
分南北方地区来看,南方大部分省份地级市的中心性和门户性指标得分都很高,省会城市与另一城市在中心性和门户性指标得分的差距也较小;而北方大部分省份的省会城市和排名第2城市的门户性指标得分差距较大,排名第2城市的中心性指标得分也较低。这初步说明目前各省份的核心城市建设还存在明显的区域差异。相对来说,南方及东部地区大部分省份的核心城市发展较好,对于本地经济发展的正向影响更为显著;但对于北方及中西部地区的部分省份来说,核心城市还没有得到较好的发展,省会城市往往在省域内“一家独大”但规模不强,次核心城市的建设也有待进一步加强。
3.3 区域双核结构特征省份的筛选及确定
为确定具有区域双核结构特征的省份,本文采取平均数聚类分析法依据各地级市在各时间节点的指标得分进行筛选。同时,为确保结果稳健,分别选取了欧式距离、欧式平方距离、绝对值距离、最大值距离作为相异性指标,进行4次聚类分析,选择在4次聚类分析中均满足相关条件的城市作为核心城市。
综合中心性和门户性指标得分聚类分析结果来看,可以把各地级市按两项指标得分情况分为4类,即高中心性—高门户性城市、高中心性—低门户性城市、低中心性—高门户性城市、低中心性—低门户性城市。本文选取高中心性—高门户性城市作为核心城市选择标准,进而把两个城市均符合这一特征的省份确定为区域双核结构。经过筛选后,仍有一些省份的地级市中心性和门户性本身较低,如果按照聚类分析方法判别双核城市的标准,那么该省份将没有达到中心性和门户性标准的核心城市;因此本文将结合各省份的实际情况与中心性门户性指标得分的差值,进一步判断这些省份的空间结构。
根据聚类分析的结果,从各省份的地级市中心性和门户性指标得分可以确定,区域双核结构的省份有广东省、江苏省、浙江省、山东省、辽宁省、河北省、河南省、福建省、安徽省及四川省(与重庆合并分析);单核结构的省份有湖北省、湖南省、黑龙江省、陕西省、山西省、吉林省、江西省及广西壮族自治区。其他省份则需要进一步单独甄选分析。
需要说明的是,本文在确定区域双核结构的过程中综合参照中心性和门户性两个指标的得分进行分类,部分省份的一些地级市可能存在某一项得分较低的情况,故未能列入本文分析的“核心城市”范围,如黑龙江省齐齐哈尔市、山西省大同市,其门户性指标得分均较低。此外,江苏省等有多个地级市的中心性和门户性指标得分满足核心城市的指标标准,在一定程度上呈现出多中心空间结构的特征,但由于本文的研究主旨是探讨区域双核结构的影响,并未从多中心结构角度进行探讨,因此只保留了这些省份前两名的地级市并将其列为区域双核结构。另外,湖南省岳阳市仅有一年(2001年)满足聚类条件,但其他年份均不满足,综合来看,仍旧把湖南省归类为单核结构省份。
其他省份中,因为其地级市的中心性和门户性指标得分均较低,无法直接确定其空间结构特征,因此按照实际情况和地级市中心性和门户性差值大小来确定是否为区域双核结构。其中,内蒙古自治区呼和浩特市和包头市的中心性指标得分接近,同时门户性指标得分差距也较小,而其他多数省份的地级市之间中心性或者门户性指标得分差距较大。因此,最后确定内蒙古自治区为区域双核结构,贵州省、云南省、甘肃省、新疆维吾尔自治区和宁夏回族自治区为区域单核结构。综上所述,本文最后确定的具有双核结构的省份有11个,单核结构的省份有13个(表3)。
表3 中国各省份空间结构情况
Tab. 3
| 类型 | 省份 |
|---|---|
| 单核结构 | 湖北 湖南 黑龙江 吉林 云南 江西 陕西 山西 贵州 甘肃 新疆 宁夏 广西 |
| 双核结构 | 广东 四川 江苏 浙江 山东 辽宁 河南 河北 福建 内蒙古 安徽 |
4 模型设计和实证分析
4.1 模型设计
地理学第一定理指出,任何事物都是与其他事物相联系的,但是较近的事物比较远的事物的影响更大。而在计量分析中,空间面板数据计量模型旨在研究具有空间相关性变量的回归计量问题,一般可以分为空间自回归模型SAR,空间误差模型SEM以及空间杜宾模型SDM。本文旨在研究中国各省份的区域双核结构对区域经济发展的影响,考虑到现实中各省份的经济发展会受到周边区域的影响,因此本文采用空间杜宾模型进行回归分析。一般空间面板数据的模型为:
式中:
本文选取2009—2019年中国各省份的面板数据进行空间面板数据回归分析。需要说明的是,考虑到疫情的影响,并没有把2020年加入到回归分析中。因此本文选取2009—2019作为研究样本的起止时间。相关变量的描述性统计如表4所示。
表4 各变量描述性统计
Tab. 4
| 变量 | 观测量 | 平均值 | 标准差 | 最小值 | 最大值 |
|---|---|---|---|---|---|
| pgdp | 264 | 10.626 | 0.439 | 9.303 | 11.725 |
| inv | 264 | 0.836 | 0.232 | 0.279 | 1.447 |
| con | 264 | 0.37 | 0.057 | 0.239 | 0.511 |
| afc | 264 | 0.02 | 0.015 | 0 | 0.099 |
| gov | 264 | 0.237 | 0.086 | 0.096 | 0.457 |
| col | 264 | 0.018 | 0.004 | 0.008 | 0.029 |
空间杜宾模型解释变量的效应可以分解为直接效应、间接效应以及总效应。直接效应是本区域的解释变量对于本区域被解释变量的直接影响,而间接效应是其他区域相应解释变量的变化对于本区域被解释变量的影响。直接效应和间接效应均可以分解为两种作用途径,一种是直接影响本区域的被解释变量,另一种是通过空间溢出效应影响其他区域被解释变量进而影响本区域的被解释变量。
本文在计量分析中,将利用各省份的地理相邻矩阵W,首先计算被解释变量的莫兰指数,检验是否存在空间相关关系。如果存在空间相关关系则需要进行空间面板数据的最大似然估计,并检验空间杜宾模型是否会退化为空间自回归模型或空间误差模型;如果不存在空间相关关系则进行普通最小二乘回归分析。
Moran's I指数的计算公式如下所示:
式中:I为全局莫兰指数,用于衡量区域相关经济变量是否存在总体空间相关性;Ii为局部莫兰指数,用于衡量不同时间不同区域之间相关变量是否存在空间相关性;wij为空间权重矩阵W的第i行第j列的数值,当区域i、j地理上是相邻的省份时,wij取值为1,否则wij取值为0;xi和xj为区域i和j的相关经济变量。莫兰指数的绝对值越大表明区域之间的空间相关性越强。
4.2 实证分析
为了利用空间面板数据的相关模型进行回归,检验区域双核结构对于各省份经济发展的影响效果,本文首先计算2009—2019年中国各省份人均地区生产总值的Moran's I和Geary's C及其双侧检验概率,结果如表5所示。
表5 中国各省份人均GDP全局Moran's I和Geary's C指数
Tab. 5
| Moran's I | 变量 | I | E(I) | sd(I) | z | P值 |
|---|---|---|---|---|---|---|
| pgdp | 0.558 | -0.004 | 0.043 | 12.937 | < 0.001 | |
| Geary's C | 变量 | c | E(c) | sd(c) | z | P值 |
| pgdp | 0.453 | 1.000 | 0.047 | -11.515 | < 0.001 |
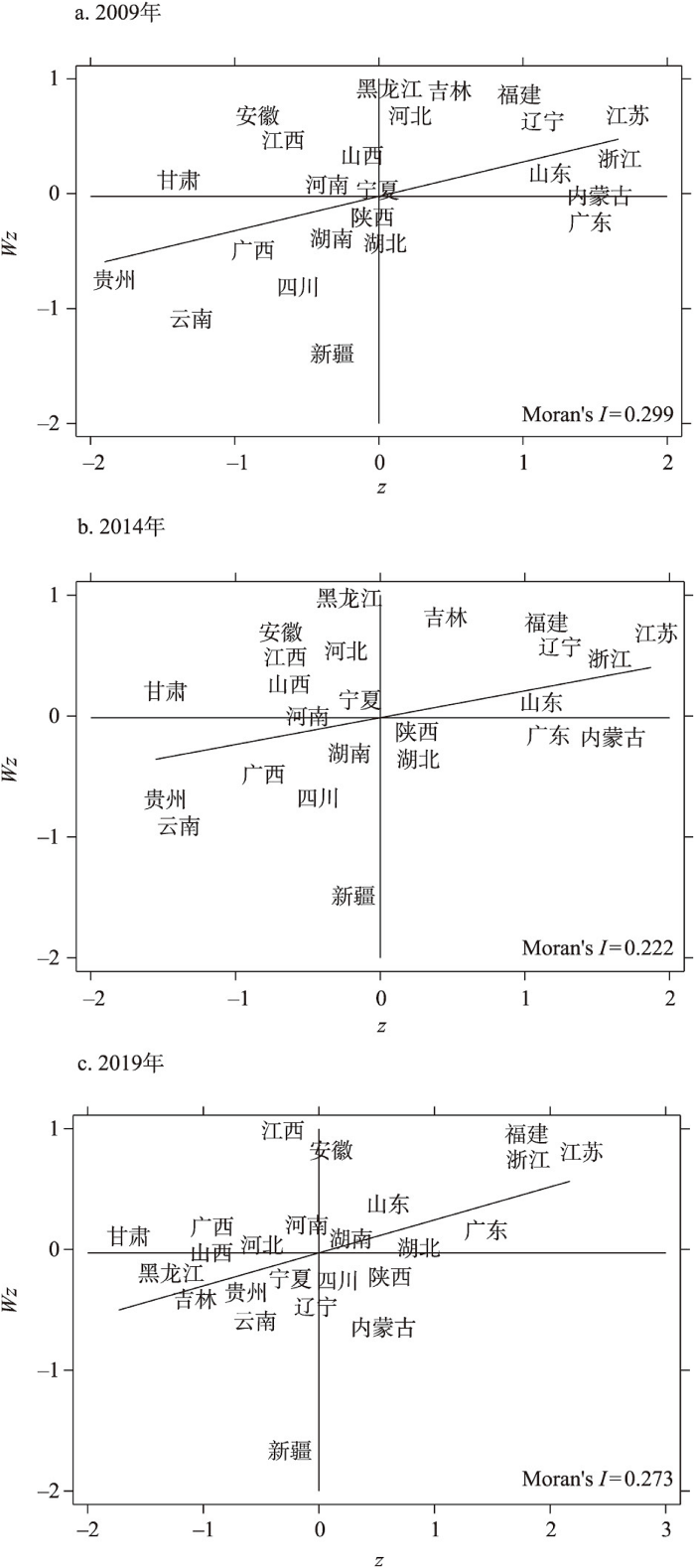
图1
图1
2009年、2014年和2019年各省份人均GDP莫兰散点图
Fig. 1
Provincial GDP per capita 2009, 2014 and 2019 Moran scatter plot
下一步进行空间杜宾模型回归分析。需要说明的是,由于本文核心解释变量为各省是否双核结构的0、1变量,如果采用固定效应模型,回归结果会自动省略该变量而无法进行后续的分析,因此为保留该变量的回归结果,本文直接采取随机效应模型进行回归。同时,为了检验空间杜宾模型是否会退化为空间自回归模型SAR或者是空间误差模型SEM,本文进行了LR检验和Wald检验。检验的原假设为空间杜宾模型会退化为空间自回归模型或者空间误差模型。如果能拒绝原假设,则需要选择空间杜宾模型进行回归分析,否则根据检验结果选择相应的模型进行回归分析。在基准回归中,无论是LR检验还是Wald检验结果都表明应使用空间杜宾模型进行回归。表6为LR检验和Wald检验的结果,表7为空间杜宾模型的回归结果。
表6 LR检验和Wald检验回归结果
Tab. 6
| 检验形式 | 检验值 | P值 |
|---|---|---|
| LR检验 | 空间自回归模型检验: 113.45 | < 0.001 |
| 空间误差模型检验: 19.49 | 0.0002 | |
| Wald检验 | 空间自回归模型检验: 139.01 | < 0.001 |
| 空间误差模型检验: 8.13 | 0.0435 |
表7 空间杜宾模型回归结果
Tab. 7
| 变量 | (1) sdm Main | (2) Wx | (3) Spatial | (4) Variance | (5) LR_Direct | (6) LR_Indirect | (7) LR_Total |
|---|---|---|---|---|---|---|---|
| dualcore | 0.239**(0.100) | 0.397**(0.167) | 1.998**(0.927) | 2.395**(1.084) | |||
| inv | 0.205***(0.027) | -0.135***(0.034) | 0.236***(0.038) | 0.410(0.272) | 0.645**(0.301) | ||
| con | -1.153***(0.148) | 1.086***(0.232) | -1.085***(0.233) | 0.685(2.083) | -0.400(2.274) | ||
| afc | 1.398***(0.401) | 2.308***(0.687) | 11.796***(4.548) | 14.104***(5.186) | |||
| gov | -1.521***(0.199) | 1.918***(0.323) | -1.152***(0.282) | 4.795*(2.536) | 3.642(2.748) | ||
| col | 11.041***(2.404) | 18.165***(3.455) | 90.731***(20.007) | 108.896***(22.620) | |||
| rho | 0.897***(0.018) | ||||||
| 样本量 | 24 | 24 | 24 | 24 | 24 | 24 | 24 |
注:*、**、***分别表示在10%、5%、1%的水平下显著;括号内数值为标准误差。
表7展示了空间杜宾模型的回归结果,空间自回归系数ρ值通过1%的显著性水平检验,通过逐个加入各变量的空间滞后项检查回归结果是否显著,最后选择固定资产投资与地区生产总值的比值inv、社会消费品零售总额与地区生产总值的比值con、政府支出与地区生产总值的比值gov作为空间滞后项。根据空间杜宾模型的回归结果可以得到,核心解释变量dual-core的直接效应为0.397,间接效应较大为1.998,总效应为2.395,直接效应、间接效应和总效应均通过了5%的显著性水平检验,表明区域双核结构对于各省份的经济发展具有明显的促进作用。实证分析结果与预期基本一致,区域双核结构由于兼顾了中心城市和门户城市的作用,对于本省中小城市的经济发展具有更加显著带动作用,同时由于门户城市的发展加大了本省内部及与其他地区的沟通交流,由此对于本地经济发展具有明显促进作用。
其他控制变量的回归结果中,固定资产投资inv对于本省的经济发展的直接效应和总效应均显著为正,表明本省的固定资产投资对于本省经济发展具有显著促进作用。社会消费品零售总额con直接效应系数显著为负,本文认为这可能和地区消费结构有关,此外随着电商及物流的不断完善,跨地区购物及消费逐渐占据重要位置,这也使得本地消费对本地经济发展影响效应减弱。实际利用外资afc对于本省的经济发展的回归结果直接效应、间接效应和总效应均为正,回归结果显著;主要原因是区域双核结构中的核心城市大部分位于沿海,对外开放程度高,实际利用外资程度可能相对于内陆城市要更好,对外开放对于区域经济发展的带动作用更加明显。政府财政支出gov对于区域经济发展的直接效应为负,间接效应为正,总效应为正但不显著;一般而言政府财政支出的影响效果依赖于财政支出的方向和投入情况,比如财政支出中的科技支出对于科技创新型企业具有正向影响,但是该项财政支出一般局限于特定的城市、特定的产业,对于其他城市及产业的发展可能并不具有促进作用。高等教育在校生人数col的回归结果无论是直接效应、间接效应还是总效应都显示出了显著的正向影响,而高等教育在校生人数col的回归结果系数较其他变量大,是因为变量反映了高等教育在校生人数占地区常住人口的总值比率,因人口基数较大、比值结果较小引致回归结果偏大。人力资本作为影响经济发展的重要因素,对于经济发展存在明显的正向影响,同时邻近区域的影响也显著为正。一般而言,大学生多会选择学校周边的区域就业,因此,相邻的区域都会成为其就业选择,相邻省份的大学生在校人数对于本省经济发展的正向影响也基本符合现实情况。
4.3 稳健性检验
4.3.1 更换权重矩阵的回归分析
表8 地理距离矩阵下Moran's I指数检验
Tab. 8
| Moran's I | 变量 | I | E(I) | sd(I) | z | P值 |
|---|---|---|---|---|---|---|
| pgdp | 0.419 | -0.004 | 0.021 | 19.758 | < 0.001 | |
| Geary's C | 变量 | c | E(c) | sd(c) | z | P值 |
| pgdp | 0.575 | 1.000 | 0.024 | -17.821 | < 0.001 |
表9 地理距离矩阵的回归结果
Tab. 9
| 变量 | (1) sdm Main | (2) Wx | (3) Spatial | (4) Variance | (5) LR_Direct | (6) LR_Indirect | (7) LR_Total |
|---|---|---|---|---|---|---|---|
| dualcore | 0.251***(0.095) | 0.371***(0.144) | 2.803**(1.376) | 3.173**(1.505) | |||
| inv | 0.220***(0.025) | 0.321***(0.046) | 2.438***(0.847) | 2.759***(0.887) | |||
| con | -1.501***(0.163) | 0.710**(0.331) | -1.824***(0.260) | -8.155*(4.635) | -9.980**(4.845) | ||
| afc | 2.303***(0.414) | 3.389***(0.746) | 25.988**(10.466) | 29.377***(11.137) | |||
| gov | -1.896***(0.184) | 2.861***(0.653) | -1.371***(0.335) | 12.742*(6.905) | 11.372(7.190) | ||
| col | 9.054***(2.556) | 13.431***(3.758) | 101.247**(41.729) | 114.677**(44.864) | |||
| rho | 0.916***(0.020) | ||||||
| 样本量 | 24 | 24 | 24 | 24 | 24 | 24 | 24 |
注:*、**、***分别表示在10%、5%、1%的水平下显著;括号内数值为标准误差。
根据表9的回归结果,在更换为地理距离矩阵之后,回归结果仍然支持基准回归的结论,无论是直接效应、间接效应还是总效应都表明,区域双核结构对于各省份的经济发展具有非常明显的促进作用。区域双核结构直接效应回归系数为0.371,间接效应为2.803,总效应的回归系数为3.173,直接效应通过了1%的显著性水平检验,间接效应和总效应均通过了5%的显著性水平检验。总体来看,回归系数略大于基准回归的回归系数。其他控制变量的回归结果与基准回归结果一致,可以认为在更换为地理距离矩阵后仍然支持基准回归结果的基本结论,回归结果稳健。
4.3.2 更换被解释变量的回归分析
本文的核心被解释变量为各省人均GDP的对数值,从人均产出的角度反映区域双核结构对于各省份经济发展的影响。稳健性检验中,核心被解释变量为各省GDP的对数值,以反映各省经济总量上的发展受区域双核结构的影响是否依然为正。此外,还将以各省人均收入的对数值以及人均工资的对数值作为被解释变量,从收入的角度衡量区域双核结构是否依然能够促进当地经济发展。结果如表10所示。
表10 更换被解释变量的回归结果
Tab. 10
| 变量 | lngdp | lnincome | lnwage | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| (1) LR_Direct | (2) LR_Indirect | (3) LR_Total | (4) LR_Direct | (5) LR_Indirect | (6) LR_Total | (7) LR_Direct | (8) LR_Indirect | (9) LR_Total | |||
| dualcore | 1.256*** (0.419) | 8.427** (3.411) | 9.683** (3.795) | 0.324*** (0.084) | 1.813*** (0.530) | 2.137*** (0.606) | 0.155** (0.064) | 0.636** (0.280) | 0.791** (0.342) | ||
| inv | 0.119*** (0.028) | 0.332 (0.257) | 0.451 (0.281) | 0.050** (0.022) | 0.509*** (0.158) | 0.559*** (0.174) | 0.075*** (0.022) | 0.309*** (0.102) | 0.384*** (0.123) | ||
| con | -1.765*** (0.179) | 2.182 (1.973) | 0.417 (2.129) | -0.085 (0.133) | -0.495 (0.772) | -0.580 (0.904) | -0.117 (0.132) | -0.496 (0.571) | -0.612 (0.702) | ||
| afc | 1.854*** (0.528) | 12.574** (5.173) | 14.428** (5.659) | -0.157 (0.393) | -0.825 (2.224) | -0.983 (2.613) | -1.344*** (0.471) | -17.423*** (4.387) | -18.767*** (4.776) | ||
| gov | -1.091*** (0.236) | -1.106 (2.812) | -2.197 (3.018) | 0.606*** (0.156) | 7.818*** (1.330) | 8.424*** (1.437) | 0.337** (0.164) | 1.368** (0.677) | 1.705** (0.835) | ||
| col | 11.973*** (2.370) | 156.116*** (24.377) | 168.089*** (25.696) | 8.950*** (2.283) | 49.363*** (11.736) | 58.313*** (13.762) | 10.589*** (2.148) | 132.125*** (11.120) | 142.714*** (11.823) | ||
| 观测量 | 264 | 264 | 264 | 264 | 264 | 264 | 264 | 264 | 264 | ||
| R2 | 0.415 | 0.415 | 0.415 | 0.526 | 0.526 | 0.526 | 0.765 | 0.765 | 0.765 | ||
| 样本量 | 24 | 24 | 24 | 24 | 24 | 24 | 24 | 24 | 24 | ||
注:*、**、***分别表示在10%、5%、1%的水平下显著;括号内数值为标准误差。
表10中前3列为以各省GDP对数值为被解释变量的回归结果,第4~6列为以各省人均收入对数值为被解释变量的回归结果,最后3列为以各省人均工资对数值为被解释变量的回归结果,限于篇幅,这里只展示了3个回归的直接效应、间接效应和总效应的结果。从回归结果可以看出,区域双核结构对于省份经济发展具有明显的促进作用。
4.3.3 去掉部分省份的回归分析
前文第三部分在进行区域双核结构的确定时,部分省份地级市的中心性和门户性并不满足聚类分析确定的高中心性和高门户性标准,这些省份包括内蒙古自治区、宁夏回族自治区、新疆维吾尔自治区、贵州省、甘肃省、云南省,因此采取了人工计算的方式确定这些区域是否属于区域双核结构。而为了剔除人为因素的影响,更精确地反映出区域双核结构的影响,本文将删掉这些省份再次进行回归,以检验剩余省份的区域双核结构是否仍然对本地经济发展具有正向促进作用。在进行了LR和Wald检验后,结果表明仍采取空间杜宾模型进行回归,回归结果如表11所示。
表11 去掉部分省份的回归结果
Tab. 11
| 变量 | (1) sdm Main | (2) Wx | (3) Spatial | (4) Variance | (5) LR_Direct | (6) LR_Indirect | (7) LR_Total |
|---|---|---|---|---|---|---|---|
| dualcore | 0.303**(0.146) | 0.555**(0.271) | 2.380*(1.265) | 2.935*(1.527) | |||
| inv | 0.303***(0.028) | -0.176***(0.034) | 0.384***(0.049) | 0.782***(0.298) | 1.166***(0.340) | ||
| con | -2.169***(0.204) | 1.839***(0.236) | -2.222***(0.293) | -0.728(1.795) | -2.950(2.024) | ||
| afc | 0.539(0.405) | 0.988(0.731) | 4.300(3.365) | 5.288(4.082) | |||
| gov | -1.047***(0.283) | 1.828***(0.419) | -0.284(0.425) | 7.385**(2.967) | 7.101**(3.304) | ||
| col | 10.463***(2.682) | 18.993***(4.499) | 80.770***(21.904) | 99.763***(25.858) | |||
| rho | 0.893***(0.018) | ||||||
| 样本量 | 18 | 18 | 18 | 18 | 18 | 18 | 18 |
注:*、**、***分别表示在10%、5%、1%的水平下显著;括号内数值为标准误差。
从表11的回归结果中可以看出,区域双核结构对于各省份的经济发展仍然具有促进作用,区域双核结构回归系数中直接效应为0.555,通过了5%的显著性水平检验,间接效应为2.380,总效应的回归系数为2.935,均通过10%的显著性水平检验。其他控制变量的回归结果中,固定资产投资、财政支出水平和高等教育在校生人数的回归系数方向与基准回归一致,回归结果也显著,社会消费品零售总额的回归系数依旧为负但是结果不显著。总体而言,与基准回归基本保持一致,可以认为在去除了部分区域后回归结果仍然支持基准回归的结论,回归结果依然稳健。
5 讨论
实证分析结果表明,总体来看区域双核结构有助于省域经济发展,但不同省份的双核城市中心性和门户性指标得分有所不同,因此应进一步区分不同区域双核结构的影响效果。同时,区域双核结构的省份由于核心城市数量增加,对于周边产业和人才的吸引力加大,那么是否有助于本地产业集聚?区域双核结构是否因人才集聚进而促进了创新水平的提高?这两个问题涉及构建新发展格局背景下供给侧改革和创新驱动战略的两个重要方面,值得进一步讨论。
5.1 南、北方地区区域双核结构的影响
本文的主要目的是研究区域双核结构对省域经济发展的影响,因此,在确定核心解释变量时只要确定各省份是否为区域双核结构进而选取0、1变量即可。而进一步区分中心性和门户性指标的数值大小对于不同区域的不同影响,更有助于根据不同的情况进行具体分析。在测度各省份地级市中心性和门户性指标得分时,可以发现南方大部分省份的地级市的中心性和门户性指标更高,因此,本文参照多数文献作法以秦岭—淮河分界线作为南、北方省份划分依据[17],同时综合考虑该分界线贯穿的一些省份,将江苏省、浙江省、安徽省、福建省、江西省、湖北省、湖南省、广东省、广西壮族自治区、四川(包含重庆)、贵州省、云南省12个省份归为南方,把山东省、河南省、山西省、陕西省、甘肃省、新疆维吾尔自治区、河北省、内蒙古自治区、辽宁省、吉林省、黑龙江省、宁夏回族自治区作为北方省份,依此进行回归的结果如表12所示。
表12 南、北方两地区的回归结果
Tab. 12
| spro | npro | ||||||
|---|---|---|---|---|---|---|---|
| 变量 | (1) LR_Direct | (2) LR_Indirect | (3) LR_Total | (4) LR_Direct | (5) LR_Indirect | (6) LR_Total | |
| dualcore | 0.683** (0.276) | 2.503** (1.112) | 3.185** (1.374) | 0.366* (0.212) | 1.059 (0.656) | 1.426* (0.859) | |
| inv | 0.508*** (0.112) | 2.733*** (0.739) | 3.241*** (0.837) | 0.238*** (0.043) | 0.375** (0.172) | 0.613*** (0.204) | |
| con | -3.052*** (0.503) | -11.339*** (3.232) | -14.391*** (3.693) | -0.849*** (0.294) | -2.505** (1.092) | -3.354** (1.363) | |
| afc | 0.497 (1.080) | 2.060 (4.287) | 2.557 (5.354) | 2.516*** (0.832) | 7.454** (3.179) | 9.971** (3.949) | |
| gov | -0.107 (0.512) | 15.326*** (3.400) | 15.218*** (3.837) | -0.688** (0.329) | 5.815*** (1.615) | 5.127*** (1.834) | |
| col | 4.972 (6.137) | 16.927 (22.435) | 21.899 (28.487) | 29.629*** (6.555) | 86.137*** (25.208) | 115.766*** (30.519) | |
| 观测量 | 132 | 132 | 132 | ||||
| R2 | 0.681 | 0.681 | 0.681 | 0.728 | 0.728 | 0.728 | |
| 样本量 | 12 | 12 | 12 | 12 | 12 | 12 | |
注:*、**、***分别表示在10%、5%、1%的水平下显著;括号内数值为标准误差。
表12中前3列展示的是南方各省份的回归结果,后3列展示的是北方各省份的回归结果。从中可以看出,虽然南北地区的回归结果均显著,但回归结果中南方地区双核结构的回归系数更大,表明区域双核结构对于南方各省份经济发展的正向影响更大。同时,南方省份区域双核结构也相对更加成熟,双核心城市的中心性和门户性指标得分更高,因此区域双核结构对于区域经济发展的正向影响更加明显。相对而言,北方各省份双核心城市的中心性以及门户性指标得分还不高,核心城市的建设尚未达到最优水平,对于区域经济发展的促进作用尚没有充分发挥出来。
5.2 区域双核结构对于产业集聚的影响
为对这一问题进行验证,本文以区位熵方法计算各省份第二、三产业的集聚度指数agg,以此作为被解释变量进行回归分析。第二、三产业集聚度计算公式为:
式中:vj为j省第二、三产业的增加值;GDPj为j省地区生产总值;v为全国第二、三产业的增加值;GDP为全国生产总值。首先计算莫兰指数,结果表明应选用空间面板数据计量方法。在进行LR检验和Wald检验后,计算出空间杜宾模型的回归分析结果(表13)。
表13 双核结构对产业集聚度影响的回归结果
Tab. 13
| 变量 | (1) sdm Main | (2) Wx | (3) Spatial | (4) Variance | (5) LR_Direct | (6) LR_Indirect | (7) LR_Total |
|---|---|---|---|---|---|---|---|
| dualcore | 0.015(0.015) | 0.048*0.026) | 0.014(0.016) | 0.037(0.023) | 0.051**(0.020) | ||
| inv | -0.009(0.006) | -0.010(0.006) | 0.002(0.001) | -0.008(0.005) | |||
| con | -0.035(0.038) | 0.167***(0.049) | -0.040(0.037) | 0.153***(0.045) | 0.113***(0.041) | ||
| afc | 0.205**(0.104) | 0.208**(0.103) | -0.037(0.025) | 0.171**(0.087) | |||
| gov | -0.132***(0.042) | -0.134***(0.042) | 0.024*(0.013) | -0.110***(0.035) | |||
| col | -0.448(0.779) | 1.695*(1.007) | -0.488(0.824) | 1.502(0.986) | 1.014*(0.535) | ||
| rho | -0.212**(0.095) | ||||||
| 样本量 | 24 | 24 | 24 | 24 | 24 | 24 | 24 |
注:*、**、***分别表示在10%、5%、1%的水平下显著;括号内数值为标准误差。
从表13的回归结果可以看出,区域双核结构对于本省第二、三产业集聚的总效应回归系数为0.051,且通过了5%的显著性水平检验。直接效应和间接效应的回归系数虽然为正但是并不显著,对此结果,首先,本文在回归时涉及的是全部第二、三产业,由于相关数据获取难度较大,未能做进一步的产业内的行业细分,因此相关结果有待分行业做进一步分析。其次,考虑到城市门户性的作用,双核结构可能更有利于制造业等产业集聚,而随着互联网产业等的发展,近年来双核结构对于传统产业的集聚效应可能会受到一定影响。因此总体来看,区域双核结构对于区域产业集聚具有一定的正向促进作用,但对于不同产业的影响存在一定的差异。
5.3 区域双核结构对于科技创新水平的影响
那么,区域双核结构是否有助于区域科技创新水平的提高?本文以各省份的专利申请数的对数值作为被解释变量进行回归分析。由于科技创新受科技研发人员和科技研发投入的影响较大,所以本文的解释变量除了基准回归中的变量外,还加入了各省份R&D从业人员集聚度aggrdper和R&D投入集聚度aggrd作为解释变量。各省份R&D从业人员集聚度aggrdper及R&D投入集聚度aggrd采用熵值法计算,公式为:
式中:aggrdj为j省R&D投入集聚度;rdj为j省R&D投入;GDPj为j省地区生产总值;rd为全国R&D投入;GDP为全国国内生产总值;aggrdperj为j省R&D从业人员集聚度指数;rdperj为j省R&D从业人员;workerj为j省从业人员总数;rdper为全国R&D从业人员;worker为全国就业人员总数。在进行莫兰指数检验以及LR检验和Wald检验之后,选择空间杜宾模型进行回归,回归结果如表14所示。
表14 双核结构对科技创新水平影响的回归结果
Tab. 14
| 变量 | (1) sdm Main | (2) Wx | (3) Spatial | (4) Variance | (5) LR_Direct | (6) LR_Indirect | (7) LR_Total |
|---|---|---|---|---|---|---|---|
| dualcore | 1.216***(0.314) | 1.352***(0.353) | 1.425***(0.429) | 2.778***(0.752) | |||
| aggrd | 0.458*(0.247) | 0.493*(0.262) | 0.517*(0.283) | 1.011*(0.539) | |||
| aggrdper | 0.790***(0.214) | 0.895***(0.229) | 0.950***(0.295) | 1.845***(0.507) | |||
| inv | 0.210*(0.119) | 0.229*(0.124) | 0.238*(0.130) | 0.467*(0.251) | |||
| con | -0.485(0.701) | -0.529(0.728) | -0.570(0.787) | -1.098(1.509) | |||
| afc | 1.522(1.949) | 1.774(2.121) | 1.950(2.338) | 3.724(4.435) | |||
| gov | 2.380**(0.963) | 4.082***(1.375) | 3.390***(0.956) | 11.400***(2.221) | 14.789***(2.381) | ||
| col | 91.881***(11.563) | 100.714***(11.427) | 105.725***(15.595) | 206.439***(22.486) | |||
| rho | 0.558***(0.045) | ||||||
| 样本量 | 24 | 24 | 24 | 24 | 24 | 24 | 24 |
注:*、**、***分别表示在10%、5%、1%的水平下显著;括号内数值为标准误差。
从表14的回归结果来看,区域双核结构对于省域科技创新水平具有促进作用,直接效应为1.352,间接效应为1.425,总效应为2.778,且均通过了1%的显著性水平检验,说明区域双核结构有助于各省份科技创新水平的提高。其他解释变量中,区域R&D人才集聚度各效应均为正,表明无论是本区域还是邻近区域的R&D人才集聚对于本区域的创新水平均有正向影响。R&D经费投入的直接效应、间接效应和总效应均促进了区域科技创新水平的提高。社会消费品零售总额和实际利用外资回归结果不显著。财政支出和高等教育在校生人数对于省域科技创新水平具有显著促进作用。
6 结论
(1)区域双核结构对于中国省域经济发展具有显著的促进作用。在本文的基准回归中,以各省份人均地区生产总值的对数为核心被解释变量,以各省份是否为区域双核结构作为核心解释变量进行回归分析。结果表明,区域双核结构对于各省份的经济发展具有明显的正向作用。本文通过更换权重矩阵、更换被解释变量和去掉部分省份的方法进行了稳健性检验,依然得出了区域双核结构对于各省份的经济发展具有促进作用的结论。
(2)区域双核结构对于南、北方地区经济发展的影响程度不同。本文分别对南、北方地区的区域双核结构省份进行回归,发现南方省份区域双核结构的回归系数要大于北方省份。这是由于南方各省份的双核心城市中心性和门户性指标得分更高,其核心城市规模及产业更强,对于区域经济发展的辐射带动性更大。相对而言,北方各省份的双核心城市的发展还有待进一步提高,对于区域经济发展的带动能力也有待增强。因此,北方各省份应更加注重核心城市的建设,尤其是对于城市中心性和门户性指标较低的省份更是如此。
(3)区域双核结构对于各省份的产业集聚具有一定的促进作用。一般而言第三产业更倾向于在核心城市选址,便于享受当地更加方便快捷的服务;第二产业倾向于在港口城市或者交通发达的城市选址,以减少运输成本。而区域双核结构给二、三产业提供了双重便利,因此可以促进产业集聚,但对于产业内不同行业的影响效果还有待更加深入的分析。
(4)区域双核结构有助于促进省域科技创新水平的提高。这是因为科技创新水平的提高需要资金、人才、设施等要素的支持,而双核结构省域中双核心城市的发展模式能够为科技创新提供更多的相关要素集聚,因此更有助于促进科技创新水平的提高。
本文分析结果的启示在于,一方面,各地在核心城市的规模及数量上存在较大差异,总体来看,与部分省会城市规模不大、辐射带动力不强的单核结构省份相比,呈双核结构特征的省份可以凭借中心城市数量及空间分布的优势在一定程度上弥补这些短板,相对来说更有助于带动当地经济发展;部分省份在实施“强省会”战略加大中心城市辐射带动能力的同时,也应注重核心城市空间布局的均衡性,一些地区有可能靠区域双核城市的带动作用得到“1+1>2”的效果。另一方面,随着城市化进程的加快,一些经济发达省份的中心城市开始出现由集聚效应向扩散效应的转变,相应表现出双核空间结构特征的省份也有所增加,如江苏等地已经呈现出较强的多中心结构的特征,这方面的动态会对中国的区域经济发展及空间格局产生深远影响,值得进一步关注和探讨。
参考文献
Study on the model of two-core space structure
双核型空间结构模式的探讨
The theoretical logic and practical strategy of the "twin cities" linkage of urban agglomeration: Taking Guangzhou and Shenzhen in the Guangdong-Hong Kong-Macao Greater Bay Area as examples
城市群“双城”联动的理论逻辑与实践策略: 以粤港澳大湾区广州、深圳为例
Applied prospect of the model of two core spatial structure
双核型空间结构模式的应用前景
Model of double-core structure and strategy of regional development in Hebei province
双核结构模式与河北区域发展战略探讨
The mathematical derivation of the model of regional dual-nuclei structure
DOI:10.11821/xb200303010
[本文引用: 1]

In order to derive the regional dual-nuclei structure by the method of building mathematical model, this paper redefines regional accessibility and establishes the formula to calculate it. Our research indicates that the present formula of accessibility measures materially the centrality of one point in a special region. So the present regional accessibility is only the regional internal accessibility. Based on this, this paper divides the regional accessibility into two parts as regional external accessibility and regional internal accessibility. The method to measure regional external accessibility is discussed in detail. The present method fails to measure regional external accessibility because it is impossible to get the value of the regional external accessibility of the gate point. We hypothesize a virtual point located outside the region to resolve the problem. Using the new concept of regional accessibility, this paper derivates the mechanism of the model of dual-nuclei structure and parameters of its existence under the hypothetical background of homogeneous plain. It is also verified that river basin is the best background for dual-nuclei structure to appear. Other spatial structure models can be derived by varying the parameters, because regional dual-nuclei structure is merely one of the spatial structure models.
区域双核结构模式的数学推导
The type of formation of dual-nuclei structure
双核结构的形成类型
Spatial coupling mechanism of dual- nuclei structure
双核结构的空间耦合机理
The rule cognition and theoretical construction of spatial pattern in China
DOI:10.11821/dlxb202112002
[本文引用: 1]

"Hu Huanyong Line", T-shaped development model, and dual-nuclei structure model can be roughly summarized as a "one-line, two-axis, and dual-nuclei" structure. They are all rule cognition and theoretical refinements on spatial pattern in China which were proposed by Chinese human geographers in different periods. "Hu Huanyong Line" is proposed based on the regular recognition of regional differences. This is the extension and expansion of geographical differentiation laws of physical geography in human geography, following the basic assumption of homogeneous regions. The discovery of the T-shaped model of Lu Dadao and the dual-nuclei structure of Lu Yuqi transcended the analytical thought of regional differentiation laws. They follow the basic assumptions of functional areas. Among them, the T-shaped model is the practical application of the point-axis system theory proposed by Lu Dadao in China. From the phenomenon perspective, the dual-nuclei structure is attached to the T-shaped development model, but subsequent research has completed the transformation from special to general. It has accomplished the whole process of scientific research in scientific discovery, mechanism analysis, mathematical derivation and practical application. Eventually, it becomes a regional spatial structure theory with strong broad applicability. From the theoretical level, "Hu Huanyong Line" based on the assumption of homogeneous region and T-shaped model based on the assumption of functional region belong to the analysis results of spatial differentiation law, but they can also be called theories. They are individual theories in geography, while the dual-nuclei structure theory belongs to a more general and applicable theory in the general scientific sense. Obviously, the trinity analysis of the "Hu Huanyong Line", the T-shaped model, and the dual-nuclei structure theory shows that, China is a country that is very suitable for regional analysis and geographical laws and theories refinement based on this. The research in this paper can provide research ideas and method references for the summary of regional spatial structure laws and theory refinement of human geography.
中国空间格局的规律认知与理论提炼
DOI:10.11821/dlxb202112002
[本文引用: 1]

胡焕庸线、“T”型模式以及双核结构,可归纳为“一线两轴双核”结构,是不同时期中国人文地理学者对于中国空间格局的规律认知和理论提炼。胡焕庸线属于自然地理学地域分异规律在人文地理学中的延伸和拓展,遵循的是均质区域的基本假设;“T”型模式和双核结构则超越了地域分异规律的分析思路,遵循的是功能区域的基本假设。其中,“T”型模式是陆大道提出的点轴系统理论在中国的实践应用。从现象看,双核结构附属于“T”型开发模式,但后继研究实现了由特殊向一般的转化,完成了科学发现、机理分析、数学推导和实践应用的全过程科学研究,成为一个普适性较强的区域空间结构理论。从理论层面而言,分别基于均质区域和功能区域假设的胡焕庸线和“T”型模式属于空间分异规律的分析结果,属于地理学中的个例性理论;双核结构则属于符合一般科学意义上的普适性较强的理论。显然,胡焕庸线、“T”型模式和双核结构三位一体的分析,一方面表明中国是一个非常适合进行区域分析并在此基础上进行地理学规律和理论提炼的国家;另一方面,本文的研究可为区域空间结构规律的总结和人文地理学理论的提炼提供研究思路和方法论角度的启迪。
The evolution and location of Guangzhou applying dual-nuclei
广州的双核结构演变及其城市发展定位分析
Economies of scale, foreign trade and the dual-core spatial structurein regional development
规模经济、对外贸易与区域双核结构模式探讨: 以山东半岛济南—青岛双核结构为例
Regional space linkage mode research in the perspective of dual-core structure: Take Lanzhou-Xining economic zone as an example
双核结构视角下的区域空间联动模式研究: 以兰州—西宁经济区为例
Measuring the potential of city location and picturing regional dual-nuclei structure with Gravity Model: Evidence from Jinan-Qingdao in Shandong province
基于引力模型的城市区位潜力测度与区域双核结构刻画: 以山东省济—青双核结构为例
Study on identification of center-gateway and opening-up pattern in Yunnan province based on dual-nuclei structure
基于双核理论的云南省中心—门户识别与对外开放布局研究
The evolution of China's regional economic theory and its future prospects
中国区域经济理论演进与未来展望
Analysis on the gateway property and gateway-city groups of China
DOI:10.13249/j.cnki.sgs.2017.03.002
[本文引用: 2]

Under the background of economic globalization, gateway cities has become the sink and jointing area of all kinds of flow, the nodes of world as well as the control center of economic system. Gateway cities play a substantial role in socioeconomic exchanges between neighboring countries and regions. In recent years, our country has been implementing the Belt and Road Initiative actively. The “Belt and Road Initiative” is and will continue to be an overall strategy of China’s all round opening-up for a long time into the future. It targets at enabling the countries along the Belt and Road to achieve economic policy coordination and carry out broader, deeper, and more efficient economic cooperation. In this process, gateway cities play an important role. So it is very meaningful to analyze the gateway property and gateway-city groups of China. From the perspective of function and location, taking 343 prefecture cities of Chinese mainland as examples, this article constructs the coupling evaluation index system about gateway city property. The evaluation system mainly contains four aspects: scale, installation level, convenience and external dependence. The main conclusions of this study are as follows: Firstly, geographically, the gateway city property indexes of China progressively diminish in scale from eastern to central and western China. There are four high value cluster in eastern region, and they are Beijing-Tianjin-Tangshan area, Yangtze River Delta, Pearl River Delta and Shandong Peninsula. But there is no obvious high value cluster in the middle western areas of China. And the gateway functions, location conditions and regional spatial structure are the main factors influencing gateway city property distribution. Secondly, based on the chart criterion and K-means cluster, we can divided all gateway cities into four grades. The number of each grade is 10, 25,70 and 238. High grade gateway cities tend to distribute along the river and coast. Lower grade gateway cities are widely distributed in the middle and west inland. Thirdly, based on the above research, we mark out 6 gateway-city groups of China, and we identified the hinterland range of them by using the field model. The hinterland range of every gateway-city groups are variable in scale, and they have formed obvious regional specialization. Lastly, we combed the relationship between the gateway city property and China's open system, and we find that they influence each other. Besides, we refined the structural figure for the main gateway of China in new period. We hope our research can provide a comprehensive measure system to measure the gateway function of city and a new perspective to cognitive the structure features of Chinese urban system.
城市门户性与中国门户群研究
DOI:10.13249/j.cnki.sgs.2017.03.002
[本文引用: 2]

基于职能与区位二元视角,构建综合评价指标体系,对2014年中国地级以上城市的门户性、门户等级体系、门户群以及门户城市的空间结构与意象进行研究,结果表明:① 中国城市门户性在地带性尺度上呈“东中西”三级递减空间格局,东部地区门户城市空间集群趋势明显,中部、西部地区缺乏明显的高值集群。② 中国门户城市划分为4个等级,高等级门户沿海、沿江、沿边指向性明显,低等级门户广泛分布于中、西部内陆地区。③ 中国门户城市可划分为辽东半岛、京津秦唐、山东半岛、长江三角洲、海峡西岸和珠江三角洲六大门户群,六大门户群的腹地范围差异较大且区域分工明显。
Regional disparity and the influencing factors of land urbanization in China at the county level, 2000-2015
DOI:10.11821/dlxb201812005
[本文引用: 1]

In the unprecedented urbanization process in China, urbanized land has expanded quickly at the same pace or even faster than the growth of the urban population. Employing both the ordinary least square and geographical weighted regression, we analyzed the spatial patterns and factors influencing land urbanization at the county level in 2000 and 2015. This analysis was assisted by land-use data for China acquired from the resource and environment data cloud platform. The research reveals the following points: (1) The annual growth rate of land urbanization experienced 2.77 percentages on average from 2000 to 2015. About 40% of the counties witnessed an annual increase of 3% or above. Land urbanization was manifested in a pattern of diffusion, which differed from the continued spatial polarization of demographic urbanization in China. (2) Geographically, the north-south differentiation of land urbanization was clearer than the east-west differentiation. And the high-value regions tended to be located to the southeast of "Hu Line". Counties surrounding those metropolitan areas were detected as hotspots of land urbanization. In general, there was a convergent trend of land urbanization among regions in China. (3) The factors of population growth, economic development, industrial structure, city/county features, and geographical location have played significant roles in the spatial disparities of land urbanization at the county level. Besides, the spatio-temporal dependence of their influences were also explored. This study on land urbanization and its influencing factors at the county level advances our theoretical and practical understandings of the new-type urbanization, urban and rural integration, and rural revitalization strategies in contemporary China.
中国县域土地城镇化的区域差异及其影响因素
DOI:10.11821/dlxb201812005
[本文引用: 1]

中国经历了史无前例的快速城镇化进程,与之相伴随的是更加迅猛的土地城镇化过程。基于2000年和2015年中国土地利用现状遥感监测数据,综合运用空间分析、多元回归和地理加权回归的方法,深入分析了中国县域土地城镇化的区域特征及其影响因素。结果表明:① 中国县域土地城镇化率年均增长2.77%,其中近40%的区县城镇化率年均增长大于3%;在空间上呈现出不同于人口城镇化的扩散趋势。② 中国县域土地城镇化的南北分异规律较东西分异更为明显。土地城镇化的高值区域始终集中在胡焕庸线的东南半壁,而围绕主要的城市群地区则形成“组团式”增长的热点区,地区间差异趋于收敛。③ 人口集聚、经济发展、产业结构、城市特性与地理区位等要素对县域土地城镇化空间分异格局的影响较为显著、稳定,各要素对土地城镇化的影响均具有明显的时空依赖特征。分析揭示县域土地城镇化的时空特征及其动力机制,对于科学认识新型城镇化和实施城乡融合、乡村振兴战略,具有重要的理论价值与现实意义。
Increasing returns and economic geography
DOI:10.1086/261763 URL [本文引用: 1]
回报增加与经济地理
Geographic distances, input-output linkages and agglomeration
地理距离、投入产出关系与产业集聚
Principles of Economics
经济学原理