EN中文

地理学报 >

2024 , Vol. 79 >Issue 8: 1961 - 1977

DOI: https://doi.org/10.11821/dlxb202408005

人口与城市研究

基于TD-GNNWR的武汉市房价因子空间非平稳性研究

  • 吴森森 ,
  • 丁佳乐 ,
  • 严成 ,
  • 陈奕君 ,
  • 杜震洪
展开
  • 浙江大学地球科学学院，杭州 310058
杜震洪(1981-), 男, 浙江衢州人, 教授, 主要从事时空大数据与人工智能等研究。E-mail:

吴森森(1991-), 男, 浙江文成人, 副研究员, 主要从事时空大数据与人工智能等研究。E-mail:

收稿日期: 2023-02-27

  修回日期: 2024-02-02

  网络出版日期: 2024-08-06

基金资助

国家自然科学基金项目(42001323)

国家重点研发计划(2021YFB3900902)

浙江省重点研发计划项目(2021C01031)

收起

Spatial non-stationarity assessments of housing prices in Wuhan based on a TD-GNNWR model

  • WU Sensen ,
  • DING Jiale ,
  • YAN Cheng ,
  • CHEN Yijun ,
  • DU Zhenhong
Expand
  • School of Earth Science, Zhejiang University, Hangzhou 310058, China

Received date: 2023-02-27

  Revised date: 2024-02-02

  Online published: 2024-08-06

Supported by

National Natural Science Foundation of China(42001323)

National Key R&D Program of China(2021YFB3900902)

Provincial Key R&D Program of Zhejiang(2021C01031)

Fold

摘要

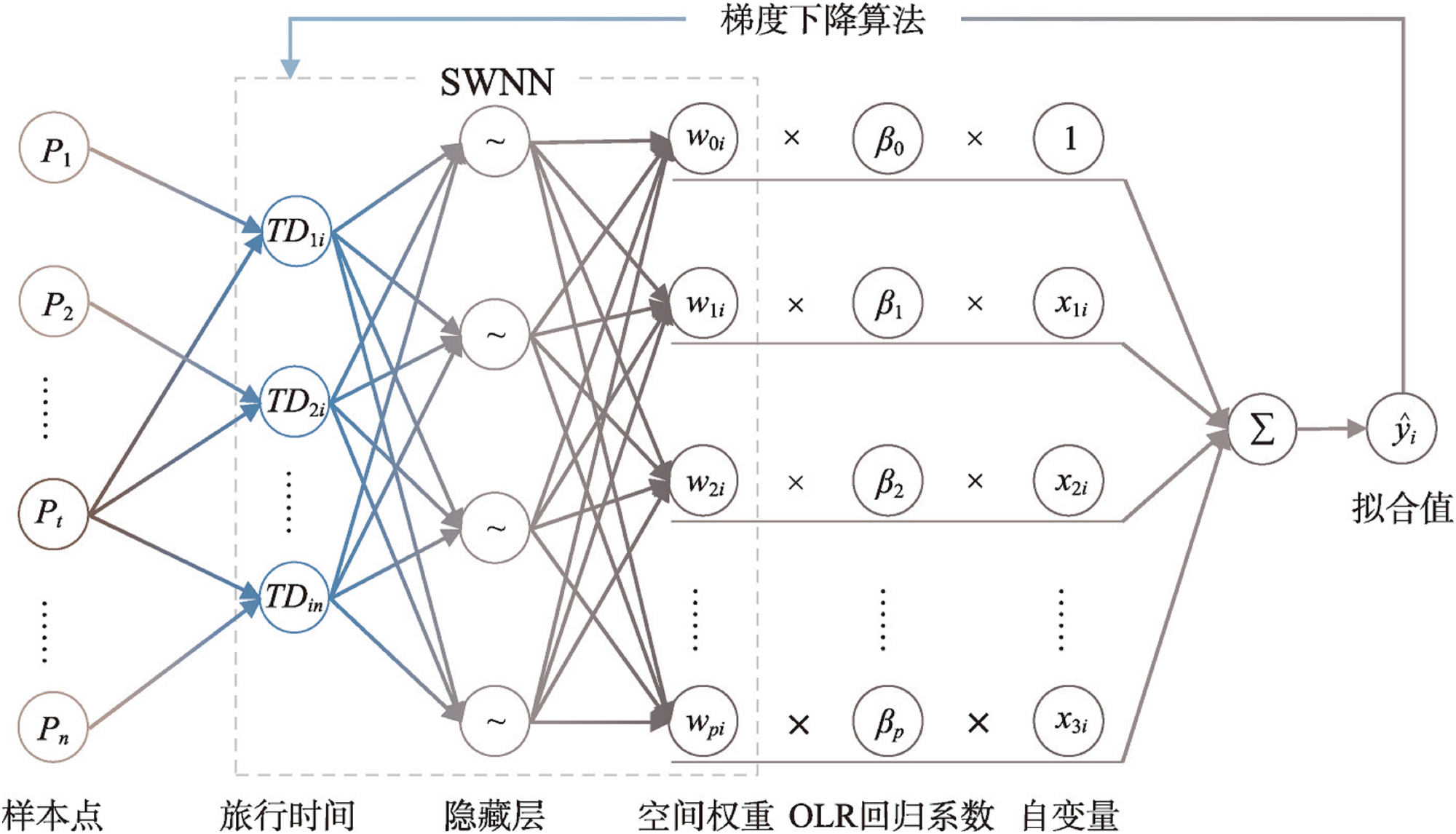
城市住房价格与其影响因子间的回归关系具有显著的空间非平稳性和复杂的非线性特征。针对传统欧式距离难以有效描述房价建模的空间邻近性、经典地理加权回归（GWR）模型难以拟合复杂非线性特征等问题，本文采用出行时间（TD）作为空间距离度量方法，并引入空间加权神经网络建立了一种基于出行时间的地理神经网络加权回归（TD-GNNWR）方法，进而构建了基于TD-GNNWR的城市房价估算模型。在武汉市2019年二手房数据的建模中，TD-GNNWR模型相比GWR模型拟合精度提升16%，且更精确地捕获了局部空间非平稳特征，可以更好地解释影响因子对武汉市房价的作用机制及城市区划导致的空间差异。

关键词： 空间非平稳性; 出行时间; 地理神经网络加权回归; 住房价格; 武汉市

本文引用格式

吴森森 , 丁佳乐 , 严成 , 陈奕君 , 杜震洪 . 基于TD-GNNWR的武汉市房价因子空间非平稳性研究[J]. 地理学报, 2024 , 79(8) : 1961 -1977 . DOI: 10.11821/dlxb202408005

Abstract

Urban housing prices are influenced by various factors, encompassing macroeconomic conditions, urban planning strategies, and the specific characteristics of housing. These elements play a crucial role in shaping urban planning and development. Nonetheless, the regression analysis depicting the interplay between urban housing prices and their influencing factors reveals significant spatial non-stationarity and intricate nonlinear characteristics. Addressing the limitations of Euclidean distance in delineating spatial proximity for housing price modeling and the challenges encountered by the geographically weighted regression model (GWR) in capturing complex nonlinear features, this study introduces travel duration (TD) as a spatial distance metric and integrates it with a spatially weighted neural network to establish a geographically neural network weighted regression model with travel duration (TD-GNNWR) to estimate housing prices. In an empirical experiment using 2019 second-hand house data in Wuhan, the TD-GNNWR model demonstrates a 16% enhancement in fitting accuracy compared to the GWR model. The TD-GNNWR model notably enhances accuracy within sparsely sampled regions and better mimics their spatial distribution. Moreover, it adeptly captures spatial non-stationarity, offering a more precise elucidation of factors influencing housing prices in Wuhan and the resultant spatial discrepancies stemming from urban zoning. Our findings underscore the comprehensive impact of various factors on housing prices in Wuhan, such as building characteristics, neighborhood attributes, and transportation accessibility. Factors like greening rates, property fees, proximity to primary schools, universities, and public transportation exert substantial influence on housing prices in Wuhan, with varying directions and strengths across different areas, signifying clear spatial differentiation. The TD-GNNWR model clearly elucidates the mechanisms underlying housing price determinants while illustrating the inherent spatial non-stationarity, which is beneficial for urban planning departments and real estate managers in policy formulation, macro-control, urban planning, and investment decision-making. This work can also serve as a valuable reference for tackling challenges in urban analysis and modeling, thereby enriching methodologies within real estate research.

Key words： spatial non-stationarity; travel duration; geographically neural network weighted regression; housing price; Wuhan

1 引言

住房价格在指导城市规划和发展中具有重要作用，尤其是在中国，住房商品化的实施和城市化的深入给房价带来了较大的不确定性。近年来住房价格在市场作用下一路走高，带来了居民消费意愿降低[1-2]、贫富差异加大[3]等问题，不利于经济良性循环和社会主义和谐社会的构建。2023年国务院政府工作报告指出，要支持房地产更好地健康发展、优化房地产行业结构、保证社会稳定和持续发展，为分析理解房价影响因子、解析其内在驱动提出了更高要求。
以往研究表明，影响房价的因素主要包括宏观经济环境背景、城市规划、住房自有特征属性等多个方面[4⇓⇓-7]。价格特征模型（Hedonic Price Model, HPM）[8-9]是一种被广泛使用、可解释性较好的房地产价格建模研究方法，其认为房屋价值由其多个属性和特征的效用所共同决定[10]。由于社会经济发展的地域差异性，住房价格与其所在城市的空间特征密切相关，呈现出极强的空间差异，房屋属性和特征的实际效用也具有显著的空间非平稳性。例如，房价整体上随着离城市中心的距离增加而降低，交通、绿化、医疗、教育和楼盘开发定位等因素对房价的作用程度在空间上也具有差异性[11]。
为刻画房价影响因子的空间非平稳性，众多研究引入地理加权回归（Geographically Weighted Regression, GWR）方法[12]建立了不同城市的房价估算模型。例如，张金亭等基于GWR模型研究环渤海城市群的房价，并对各城市房价是否存在泡沫、是否存在上升潜力等进行了定量评价[13]。周冉利用GWR模型刻画了东北地区40个地级市的房价时空演变格局，分析了地理区位、社会经济、财政政策在不同时期对房价的影响[14]。徐丹萌等基于GWR模型对沈阳市住房价格进行分析，绘制了住房价格视角下的沈阳市城市空间结构，勾勒了不同城市功能区的空间分布情况[15]。王秀兰等从城市职能分异的角度对武汉市房价进行分析，利用GWR模型对不同城市职能与房价的关系进行了探究，给出了城市发展的具体建议[16]。Osland等结合GWR模型与特征价格模型，将空间自相关性与空间变量引入挪威西南部8个城市的房价建模，证明空间变量对房价建模的显著改进[17]。Liu等使用GWR模型对珠海市的房价进行以社区为单元的局部建模，探究了建筑年龄、兴趣点（POI）距离等因素对社区内房屋价格的影响，为地方政府的社区治理提供了参考[18]。
虽然GWR模型在建立城市房价的空间非平稳关系研究中表现出较强的适用性，但对复杂非线性特征的拟合能力依然有限[19]。许多学者借助于近年来发展迅速的人工智能方法，利用其极强的非线性拟合能力对房价进行建模，取得了更优的估算精度[20-21]。不过有研究指出，基于神经网络构建的房价估算模型，由于忽略了回归关系的空间非平稳特征，获得的房价空间分布往往不合理，且建立的回归关系也不具备可解释性，限制了其在房价预测和其他社会问题方面的实际价值[22]。近年来基于空间加权的地理学思想，Du等提出了一种结合多元线性回归和神经网络的地理神经网络加权回归（Geographically Neural Network Weighted Regression, GNNWR）模型[23]。该模型构建了一种空间加权神经网络（Spatially Weighted Neural Network, SWNN），利用神经网络强大的学习能力，可以有效地解算地理要素回归关系中的空间非平稳性和复杂非线性特征[24-25]。Wang等基于GNNWR模型构建了深圳市的房价估算模型，取得了比GWR模型更高的房价拟合精度，且影响因子回归系数的空间分布表现出更强的解释能力[19]。此外，以欧式空间距离为代表的空间邻近性表达是空间回归关系建模的输入基础[26-27]。现有研究发现不同的空间距离计算方法有其适用范围，选择合适的空间距离表达能够提升GWR模型的求解精度，有助于挖掘地理现象中的空间非平稳特征[28-29]。因此，针对城市房价的空间分异特征选取合适的空间距离表达方法，也是提高房价数据空间非平稳性拟合精度的有效途径。例如，Lu等建立了基于非欧式空间距离的GWR模型，在伦敦房价的估算研究中取得了更优的拟合性能[30]。
为解决城市住房价格影响因子空间非平稳性建模问题，本文提出了一种基于出行时间的地理神经网络加权回归（Travel Duration GNNWR, TD-GNNWR）模型。该模型采用出行时间作为GNNWR的输入，可以更充分且准确地度量观测点之间的空间距离，并借助于SWNN出色的非线性拟合能力实现空间非平稳权重的精确解算。以武汉市住房价格建模为例，建立了基于TD-GNNWR的房价估算模型，通过多组对比实验验证了该模型的优越性能，并精细刻画了武汉市住房价格影响因子的作用机制及其空间差异。

2 方法

2.1 基于出行时间的地理神经网络加权回归（TD-GNNWR）方法

借鉴GWR模型的空间加权思想，GNNWR利用深度神经网络对非线性问题的拟合能力来解算回归关系的空间权重，从而实现了空间非平稳性的精确建模[23,26,31 -32]。GNNWR的公式为：
y i = w 0 u i ,   v i × β 0 + ∑ k = 1 p w k u i ,   v i × β k x i k + ε i           i = 1 ,   2 ,   ⋯ ,   n
式中： u i ,   v i表示二维平面中点i的位置坐标； β 0和 β k是普通线性回归（Ordinarily Linearity Regression, OLR）的回归系数； w 0 u i ,   v i代表 β 0的非平稳权重； w k u i ,   v i代表 β k的非平稳权重。令 β 0 u i ,   v i = w 0 u i ,   v i × β 0，且 β k u i , v i = w k u i ,   v i × β k，则 β 0 u i ,   v i和 β k u i ,   v i是GNNWR的空间回归系数，与GWR模型的表达式保持一致。
GNNWR使用空间非平稳矩阵 W u i ,   v i表示待估计点i处的空间权重，具体形式为：
W u i ,   v i = w 0 u i ,   v i 0 0 0 0 w 1 u i ,   v i 0 0 0 0 ⋯ 0 0 0 0 w p u i ,   v i
针对空间权重的解算，GNNWR以待估计点i到n个样本点的距离为输入，构建如下形式的空间加权神经网络（SWNN）：
W u i ,   v i = S W N N d i 1 ,   d i 2 ,   ⋯ ,   d i n T
式中： d i 1 ,   d i 2 ,   ⋯ ,   d i n表示待估计点i到n个样本点之间的空间距离向量。通过空间加权神经网络SWNN可以得到点i处的权重矩阵 W u i ,   v i，进而求解出 β 0 u i ,   v i、 β k u i ,   v i、yi在各样本点处的估计值。
此外，空间距离表达的准确性和充分性是精确描述空间非平稳性的重要基础，选取合适的空间距离能够提升空间模型求解的精度[27,33 -34]。地理坐标计算得到的欧式距离（Euclidean Distance, ED）较好地衡量了几何空间中的位置距离，但是在现实世界中，受到自然景观和人造地物的约束，人员和物资的流通等往往难以直接采用欧式距离，而需要借助于道路网络等信息，为此形成了不少非欧氏距离的度量方法[28,35 -36]。出行时间（Travel Duration, TD）[37]是一种较为常用的非欧式距离表达方式，通过对路网路径的实际通行时间进行求和运算所得。出行时间考虑了自然要素、人造地物、交通环境等因素的影响，在城市环境中具备更充分、更准确的空间距离表达能力。
因此，本文将出行时间作为GNNWR模型输入，提出了基于出行时间的GNNWR模型（TD-GNNWR）进行房价建模。TD-GNNWR的空间权重矩阵计算方式为：
W u i ,   v i = S W N N τ i 1 ,   τ i 2 ,   ⋯ ,   τ i n T
式中： τ i 1 ,   τ i 2 ,   ⋯ ,   τ i n表示待估计点i到n个样本点之间的出行时间向量。
基于SWNN生成的空间权重矩阵，可对待估计点i进行加权回归，得到该点的拟合值。整个TD-GNNWR模型的求解过程如图1所示。
图1 TD-GNNWR模型求解过程

注：“~”代表神经网络的隐含层，层数大于等于1。

Fig. 1 Solution process of TD-GNNWR model

2.2 对照模型

本文采用OLR和GWR方法作为对照模型。其中OLR是一种常用的全局性统计分析方法，该模型认为因变量是若干自变量的线性组合，即：
y = X β + ε
通常使用普通最小二乘法估计模型的回归系数：
β ^ = X T X - 1 X T y
GWR模型由OLR扩展而来，基于局部加权回归的思想，用空间位置变化的参数来量化表征空间关系中的非平稳性[12,38⇓⇓ -41]。GWR的公式为：
y i = β 0 u i ,   v i + ∑ k = 1 p β k u i ,   v i x i k + ε i           i = 1 ,   2 ,   ⋯ ,   n
通常采用加权最小二乘法计算GWR模型的回归系数，目标函数如下：
m i n ∑ j = 1 n w j ( u i ,   v i ) y j - β 0 u i ,   v i - ∑ k = 1 p β k u i ,   v i x j k 2
空间权重 w j u i ,   v i = w i j，其计算方法可以抽象为以下形式[26]：
w i j = f k e r n e l d i j
式中： d i j表示样本点i与i之间的空间距离； f k e r n e l表示权重核函数。

3 数据处理与实验设计

3.1 数据处理与分析

3.1.1 研究区域与数据获取

武汉市是湖北省的省会城市，位于长江中游，江汉平原东部。由于武汉地处汉江和长江的交汇处，亚热带季风的湿润气候带来了丰富的降水，武汉城区被众多河流、湖泊和池塘所分割，导致真实的地理邻近性与直线距离差异较大。本文选取武汉市作为研究区域，以更充分地表达不同距离度量对模型拟合精度的影响，进而检验TD-GNNWR方法的有效性。
武汉市房价数据为从安居客网站①(① 参见网址： https://wuhan.anjuke.com。)获取的2019年二手房交易信息，通过数据清洗剔除异常数据以及别墅、公寓等特殊住房类型。为避免个体住宅带来的数据噪声和样本重复的问题，以小区为单位聚合房价样本，计算单位均价，并匹配物业费、容积率、绿化率等信息，最终得到968个样本小区（图2）。样本点主要集中在城市中心地区和郊区地铁沿线；江岸区、江汉区、硚口区、汉阳区、武昌区和洪山区在用地规划中以居住用地为主，所得样本小区的分布亦较多；由于长江穿城而过，样本点被分割为江北和江南两部分。
图2 2019年武汉市房价样本点分布

注：数据来源于武汉市自然资源和规划局“规划一张图”(http://whonemap.zrzyhgh.wuhan.gov.cn:8020)。

Fig. 2 Sample point distribution of house prices in Wuhan in 2019

本文模型采用的欧式距离、出行时间均借助于高德开放平台提供的Web服务进行计算，主要调用其基于路径规划功能② (② 参见网址： https://lbs.amap.com/api/webservice/guide/api/direction。)的Web服务接口。对于TD-GNNWR空间权重计算输入的出行时间，需要计算任意两个小区之间的通勤时间。考虑到小区之间几乎不会毗邻，而且大部分小区之间相距较远，因此假设小区之间的通勤采用自行驾车作为出行方式，同时为了更大程度地考虑交通拥堵情况而将出发时间设定为早高峰8时，再利用高德开放平台规划驾车路径，得到通勤时间作为出行时间。

3.1.2 房价影响因子选择

综合已有研究，本文从小区建筑特征、邻里特征、交通设施可达性3个方面选取房价影响因子进行建模[11,16,42 -43]。小区建筑特征方面选取容积率、绿化率、物业费3个因子；邻里特征方面选取公园、商场、小学、中学、大学5个因子；交通设施可达性方面选择公交站、地铁站2个因子；其中邻里特征和交通设施可达性方面的因子均以到最近POI的距离为量化方式。本文所用到的房价影响因子变量如表1所示。
表1 房价及其影响因子的选择与描述

Tab. 1 Selected factors of house prices and their descriptions

特征分类 变量名 变量表示 单位
因变量 住房价格 小区住房的平均单价(Price) 元/m2
建筑特征 容积率 小区建筑面积与建筑用地面积的比率(FAR) -
绿化率 小区绿化面积与建筑用地面积的比率(GR) -
物业费 小区业主所需缴纳的物业费(PF) 元/m2·月
邻里特征 公园距离 小区几何中心到最邻近公园的距离(PD) m
商场距离 小区几何中心到最邻近商场的距离(MD) m
小学距离 小区几何中心到最邻近公立小学的距离(PSD) m
中学距离 小区几何中心到最邻近公立高中的距离(HSD) m
大学距离 小区几何中心到最邻近大学的距离(UD) m
交通设施可达性 公交站距离 小区几何中心到最邻近公交站的距离(BD) m
地铁站距离 小区几何中心到最邻近地铁站的距离(SD) m
为降低数据中的异方差性、减小各个变量的绝对极值影响，将各变量均取自然对数，并对选取的10个影响因子计算各因子的方差膨胀系数（Variance Inflation Factor, VIF）作为共线性检验，得到的结果如表2所示。各个变量的VIF值均接近1，远小于10，可见各自变量间的多重共线性现象较弱，说明选取的10个影响因子适合进行回归分析。
表2 影响因子的方差膨胀系数

Tab. 2 Variance inflation coefficients of influencing factors

变量名 PF GR FAR SD BD
VIF 1.261 1.218 1.522 1.329 1.130
变量名 PD MD PSD HSD UD
VIF 1.160 1.070 1.330 1.458 1.225

3.2 实验设计

为避免模型训练中可能出现的过拟合问题并充分利用数据集内的信息，本文采用10折交叉验证（10-fold Cross Validation）方法进行实验：先在总体样本中划分出测试集、交叉验证集两个部分，然后把交叉验证集再划分为10组，作为9组训练集和1组验证集；其中训练集用于对模型进行训练，验证集用于在训练学习的过程中对模型性能进行评价，测试集则用于对最优训练模型泛化能力的测试。实验的总体样本数量为968，随机取其中30%作为测试集共146条数据，剩余70%的样本作为交叉验证集共822条数据。每轮交叉验证实验中，交叉验证集又分为训练集739条数据和验证集83条数据。交叉验证集和测试集在空间上的分布如图3所示。
图3 数据集划分空间分布

Fig. 3 Dataset division and spatial distribution

通过控制空间回归方法、距离表达方法的不同，组合得到多个对比实验组（表3），以验证空间回归方法和距离表达方法对空间非平稳性建模的影响。在空间回归方法层面，设计了OLR、GWR、GNNWR 3种。同时，针对GWR的不同核函数类型，设计了固定型Gaussian（GWR-AFG）、自适应型Bi-square（AAB）2种较为常用的GWR模型。在空间权重约束的距离类型方面，则有欧式距离（ED）与出行时间（TD）2种。
表3 对比实验设计表

Tab. 3 Comparative experiments

模型表示 模型类型 核函数类型 空间距离类型
OLR OLR - -
ED-GWR-AFG GWR 固定的高斯核函数(Fixed Gaussian) ED
ED-GWR-AAB GWR 自适应的双二次核函数(Adaptive Bi-square) ED
TD-GWR-AFG GWR 固定的高斯核函数(Fixed Gaussian) TD
TD-GWR-AAB GWR 自适应的双二次核函数(Adaptive Bi-square) TD
ED-GNNWR GNNWR - ED
TD-GNNWR GNNWR - TD
在模型精度评价指标方面，选取决定系数R2、均方根误差（RMSE）等指标及拟合结果的空间分布等进行分析评价。

4 实验结果与分析

4.1 房价建模的精度评价

本文通过对OLR、GWR、GNNWR等方法进行10折交叉验证的对比实验，充分比较不同的模型、不同的空间距离表达在拟合以及预测住房价格的差异，所涉及的7组实验的性能指标如表4所示。
表4 OLR、GWR、GNNWR模型的房价建模结果

Tab. 4 House price modeling results for OLR, GWR, and GNNWR models

模型 训练集 测试集
R2 RMSE F1 p值 带宽 R2 RMSE
OLR 0.436 0.251 - - - 0.379 0.245
ED-GWR-AFG 0.636 0.200 0.705 0.010 7108 0.410 0.239
ED-GWR-AAB 0.659 0.194 0.668 0.010 370 0.600 0.196
TD-GWR-AFG 0.676 0.189 0.666 0.010 7885 0.613 0.193
TD-GWR-AAB 0.683 0.186 0.645 0.010 385 0.688 0.176
ED-GNNWR 0.708 0.178 0.421 0.010 - 0.683 0.175
TD-GNNWR 0.737 0.171 0.368 0.010 - 0.724 0.163
从各回归模型对实际值的拟合性能来看，可分为3个层次：OLR模型的效果最差，R2仅为0.43；GWR系列模型的效果相比OLR有明显提升，R2在0.65左右，相比OLR提升约50%，且自适应Bi-square类型的核函数比固定型的Gaussian类型核函数表现稍好；GNNWR模型的效果则进一步提升，R2达到了0.7以上，相比OLR提升约60%，相比GWR系列模型提升约10%。对比GWR和GNNWR模型中使用欧式距离与出行时间的差异，可见出行时间的拟合性能表现优于欧式距离。对于GWR-AFG模型，出行时间相比欧式距离将R2从0.636提升到0.676；对于GWR-AAB模型，出行时间将R2从0.659提升到0.683；对于GNNWR模型，出行时间则将R2从0.708提升到0.737。
相比传统的ED-GWR-AFG模型，TD-GNNWR模型的R2提升了16%（0.636~0.737），说明TD-GNNWR模型在对实际值的解释能力上有较大优势；RMSE降低了17%（0.2~0.171），说明TD-GNNWR模型可以显著地降低拟合值与实际值之间的偏差，具有较好的拟合精度。

4.2 房价拟合结果的空间形态分析

空间非平稳性假设检验F1[23]在GWR和GNNWR系列模型上的检验结果表明，武汉市房价数据具有显著的空间非平稳性。鉴于此，拟合结果在空间上的分布效果亦是重要的评价指标。表5统计了不同模型对房价拟合结果的平均相对误差。TD-GNNWR模型在各区的相对误差均小于其他模型，表现出出色的拟合能力。新洲区、汉南区和黄陂区的样本点数量较少、且离其他区的样本点距离较远，导致4个模型在这些区域的拟合结果均存在较大的误差，此时TD-GNNWR由于使用出行时间作为样本点间空间邻近性的度量，可以更准确地选择邻近点构建回归关系，从而实现相比其他模型更精确的回归结果。
表5 不同模型在武汉各区拟合结果的平均相对误差(%)

Tab. 5 Mean relative errors of fitting results of different models in Wuhan districts (%)

OLR TD-GWR-AAB ED-GNNWR TD-GNNWR
新洲区 0.83 4.20 2.41 2.02
汉南区 0.76 4.36 2.55 1.88
黄陂区 1.33 1.63 1.63 1.58
江岸区 1.64 1.58 1.55 1.48
青山区 1.86 1.53 1.43 1.41
洪山区 1.45 1.52 1.45 1.38
江汉区 1.40 1.31 1.49 1.32
武昌区 1.75 1.39 1.35 1.25
硚口区 1.34 1.27 1.24 1.19
江夏区 1.30 1.54 1.16 1.10
东西湖区 1.58 1.26 0.90 0.97
蔡甸区 1.18 1.36 1.00 0.93
汉阳区 1.47 1.09 1.03 0.87
对房价的真实值与拟合值取自然对数并插值，得到的武汉市连续的房价空间分布情况（图4），可见武汉地区的房价具有明显的空间自相关性和空间异质性。在全市范围内，房价表现出中心市区高、周围郊区低的总体趋势；武昌区、江汉区、汉阳区和江岸区的武汉三镇和旧租界区域表现为房价热点地区。OLR（图4b）和GWR（图4c）模型能大致地拟合房价的空间分布情况，但是在样本稀疏的市郊区域和空间异质性明显的市中心区域拟合结果较差，丧失了很多局部的变化细节，出现了较为明显的高值低估和低值高估现象，反映出OLR模型和GWR模型对空间非平稳性的描述不够精确、拟合结果平滑化的问题。GNNWR模型（图4d）在研究区域内的房价拟合值的数值大小、空间分布均与真实值较为接近，说明GNNWR模型对住房价格的空间分布规律、空间非平稳特征具有更高的刻画能力，优于OLR和GWR模型。
图4 武汉市不同模型的房价拟合效果空间分布

Fig. 4 Spatial distribution of house price fitting results of different models in Wuhan city

4.3 房价影响因子的空间形态分析

在对自变量和因变量进行标准化后，回归建模得到的标准化回归系数可以反映各影响因子对房价的作用情况：系数的符号代表影响因子对房价的作用方向；系数的绝对值大小反映了影响因子对房价的作用效果。TD-GNNWR模型的标准化回归系数分布情况如图5所示，选取的10个影响因子中，容积率和商场对房价的影响较小；公园、中学对房价具有中等程度的影响；绿化率、物业费、小学、大学、公交和地铁对房价的影响程度较大。同时，发现除容积率因子外，其余因子的回归系数分布范围均较大，基于已有研究的检验方法[23,44]，对回归变量的空间非平稳性和空间自相关性进行了检验，以探究因子对房价的作用效果是否具有空间特征，其结果如表6所示。9个影响因子的回归系数均在99%置信区间上通过了相关指标的F2检验和Z检验，说明影响因子对房价的作用效果具有显著的空间非平稳性和空间自相关性。
图5 TD-GNNWR模型标准化回归系数分布

Fig. 5 Distribution of standardized regression coefficients for the TD-GNNWR model

表6 TD-GNNWR模型回归变量的空间非平稳性的F2检验和空间自相关性的Moran's I 指标

Tab. 6 F2 test for spatial nonstationarity and Moran's I indicator for spatial autocorrelation of regressor variables in the TD-GNNWR model

回归变量 空间非平稳性 空间自相关性
F2 p值 Moran's I p值
绿化率 13.05 0.001* 0.9289 0.001*
物业费 344.54 0.001* 0.9255 0.001*
公园距离 42.31 0.001* 0.9112 0.001*
商场距离 44.18 0.001* 0.9156 0.001*
小学距离 22.12 0.001* 0.8905 0.001*
中学距离 28.51 0.001* 0.9224 0.001*
大学距离 46.76 0.001* 0.9050 0.001*
公交站距离 37.56 0.001* 0.9279 0.001*
地铁站距离 48.66 0.001* 0.8401 0.001*

注：*表示在99%的置信区间上显著。

本文建立了1 km×1 km的网格，对绿化率等8个对房价影响较为明显、系数分布范围较大的因子的系数进行聚合平均，并基于聚合后的格网绘制LISA聚集图（图6~图8），从而进一步地探究影响因子对房价的作用情况。
图6 武汉市建筑特征因子的空间形态

Fig. 6 Spatial patterns of structural factors in Wuhan city

图7 武汉市邻里因子的空间形态

Fig. 7 Spatial patterns of neighborhood factors in Wuhan city

图8 武汉市交通设施可达性因子的空间形态

Fig. 8 Spatial patterns of transportation accessibility factors in Wuhan city

4.3.1 建筑特征因子的空间形态分析

在研究区域范围内，绿化率因子的系数以正值为主（图6a），其中，江岸区、江岸区、武昌区等中心区域绿化率的回归系数出现明显的高—高集聚情况，由于市中心区域的小区建造时期普遍较早，住宅建设以功能性为导向，对绿化条件的投入较少，而绿化率较高的小区多为定位较高的商业住宅，导致在该区域绿化率对房价呈现出较高的正向作用。在江夏区、蔡甸区等新建设城区，由于住宅本身较新，绿化率普遍较高，且城市外围地区生态环境较好、住宅内的绿化率对生活质量的影响相对更小，该区域绿化率对房价的影响较弱，回归系数表现出低—低集聚的情况。
物业费因子的系数均为正值且绝对值较大，说明物业费与房价之间存在正向关联，且房价受物业费影响较大。同时，物业费的回归系数亦表现出明显的空间自相关和非平稳性（图6b），长江北岸呈现低—低集聚状态、南岸则以高—高集聚为主。长江北岸小区以老小区、农村回迁小区为主，以政府主导和社会自治为主要社区治理模式[45]，物业对房价的作用相对较弱；南岸多为开发年代较近、主要面向光谷新城等高新区的高收入人才的高级住宅，一般采用市场主导模式雇佣专业物业公司提供高质量的物业服务，物业费也会相对较高，对房价的影响亦更大。

4.3.2 邻里特征因子的空间形态分析

邻里特征因子的空间形态如图7所示，由于邻里特征因子采用到最近POI点的距离作为量化方式，回归系数多为负数，说明离POI越远、房价受到的负向影响越大；同时，不同于建筑特征因子的空间自相关性，邻里特征因子的低—低集聚的空间自相关说明该区域的房价受对应因子影响较大，高—集聚的空间自相关说明对应因子的影响较小。
从公园距离因子来看，在城市中心—东湖沿线区域，回归系数在较小的正值和负值间波动，并表现出不显著或高—高集聚的空间特征（图7a），说明由于该区域公园密度较高、公园可达性好、服务人口数量大[46-47]，公园绿地资源较为充足，房价受公园因子的影响较小。
小学距离因子的回归系数绝对值普遍较高，说明研究区域内房价与离最近小学的距离有较强的关联性（图7b）。在江岸区南部、武昌区、洪山区和江夏区部分区域，回归系数呈现为低—低集聚，这些区域的小学密度相对较低、学区划分面积较大[48]，因此在同样的学区条件下，离小学距离更近的住宅对有学龄儿童的家庭更具吸引力，导致房价受小学距离因子的影响更强。
相比小学因子，中学和大学距离因子回归系数的绝对值更小。考虑到中学升学由摇号和直升两部分构成，中学“学区”概念较小学不明显，中学对房价的影响作用也相对较弱；同时，大学主要通过提供绿地、运动场所等公共服务[49]间接地影响房价，作用强度有限。中学因子在空间形态上亦与小学有差异，在三环内呈现大面积的不显著或高—高集聚；而仅在中学密度较低的光谷、车谷新城内表现为低—低集聚（图7c）。类似地，大学因子的回归系数也仅在高等院校分布较少、公共服务相对缺乏的武汉市西北方向上呈现低—低集聚（图7d）。

4.3.3 交通设施可达性因子的空间形态分析

如图8所示，2种交通设施可达性因子具有类似的空间形态，在武汉主城和光谷新城等地区，回归系数呈现高—高集聚模式，交通设施可达性对房价的影响较小。这些地区开发建设时间较早、发展较为成熟、城市功能较为完备，居民通勤距离普遍较短[50]，对交通设施的需求也相对更弱。相对地，在临空港经济技术开发区等建设相对较晚的其他地区，交通出行需求较大，交通设施成为购房选择时的因素之一，回归系数出现低—低集聚。
此外，不同于地铁站，公交站距离因子的回归系数在光谷新城等区域呈现为较大的正值，说明在这些地区公交站反而对房价产生了抑制作用，由于该地区居民平均收入水平较高，私家车保有量大，道路交通拥堵情况较为多见。由于公交停站对交通流的干扰，公交车站的设立会降低道路通行能力、增加拥堵概率[51]。在这种情况下，公交站距离因子实际作为交通拥挤情况的代理变量参与回归，表现出对房价的负面影响。

5 结论与讨论

5.1 结论

为提升城市住房价格空间非平稳关系的建模精度，精确刻画城市房价影响因子的驱动机制，本文提出了一种基于TD-GNNWR的房价估算模型。该模型采用出行时间作为GNNWR模型的空间度量，提高了房价建模中空间邻近性表达的准确性，并利用GNNWR的空间加权神经网络实现了空间回归系数的精确求解，提升了城市房价影响因子回归分析的空间建模能力。面向武汉市的住房价格建模问题，将TD-GNNWR模型与其他回归模型进行实例验证和对比，结果表明：
（1）与OLR、GWR和GNWWR方法相比，本文提出的TD-GNNWR方法在面向城市住房的回归建模中具有明显优势，TD-GNNWR拟合的房价在武汉市研究区域内（特别是新洲区等样本点稀疏区域）具有更高的精度，其空间形态分布也更接近真实分布情况。
（2）TD-GNNWR可以较好地描述武汉市房价及其影响因子的空间异质性，所得房价及相关因子的空间分布与现有其他研究[16,43,45⇓⇓⇓⇓⇓ -51]结果相符，具有较好的可解释性和科学意义。
（3）武汉市住房价格受建筑特征、邻里特征和交通设施可达性等多方面因子的综合影响，其中绿化率、物业费、小学、大学、公交因子对武汉市房价有较大影响；同时，相关因子在武汉市内不同区域对房价具有不同的影响方向与强度，具有明显的空间分异性。

5.2 讨论

本文提出的TD-GNNWR模型通过引入出行时间作为空间度量，能够更准确地刻画城市房价的空间非平稳性、深入揭示房价影响因子的作用机制和空间差异，从而较好地满足政府、城市规划部门、房地产开发商和市场投资者对政策制定、宏观调控、城市规划和投资决策等任务的需求。同时，本文还可为类似城市房价建模问题提供启示，拓展房地产研究的方法和视角。
然而，本文仍存在一定不足：① 房屋建成时间对二手房价格具有重要影响，受限于数据可获取性，本文未能建立包含房屋建成时间的数据集；② 由于中小学的教学质量较难量化，仅使用与学校的距离作为因子的量化方式，这导致回归结果难以充分反映“学区房”概念；③ 研究样本仅来自于2019年，样本量较小，需要进一步扩展样本年限，并考虑在模型中引入时间距离进行时空混合建模；③ 二手房价格受交易税、首付比例、贷款年限和利率等政策性因素影响，随着研究样本扩大到多年的面板数据，需要考虑各截面间的政策差异及其对房价造成的影响。
未来研究将着重解决这些不足之处，结合TD-GNNWR模型在空间邻近性度量和空间非平稳权重解算精度上的优势，形成更具普适性和科学性的房价建模方法。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
[1]
Yan Se, Zhu Guozhong. House slave effect or wealth effect: A theoretical analysis of the impact of rising house prices on national consumption. Management World, 2013, 29(3): 34-47.

[颜色, 朱国钟. “房奴效应”还是“财富效应”? 房价上涨对国民消费影响的一个理论分析. 管理世界, 2013, 29(3): 34-47.]

[2]
Du Li, Pan Chunyang, Zhang Suyu, et al. How do house prices affect consumption: Promote or suppress? Empirical evidence from 172 prefecture-level cities in China. Zhejiang Social Sciences, 2010(8): 24- 30, 126-127.

[杜莉, 潘春阳, 张苏予, 等. 房价上升促进还是抑制了居民消费: 基于我国172个地级城市面板数据的实证研究. 浙江社会科学, 2010(8): 24- 30, 126-127.]

[3]
Chen Yanbin, Qiu Zhesheng. How does housing price affect household saving rate and wealth inequality? Economic Research Journal, 2011, 46(10): 25-38.

[陈彦斌, 邱哲圣. 高房价如何影响居民储蓄率和财产不平等. 经济研究, 2011, 46(10): 25-38.]

[4]
Yuan Dong, He Qiugu, Zhao Bo. The determinants of house price: Literature review. Research on Economics and Management, 2016, 37(3): 77-85.

[袁东, 何秋谷, 赵波. 房价变动的影响因素研究: 一个文献综述. 经济与管理研究, 2016, 37(3): 77-85.]

[5]
Cai Yuanyuan, Zhu Yingming, Ai Shaowei. Impacts of regional integration on the spatial differentiation of urban housing prices: A case study of Kaifeng city, Henan province. Areal Research and Development, 2021, 40(2): 62-67.

[蔡媛媛, 朱英明, 艾少伟. 城市住宅价格空间分异的区域一体化因素分析: 以河南省开封市为例. 地域研究与开发, 2021, 40(2): 62-67.]

[6]
Tu Jin, Jiang Wanchen, Leng Zhengxing. Differentiation research on influencing factors of urban housing prices in China: Analysis based on big data of second-hand housing market in Chengdu. Price: Theory & Practice, 2021(10): 75-78.

[涂锦, 蒋宛晨, 冷正兴. 我国城市房价影响因素的差异化研究: 基于成都市二手房市场大数据的分析. 价格理论与实践, 2021(10): 75-78.]

[7]
Zhao Yang, Wang Xiaodan. A summary of the research on the influencing factors of housing prices in China. China Market, 2017(25): 18-19.

[赵杨, 王小丹. 中国房价影响因素的研究综述. 中国市场, 2017(25): 18-19.]

[8]
Rosen S. Hedonic prices and implicit markets: Product differentiation in pure competition. Journal of Political Economy, 1974, 82(1): 34-55.

[9]
Lancaster K J. A new approach to consumer theory. Journal of Political Economy, 1966, 74(2): 132-157.

[10]
Hao Qianjin. Research on the hedonic price method and the determination mechanism of residential housing prices in Shanghai[D]. Shanghai: Fudan University, 2007.

[郝前进. 特征价格法与上海住宅价格的决定机制研究[D]. 上海: 复旦大学, 2007.]

[11]
Song Weixuan, Mao Ning, Chen Peiyang, et al. Coupling mechanism and spatial-temporal pattern of residential differentiation from the perspective of housing prices: A case study of Nanjing. Acta Geographica Sinica, 2017, 72(4): 589-602.

DOI

[宋伟轩, 毛宁, 陈培阳, 等. 基于住宅价格视角的居住分异耦合机制与时空特征: 以南京为例. 地理学报, 2017, 72(4): 589-602.]

DOI

[12]
Brunsdon C, Fotheringham A S, Charlton M E. Geographically weighted regression: A method for exploring spatial nonstationarity. Geographical Analysis, 1996, 28(4): 281-298.

[13]
Zhang Jinting, Zhao Rui. Study on the influence factors of housing price in the urban area of Bohai Ring Megalopolis based on geographically weighted regression. Territory & Natural Resources Study, 2019(1): 87-93.

[张金亭, 赵瑞. 基于地理加权回归的环渤海城市群房价影响因子研究. 国土与自然资源研究, 2019(1): 87-93.]

[14]
Zhou Ran. Analysis of the spatial-temporal differentiation pattern of housing price in Northeast China and its influencing factors[D]. Changchun: Northeast Normal University, 2021.

[周冉. 东北地区房价时空分异格局及影响因素分析[D]. 长春: 东北师范大学, 2021.]

[15]
Xu Danmeng, Li Xin, Zhang Suwen. Spatial differentiation patterns and influencing factors analysis of housing prices in Shenyang. Human Geography, 2021, 36(6): 125-134.

[徐丹萌, 李欣, 张苏文. 沈阳市住房价格空间分异格局及其影响因素研究. 人文地理, 2021, 36(6): 125-134.]

[16]
Wang Xiulan, Fu Jiyuan, Lyu Tianyu. Study on the spatial heterogeneity of influencing factors of housing price from the perspective of city center functional differentiation: A case study on Wuhan city. Prices Monthly, 2022(2): 1-9.

[王秀兰, 付纪元, 吕天宇. 城市中心职能分异视角下住宅价格影响因素的空间异质性研究: 以武汉市为例. 价格月刊, 2022(2): 1-9.]

[17]
Osland L. An application of spatial econometrics in relation to hedonic house price modeling. Journal of Real Estate Research, 2010, 32(3): 289-320.

[18]
Liu N H, Strobl J. Impact of neighborhood features on housing resale prices in Zhuhai (China) based on an (M)GWR model. Big Earth Data, 2023, 7(1): 146-169.

[19]
Wang Z M, Wang Y C, Wu S S, et al. House price valuation model based on geographically neural network weighted regression: The case study of Shenzhen, China. ISPRS International Journal of Geo-Information, 2022, 11(8): 450. DOI: 10.3390/ijgi11080450.

[20]
Limsombunc V, Gan C, Lee M. House price prediction: Hedonic price model vs. artificial neural network. American Journal of Applied Sciences, 2004, 1(3): 193-201.

[21]
Selim H. Determinants of house prices in Turkey: Hedonic regression versus artificial neural network. Expert Systems with Applications, 2009, 36(2): 2843-2852.

[22]
McCluskey W, Davis P, Haran M, et al. The potential of artificial neural networks in mass appraisal: The case revisited. Journal of Financial Management of Property and Construction, 2012, 17(3): 274-292.

[23]
Du Z H, Wang Z Y, Wu S S, et al. Geographically neural network weighted regression for the accurate estimation of spatial non-stationarity. International Journal of Geographical Information Science, 2020, 34(7): 1353-1377.

[24]
Du Z H, Qi J, Wu S S, et al. A spatially weighted neural network based water quality assessment method for large-scale coastal areas. Environmental Science and Technology, 2021, 55(4): 2553-2563.

DOI PMID

[25]
Chen Y J, Wu S S, Wang Y Y, et al. Satellite-based mapping of high-resolution ground-level PM2.5 with VIIRS IP AOD in China through spatially neural network weighted regression. Remote Sensing, 2021, 13(10): 1979. DOI: 10.3390/rs13101979.

[26]
Wu Sensen. The theory and method of geographically and temporally neural network weighted regression[D]. Hangzhou: Zhejiang University, 2018.

[吴森森. 地理时空神经网络加权回归理论与方法研究[D]. 杭州: 浙江大学, 2018.]

[27]
Comber A, Chi K, Huy M Q, et al. Distance metric choice can both reduce and induce collinearity in geographically weighted regression. Environment and Planning B: Urban Analytics and City Science, 2020, 47(3): 489-507.

[28]
Lu B B, Charlton M, Brunsdon C, et al. The Minkowski approach for choosing the distance metric in geographically weighted regression. International Journal of Geographical Information Science, 2016, 30(2): 351-368.

[29]
Lu B B, Charlton M, Harris P. Geographically weighted regression using a non-euclidean distance metric with simulation data//2012 First International Conference on Agro- Geoinformatics. Shanghai: Agro-Geoinformatics, 2012: 1-4.

[30]
Lu B B, Charlton M, Fotheringhama A S. Geographically weighted regression using a non-euclidean distance metric with a study on London house price data. Procedia Environmental Sciences, 2011, 7: 92-97.

[31]
Wang Zhongyi. The method of global spatial-temporal complex proximity neural network weighted regression[D]. Hangzhou: Zhejiang University, 2020.

[王中一. 顾及全域时空复杂邻近性的神经网络加权回归方法[D]. 杭州: 浙江大学, 2020.]

[32]
Ji Xiaofeng. Geographically convolutional neural network weighted regression and its empirical analysis in PM2.5 modeling[D]. Hangzhou: Zhejiang University, 2019.

[嵇晓峰. 地理卷积神经网络加权回归方法及其PM2.5建模实证研究[D]. 杭州: 浙江大学, 2019.]

[33]
Fan Qiao, Guo Aijun. New advances in geographically weighted regression modeling methods and research. The Journal of Quantitative Economics, 2021, 12(2): 134-150.

[范巧, 郭爱君. 地理加权回归模型方法与研究新进展. 数量经济研究, 2021, 12(2): 134-150.]

[34]
Lu Binbin, Ge Yong, Qin Kun, et al. A review on geographically weighted regression. Geomatics and Information Science of Wuhan University, 2020, 45(9): 1356-1366.

[卢宾宾, 葛咏, 秦昆, 等. 地理加权回归分析技术综述. 武汉大学学报(信息科学版), 2020, 45(9): 1356-1366.]

[35]
Wang Menghan. A study on the influencing factors of housing price in Beijing based on GTWR model[D]. Taian: Shandong Agricultural University, 2018.

[王梦晗. 基于时空地理加权回归模型的北京市房价影响因素研究[D]. 泰安: 山东农业大学, 2018.]

[36]
Lu Binbin, Yang Huan, Sun Huabo, et al. Algorithm of approximating road network distance via the Minkowski distance. Geomatics and Information Science of Wuhan University, 2017, 42(10): 1373-1380.

[卢宾宾, 杨欢, 孙华波, 等. 利用Minkowski距离逼近道路网络距离算法研究. 武汉大学学报(信息科学版), 2017, 42(10): 1373-1380.]

[37]
Liu J P, Yang Y, Xu S H, et al. A geographically temporal weighted regression approach with travel distance for house price estimation. Entropy, 2016, 18(8): 303. DOI: 10.3390/e18080303.

[38]
Fotheringham A S, Brunsdon C, Charlton M. Geographically Weighted Regression:The Analysis of Spatially Varying Relationships. New York: John Wiley & Sons, 2003: 27-64.

[39]
Fotheringham A S, Yang W B, Kang W. Multiscale geographically weighted regression (MGWR). Annals of the American Association of Geographers, 2017, 107(6): 1247-1265.

[40]
Lu B B, Brunsdon C, Charlton M, et al. Geographically weighted regression with parameter-specific distance metrics. International Journal of Geographical Information Science, 2017, 31(5): 982-998.

[41]
Qin Wenzhong. The basic theoretics and application research on geographically weighted regression[D]. Shanghai: Tongji University, 2007.

[覃文忠. 地理加权回归基本理论与应用研究[D]. 上海: 同济大学, 2007.]

[42]
Kang Y H, Zhang F, Gao S, et al. Human settlement value assessment from a place perspective: Considering human dynamics and perceptions in house price modeling. Cities, 2021, 118(2): 103333. DOI: 10.1016/j.cities.2021.103333.

[43]
Gao Hua. Research on spatial differentiation and influencing factors of second-hand house prices in the Third Ring Road of Wuhan[D]. Wuhan: Wuhan University, 2020.

[高华. 武汉市三环线内二手房价空间分异及影响因素研究[D]. 武汉: 武汉大学, 2020.]

[44]
Moran P A P. The interpretation of statistical maps. Journal of the Royal Statistical Society Series B: Statistical Methodology, 1948, 10(2): 243-251.

[45]
Ge Tianren, Li Qiang. The four models of community governance in urban China. Journal of Northwest Normal University (Social Sciences), 2016, 53(6): 5-13.

[葛天任, 李强. 我国城市社区治理创新的四种模式. 西北师大学报(社会科学版), 2016, 53(6): 5-13.]

[46]
Liu Yuhui, Zhang Chi, Hou Yunpeng. Spatial distribution characteristics of the green space in the main urban area of Wuhan based on large data. Huazhong Architecture, 2018, 36(11): 77-81.

[刘育晖, 章迟, 侯云鹏. 基于大数据的武汉主城区公园绿地使用空间分布特征研究. 华中建筑, 2018, 36(11): 77-81.]

[47]
Zhang Yuyang, Sun Yating, Yao Chonghuai. The application of spatial syntax in the accessibility study of urban parks: A case study of Wuhan. Chinese Landscape Architecture, 2019, 35(11): 92-96.

[张玉洋, 孙雅婷, 姚崇怀. 空间句法在城市公园可达性研究中的应用: 以武汉三环线内城市公园为例. 中国园林, 2019, 35(11): 92-96.]

[48]
He Qian. Research on spatial allocation characteristics and improvement strategy of basic education facilities: Taking the main city of Wuhan as an example[D]. Wuhan: Huazhong University of Science & Technology, 2019.

[何倩. 基础教育设施空间配置特征及优化策略研究[D]. 武汉: 华中科技大学, 2019.]

[49]
Wen H Z, Xiao Y, Hui E C M, et al. Education quality, accessibility, and housing price: Does spatial heterogeneity exist in education capitalization? Habitat International, 2018, 78: 68-82.

[50]
Liu Yaolin, Chen Long, An Zihao, et al. Research on job-housing and commuting in Wuhan based on bus smart card data. Economic Geography, 2019, 39(2): 93-102.

[刘耀林, 陈龙, 安子豪, 等. 基于公交刷卡数据的武汉市职住通勤特征研究. 经济地理, 2019, 39(2): 93-102.]

[51]
Jia Bin, Li Xingang, Jiang Rui, et al. The influence of bus stop on the dynamics of traffic flow. Acta Physica Sinica, 2009, 58(10): 6845-6851.

[贾斌, 李新刚, 姜锐, 等. 公交车站对交通流影响模拟分析. 物理学报, 2009, 58(10): 6845-6851.]

Options
文章导航

/

〈 〉