EN中文

地理学报 >

2023 , Vol. 78 >Issue 6: 1484 - 1497

DOI: https://doi.org/10.11821/dlxb202306010

人口与城市研究

面向15 min生活圈的城市服务设施规划模型与实验

  • 翟石艳 , 1 ,
  • 孔云峰 , 1 ,
  • 宋根鑫 2 ,
  • 罗静静 2
展开
  • 1.河南大学黄河中下游数字地理技术教育部重点实验室，开封 475004
  • 2.河南大学地理与环境学院，开封 475004
孔云峰(1967-), 男, 教授, 博士生导师, 主要从事空间分析、空间优化等研究。E-mail:

翟石艳(1983-), 女, 副教授, 博士生导师, 主要从事空间分析、空间优化和空间行为决策等研究。E-mail:

收稿日期: 2022-01-17

  修回日期: 2022-12-29

  网络出版日期: 2023-06-21

基金资助

国家自然科学基金项目(41871307)

河南省高等学校重点科研项目(21A170007)

2022年度河南省政府决策研究招标课题(2022JC015)

收起

A new facility location problem for urban public facility planning toward 15-minute life circle: Model and experiment

  • ZHAI Shiyan , 1 ,
  • KONG Yunfeng , 1 ,
  • SONG Genxin 2 ,
  • LUO Jingjing 2
Expand
  • 1. Key Laboratory of Geospatial Technology for the Middle and Lower Yellow River Regions, Ministry of Education, Henan University, Kaifeng 475004, Henan, China
  • 2. College of Geography and Environmental Science, Henan University, Kaifeng 475004, Henan, China

Received date: 2022-01-17

  Revised date: 2022-12-29

  Online published: 2023-06-21

Supported by

National Natural Science Foundation of China(41871307)

Key Scientific Research Project of Henan Institution of Higher Education(21A170007)

2022 Henan Provincial Government Decision-making Research Bidding Project(2022JC015)

Fold

摘要

生活圈规划是城市公共资源均等化配置和可持续发展的重要抓手。特定城市15 min生活圈服务设施规划实践中，针对某一类公共服务，如何确定其设施数量、空间位置和服务公平性，具有诸多挑战。为回答这一问题，本文首次改进经典的设施区位问题（CFLP）为服务半径和覆盖率双重约束下的部分覆盖问题（μ CFLP），使其适用于生活圈服务设施布局规划。构造μ CFLP线性规划模型，设计数学启发求解算法。按照中国城市规模划分标准，选择6个典型城市案例区域，以社区卫生服务中心为例，进行服务设施布局规划实验。结果表明：改进模型适用于城市生活圈服务设施布局规划，能够平衡服务供给成本、可及性和公平性；在人口密度较低的城市，模型对服务半径和覆盖率参数设置敏感，服务质量与效率难以兼顾，而在人口密度高的大都市，相对容易满足15 min生活圈建设标准。本文模型在面向15 min生活圈的城市服务设施规划方面具有明显的优势，一是无须事先确定设施数量，二是能够按覆盖半径与覆盖率探索最优设施布局。

关键词： 公共服务设施规划; 15 min生活圈; 设施区位问题; 案例实验

本文引用格式

翟石艳 , 孔云峰 , 宋根鑫 , 罗静静 . 面向15 min生活圈的城市服务设施规划模型与实验[J]. 地理学报, 2023 , 78(6) : 1484 -1497 . DOI: 10.11821/dlxb202306010

Abstract

The planning and construction of urban 15-minute life circle is a key tool for equally allocating urban public resources and promoting sustainable development. However, it is challenging to design the public service systems toward urban living circle: how many service facilities are required, where to locate the facilities, and how to promote service equality for urban residents. A new facility location problem was proposed for public facility planning toward urban living circle. The new problem, μ CFLP, is a variant of classical capacitated facility location problem (CFLP) with constraints of maximum service radius and partial demand covering. A mixed integer linear programming model was formulated for the μCFLP and a matheustic algorithm was designed for solving this model. The model and the solution method were tested on 6 study areas. According to the Chinese city scale classification standard, 6 typical urban regions in China were selected. Then, the community health service center was taken as a service example to conduct the service facility layout planning experiment. The results show that: (1) the new model can balance the service quality, efficiency and fairness, and thus can be applied to the layout planning of public service facilities toward urban living circle. (2) In cities with low population density, the model is sensitive to the two planning parameters: service radius and coverage; and thus it is necessary to balance service quality and efficiency. While in the metropolis with high population density, it is relatively easy to meet the construction standard of 15-minute life circle. The experimental results show that the model proposed in this study has obvious advantages for the planning of urban service facilities toward the 15-minute life circle goal. First, the number of facilities need not be determined in advance. Second, the optimal layout of facilities can be explored according to the combination of coverage radius and coverage parameters.

Key words： public service facility planning; 15-minute life circle; facility location problem; case study

1 引言

快速城镇化和转型发展背景下，中国城市公共服务资源不足且空间布局不均衡现状与人们追求高品质美好生活的向往间的矛盾日益加剧，致使城市规划建设的思路也发生了人本转向[1-2]。2016年2月《中央国务院关于进一步加强城市规划建设管理工作的若干意见》首次提出要“打造方便快捷生活圈”。2016年8月上海率先提出了《上海市15分钟社区生活圈规划导则》。2018年住建部将“15 min生活圈居住区”纳入新版城市居住区规划设计标准[3]。随后，北京、广州、武汉、杭州、长沙等城市相继开展了城市生活圈规划实践[4-5]。以满足城市居民日常需求为重点的“生活圈规划”得到政府和学术界的广泛认可，成为城市公共资源均等化配置和可持续发展的重要抓手。公共服务设施布局规划是构建15 min生活圈的重点任务之一。
然而，生活圈服务设施空间配置理论和实践方法尚不成熟，满足15 min生活圈的服务设施规划问题仍面临诸多挑战[6⇓⇓-9]。① 针对某一区域，给定生活圈服务半径和服务覆盖率，需要配置多少设施；② 规划的设施位置如何确定，建设成本如何；③ 服务设施的可达性和公平性是否合理。因此，如何构建一套科学有效的面向生活圈的公共服务设施布局优化模型或问题求解框架，对于15 min生活圈规划理论方案制定和实现后疫情时代城市可持续发展具有重要的现实意义。
鉴于现有区位问题难以适应“15 min生活圈”服务设施规划，本文改进经典的容量约束设施区位问题（Capacitated facility location problem, CFLP）为服务半径和服务覆盖率μ约束下的区位问题，平衡设施运营效率、服务质量和空间公平性，优化设施数量和使用服务的距离成本。CFLP属于数学难题问题，计算复杂度高，求解难度极高。服务半径和服务覆盖率约束使新模型比经典模型更难以求解。本文设计专门的数学启发算法求解新提出的区位问题。考虑城市等级和人口规模因素，依据中国城市规模划分标准[10]，选择6个典型城市，以城市社区卫生服务中心布局规划为例，验证μ CFLP模型的有效性。案例实验表明本文模型克服了经典模型的局限，适用于城市生活圈服务设施规划。

2 文献回顾

“生活圈”指的是城市居民满足生存、发展与交往需要，开展各类生产和生活活动所涉及的空间范围[11-12]。建设的核心内容为在居民步行范围内，完善基础设施和公共空间的配置水平[3,13 -14]。以居住地为中心，采用步行方式完成购物、休闲、通学和社会交往等日常生活活动[15]。近年来，国内学者围绕生活圈界定、空间范围识别划定和服务设施配置方法进行了广泛讨论和实践[2,9,11,16 -17]。部分学者[4,8,16⇓⇓⇓ -20]基于生活圈理论，从供需匹配视角探讨公共服务设施布局模式与配置策略。例如，柴彦威等[16]采用居民日常活动的GPS数据与活动日志数据，顾及居民日常活动特征及对公共服务设施的需求，构建“社区—行为谱系”与“人群—行为谱系”，提出社区生活圈公共服务设施优化方案。周岱霖等[17]探讨设施空间供给与居民需求的分异问题。周弦[18]采用步行指数方法，分析单元规划公共服务设施布局的可步行和合理性。然而，现有研究仅关注于单个生活圈内部供给和需求匹配程度，对城市生活圈整体供需平衡考虑不足。
公共服务设施规划需考虑社区服务半径要求和人口变化趋势。例如，常飞等[21]从生活圈的视角，探讨了城市公共服务设施与人口的匹配程度。部分学者[18,22⇓ -24]考虑社区不同群体步行活动与行为需求的特殊性，结合服务设施可达性和可步行性评价结果，对设施布局提出优化策略。例如，Weng等[22]以上海市为例，基于道路舒适度概念评估社区不同群体（儿童、成人和老年人）的步行需求和服务设施可达性，进而提出15 min城市建设策略。但现有研究存在实时个体数据获取困难，数据精度不高，研究方法和结果难以推广等不足。另外，个别研究[9]考虑了社区服务半径的差异化需求，但社区生活圈的服务半径和公共服务设施如何配置仍未给出明确方案。规划实践时，如果《城市居住区规划设计标准》所给出的生活圈建设指南与地方的实际情况不相匹配，高于或低于国家标准该怎么办，已有研究也未给出答案，需进一步探索。
与服务设施布局相关的区位问题研究已有60余年历史。经典的区位问题包括集覆盖区位问题（Set Covering Location Problem, SCLP）[25]、P中值问题（P-median Problems, PMP）[26]、P中心问题（P-center Problem, PCP）[27]、最大覆盖区位问题（Maximum Covering Location Problem, MCLP）[28]、设施区位问题（Uncapacitated Facility Location Problem, UFLP）[29]以及这些问题的扩展[30⇓⇓⇓⇓-35]。这些区位模型在公共服务设施规划中得到广泛应用，如交通、物流、通讯、应急、教育等服务设施规划[36⇓⇓⇓⇓⇓-42]。PMP、PCP、SCLP、MCLP、UFLP等经典的区位问题，均是从候选区位中选择部分区位，用于建设服务设施，并确定设施为哪些需求区位提出服务。PMP、PCP和MCLP需要事先确定设施数量，PMP优化总旅行成本，PCP最小化最大旅行距离，而MCLP最大限度地满足需求；SCLP和UFLP不需要事先确定设施数量，前者尽可能使用最少的设施或者总成本最低的设施，后者兼顾设施成本和总旅行成本。因区位问题计算复杂度高，早期的模型往往不考虑设施服务能力限制。随计算机计算能力的提升，经典区位问题逐渐加入设施容量限制，如容量约束PMP（CPMP）[30]、容量约束PCP（CPCP）[31-32]、容量约束SCLP[33]、容量约束MCLP和容量约束设施区位问题（CFLP）[34]。常见区位问题的约束条件和目标函数类型汇总如表1所示。
表1 常见区位问题的约束条件和目标函数类型

Tab. 1 Constraints and objective function types of classical location problems

问题模型 设施数量
约束		 设施容量
约束		 服务半径
约束		 满足所有
需求		 设施成本
目标		 距离成本
目标		 最大距离
目标		 最大覆盖
目标
PMP √ × × √ × √ × ×
CPMP √ √ × √ × √ × ×
PCP √ × × √ × × √ ×
CPCP √ √ × √ × × √ ×
UFLP × × × √ √ √ × ×
CFLP × √ × √ √ √ × ×
SCLP × × √ √ √ × × ×
容量约束SCLP × √ √ √ √ × × ×
MCLP √ × √ × × × × √
容量约束MCLP √ √ √ × × × × √

注：“√”表示满足约束条件或目标函数，“×”表示不满足约束条件或目标函数。

为满足公共服务设施空间可达性和空间公平性需求，通常将最大服务半径作为服务设施规划的一个重要指标。然而考虑服务半径约束的SCLP和MCLP仍有局限性。若设施服务半径较小，SCLP模型结果中，所需设施数量往往很多，设施建设成本高且利用率低，影响服务供给效率。MCLP模型事先指定设施数量，最大限度地满足服务需求，若服务半径较小，将有较大数量的需求得不到满足。有学者将服务半径引入PMP[43]，提升服务质量，但往往会损失服务供给效率。另一方面，有学者提出部分覆盖区位问题，尝试通过适当降低服务质量提升服务供给效率。例如部分覆盖PMP[44]、部分覆盖UFLP[45-46]、部分覆盖SCLP[44,47]。这些部分覆盖模型，在应用中具有灵活性，能较为有效地提升服务供给效率，但忽略了部分区位的公共服务。同时，这些部分覆盖模型未考虑设施服务能力，实践中很多公共服务必须考虑设施的服务能力。
区位问题求解算法极其多样。① 不同的区位问题类型，因其约束条件和目标函数的差异，求解算法往往有很大的差异；② 即使针对同一问题，因区位问题属于数学难题，学者一直在寻求新的方法进行求解；③ 随区位问题、优化算法理论研究的不断深入，学者不断提出新的求解算法。区位问题算法大致划分为：精确算法、基于拉格朗日松弛的启发算法、基于局部搜索的启发式算法、基于群智能的启发算法、基于生物演化的启发算法等[48-49]。
综上，随着中国城市15 min生活圈规划理念的逐步普及，越来越多的学者尝试通过城市圈层结构划分、居民出行大数据分析划定城市生活圈，进而通过供需匹配进行各类设施布局规划。在规划实践中，规划专家在服务设施规划方面总结了一些规律，也遇到了诸多挑战。另一方面，区位问题已广泛应用于公共服务设施规划，但对于生活圈设施规划仍存在局限性。例如，经典问题及其扩展难以兼顾设施运行效率、服务质量和空间可达性；部分覆盖区位问题能够兼顾设施效率、服务质量和空间可达性，但现有模型仅针对不考虑设施服务能力的简单场景，仍难以适用于幼儿园、中小学校、卫生服务中心、日间照料中心等服务设施规划。因此，有必要构建新的区位问题模型，适用于生活圈的公共服务设施布局。

3 问题定义与算法设计

3.1 问题定义

本文将城市生活圈服务设施规划问题抽象如下：给定城市基本空间单元、单元内需求数量、候选设施空间位置和设施的最大服务容量，选择一定数量的区位建设服务设施，满足所有单元的服务需求及特定服务半径和需求覆盖率要求，目标是所需服务设施的数目最少，使用服务的旅行成本最低。
令集合 I = 1 ,   2 , ⋯ ,   n表示n个候选服务设施区位，设施 i i ∈ I有最大服务容量Si和设施成本fi。令集合 J = 1 ,   2 , ⋯ ,   m表示m个需求点，需求点 j j ∈ J的服务需求量为dj。空间单元i与单元j之间的距离成本为cij。定义布尔型决策变量xij为是否指派设施i服务到需求空间j，布尔型决策变量yi表示是否在区位i上建设施，经典的单源CFLP模型如下：
M i n i m i z e :   ∑ i ∈ I f i y i + ∑ i ∈ I ∑ j ∈ J d j c i j x i j
S u b j e c t   t o :   ∑ i ∈ I x i j = 1 , ∀ j ∈ J                                
    ∑ j ∈ J d j x i j ≤ s i y i ,   ∀ i ∈ I
                            x i j ,   y i ∈ 0 ,   1 ,   ∀ i ∈ I ,   j ∈ J
目标函数（1）最小化设施固定成本和使用服务的旅行成本；约束（2）保证每一个空间单元需求必须获得公共服务；约束（3）保证每一个设施服务分配的服务量不超过其供给量；条件（4）定义决策变量xij和yi。
生活圈服务规划对于不同类型设施的服务半径有特定的要求，然而经典的CFLP模型未考虑设施服务半径，往往会造成部分区位距离服务设施过远，也缺乏空间公平性方面的考虑。为克服这一局限，可在模型中引入覆盖半径进行改进。令服务半径为ϕ，在约束（2）中加入服务半径限制，约束条件为：。
∑ i ∈ I , d i j ≤ ∅ x i j = 1 ,   ∀ j ∈ J
模型改进后，所有区位能够满足服务半径要求。然而，约束条件（5）往往会导致所需设施数量大幅增加。例如，某城市人口约为71万人，面积132 km2，不考虑覆盖半径，8个社区卫生中心可服务所有人口，使用服务的平均旅行距离为1.47 km；但给定服务半径为2.0 km，所需建设的社区卫生中心数量则增至24个。
为平衡服务成本、质量和空间公平性，引入最低覆盖率μ对服务半径ϕ进行补充。在经典模型中增加新的约束条件（6），即设施在服务半径内覆盖需求总量满足最低覆盖率指标。
∑ i ∈ I ∑ j ∈ J , d i j ≤ ∅ d j × x i j ≥ μ × ∑ j ∈ J d j
经典的CFLP模型优化设施建设成本和距离成本。考虑到设施建设成本在规划阶段难以精确地估算，可将建设成本设置为一个较大的固定数值M，从而将目标函数（1）修改为（7）。因参数M值较大，目标函数优先考虑设施数量，再降低使用服务的距离成本。
M i n i m i z e :               M ∑ i ∈ I y i + ∑ i ∈ I ∑ j ∈ J d j c i j x i j
综上，经典的CFLP数学模型包括目标函数（1）和约束条件（2）~（4）；加入服务半径约束的CFLP模型包括目标函数（1）和约束条件（3）~（5）；而引入最低覆盖率的μ CFLP模型包括目标函数（7）和约束条件（2）~（4）和（6）。经典的CFLP是μ CFLP的一个特例，即服务半径无限大且覆盖率为100%；服务半径约束的CFLP也是μ CFLP的一个特例，即覆盖率为100%。μ CFLP模型综合考虑了服务半径和覆盖率，与城市生活圈规划导则的要求相吻合，在理论上适用于生活圈服务设施规划。

3.2 算法设计

服务半径和覆盖率约束使城市生活圈服务设施规划问题求解具有挑战性。经典的设施区位问题是计算复杂度极高的数学难题，增加服务半径和覆盖率约束条件进一步增加了问题求解难度。本文借鉴单源CFLP数学启发算法[50]进行求解。算法原理为：① 使用构造启发式算法获得问题初始解；② 从当前解中随机选择一个超大邻域，获取邻域内需求点、当前设施和候选设施集合；③ 构造邻域内子问题模型，求解模型获得局部解，并使用局部解更新当前全局解；④ 重复执行步骤②和③，直到若干次尝试不能更新当前解。步骤②构造一个大邻域，步骤③用于发现邻域内的最优解。基于这一思路，设计数学启发算法示意如下：
参数：连续未更新最好解循环数(mloops)
① s = Generate Initial Solution( );
② notImpr = 0;
③ While NotImpr<mloops:
④ I*, J* = Select A Neighborhood(s);
⑤ s* = Solve Sub Problem(I*, J*)
⑥ s' = Update Solution(s, s*);
⑦ If f(s')<f(s): s = s', notImpr = 0;
⑧ Else: notImpr+= 1;
⑨ Output(s).
算法中，步骤①使用经典的DROP方法[51]生成初始解。首先，在所有候选区位开设服务设施，并为所有需求区位指派服务设施；其次，以贪心的方式逐个移除设施，保证约束条件②、③和⑥得到满足，且节约成本为最高。当剩余设施不能被移除时，将当前设施和需求指派作为初始解。
步骤④从当前解中随机选择一个超大邻域，包括设施子集I*和需求子集J*。选择步骤为：首先，随机选择一个需求点，以该点为中心，从当前解设施区位集合中自近而远地选择Q个设施；其次，指派给Q个设施的需求点构成需求点子集J*；再次，子集J*中每个需求点最近的候选设施区位以及已选择的Q个设施区位构成子集I*。邻域选择是算法的一个关键点，邻域规模大小影响算法性能：若邻域太小（Q值较小），当前设施区位往往难以更新；若邻域过大（Q值较大），模型计算效率低。
步骤⑤使用候选设施区位子集I*和需求子集J*构造子问题模型，并用MIP优化器求解。
步骤⑥使用局部解s*更新当前全局解，获得新解s´。
步骤⑦尝试更新当前解。若新解s´优于当前解s，更新当前解；否则，维持当前解不变。
迭代执行步骤④~⑧，当连续若干次循环未能更新当前解，算法终止。作者使用Python语言实现了以上算法。算法代码、安装及使用说明见 https://github.com/yfkong/15mcity_cflp。

4 案例实验

4.1 案例数据

参考中国城市规模划分标准[30]和人口密度，本文选择6个典型城市，探索15 min社区生活圈服务设施规划。典型城市包括上海（SH）、深圳（SZ）、郑州（ZZ）、洛阳（LY）、平顶山（PD）和开封（KF），涵盖超大城市、大城市和中等城市。
本文将每个城市划分为若干基本空间单元，每个单元有一定数量的服务需求，以此为基础进行生活圈服务设施规划。案例数据准备过程为：① 下载 WorldPop2020人口密度数据（www.worldpop.org），使用各城市行政区边界剪切出城市人口密度网格；② 删除每个城市中的农区、山区、水体和低人口密度区域；③ 将城市人口密度数据进一步划分为7.5弧秒（约200~240 m）分辨率的网格，计算每个网格的人口数量，将每个单元上的人口数量作为服务需求量。
案例区的城市类别、空间单元数、人口规模、城市面积和平均人口密度统计信息见表2。其中，2020年案例区SH包括8266个人口单元，总人口约1633.53万人，面积697.02 km2。案例区KF包括2999个人口单元，总人口约71.45万人，面积132.14 km2。案例区人口密度分布如图1所示。SH平均人口密度最高，为2.34万人/km2；SZ和ZZ人口密度整体较高，分别为1.65万人/km2和1.42万人/km2；中等城市KF、LY和PD整体人口密度较低，分别为0.54万人/km2，0.58万人/km2和0.76万人/km2。
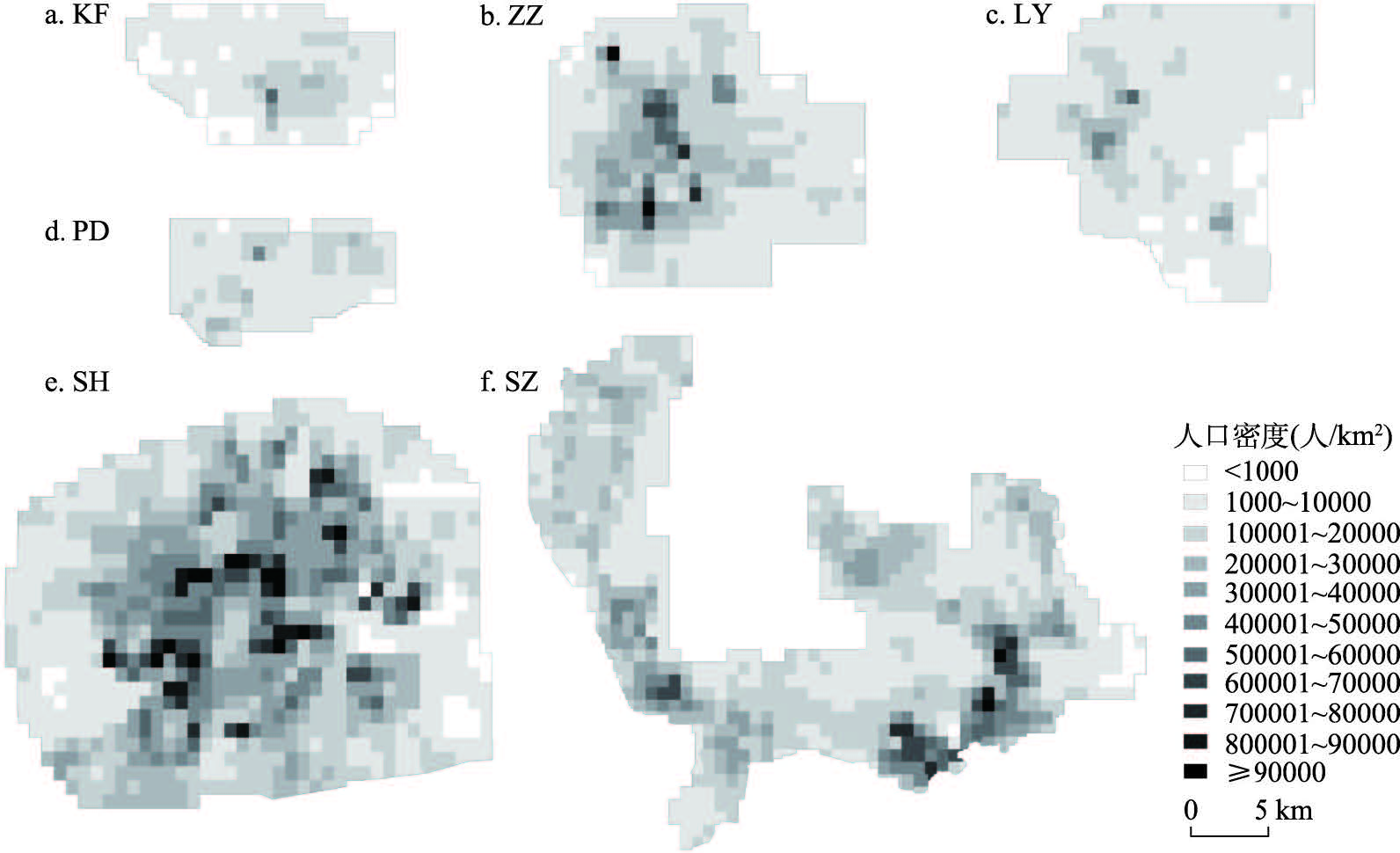
表2 2020年案例区城市类别、空间单元数、人口总数、面积和人口密度

Tab. 2 Profiles of case study areas: city category, spatial units, total population, area and population density in 2020

案例区 城市类别 空间单元数(个) 人口(万人) 面积(km2) 人口密度(万人/km2)
上海(SH) 超大城市 8266 1633.53 697.02 2.34
深圳(SZ) 超大城市 6650 1136.91 674.93 1.65
郑州(ZZ) Ⅰ型大城市 6752 422.39 297.77 1.42
洛阳(LY) Ⅱ型大城市 6040 154.43 266.54 0.58
平顶山(PD) 中等城市 2200 75.26 98.89 0.76
开封(KF) 中等城市 2999 71.45 132.14 0.54
图1 2020年案例区人口密度空间分布

Fig. 1 Population density spatial distribution in the study areas in 2020

本文以社区卫生服务中心为例，检验改进模型进行设施布局规划的可行性。假定每个单元网格均可作为候选设施区位，参考社区卫生服务中心服务能力标准（2018年版）[52]，其服务容量按其周边人口密度高低分别设置为9万/km2、7万/km2和5万/km2。针对每一个案例区，探索不同服务半径和覆盖率参数组合，所需某一类服务设施数量、空间位置及所有区位使用服务的平均距离。

4.2 实验结果及分析

本文算法使用Python程序设计，调用CPLEX优化器求解子问题模型。实验计算环境为：HP桌面计算机，配置Intel Core I7-6700 CPU 3.40 GHz、8 GB内存和Windows 10操作系统。安装软件包括Python 2.7、ArcGIS 10.0和IBM CPLEX 12.6优化器。在 ArcGIS中准备案例数据，包括城市基本空间单元及其属性di和si、单元间距离成本cij采用两个单元中心点的直线距离。
具体实验过程为：① 每个案例区采用3组参数：∅ = 1.0 km和μ = 80%；∅ = 1.5 km和μ = 80%；∅ = 1.0 km和μ = 70%；② 考虑到本文算法是随机算法，针对每个案例城市每组参数约束下的设施规划，算法运行5次，获得5个规划方案。规划方案统计见表3，其中设施数量、平均距离、计算时间均为5次计算结果的平均值，设施数量表示规划方案所需设施数量，平均距离为所有区位使用服务的加权平均距离。根据规划方案中供需指派关系，统计不同服务半径所覆盖的需求数量。
表3 不同规划参数(服务半径和覆盖率)约束下服务设施规划结果统计

Tab. 3 Statistics of the planning solutions from six study areas with different planning parameters (service radius and coverage)

城市 规划参数 设施数量
(个)		 平均距离
(km)		 计算时间
(s)		 不同服务半径的人口覆盖率(%)
< 1.0 km < 1.5 km < 2.0 km
KF ∅= 1.0 km, μ = 80% 22.0 0.781 622.42 80.2 92.3 96.6
KF ∅= 1.5 km, μ = 80% 10.2 1.121 1020.90 51.3 80.5 89.7
KF ∅= 1.0 km, μ = 70% 14.8 0.979 954.28 70.4 85.3 90.9
LY ∅= 1.0 km, μ = 80% 51.2 0.743 1413.84 80.1 94.1 98.4
LY ∅= 1.5 km, μ = 80% 26.0 1.056 1858.45 52.7 80.6 93.1
LY ∅= 1.0 km, μ = 70% 37.0 0.870 1753.85 70.1 88.4 95.4
PD ∅= 1.0 km, μ = 80% 22.2 0.719 488.09 80.5 97.5 99.8
PD ∅= 1.5 km, μ = 80% 10.4 1.037 858.92 50.7 81.4 96.0
PD ∅= 1.0 km, μ = 70% 16.8 0.823 653.43 70.8 92.9 98.8
ZZ ∅= 1.0 km, μ = 80% 61.8 0.753 2309.47 80.1 94.4 98.0
ZZ ∅= 1.5 km, μ = 80% 48.6 0.886 1893.68 68.7 88.2 95.0
ZZ ∅= 1.0 km, μ = 70% 49.2 0.880 2494.25 70.5 88.6 94.9
SZ ∅= 1.0 km, μ = 80% 145.0 0.760 3514.54 80.0 93.3 97.9
SZ ∅= 1.5 km, μ = 80% 132.2 0.848 2420.47 72.5 89.2 95.6
SZ ∅= 1.0 km, μ = 70% 133.2 0.841 2595.73 73.1 89.6 96.1
SH ∅= 1.0 km, μ = 80% 190.0 0.695 2948.15 83.6 94.1 97.7
SH ∅= 1.5 km, μ = 80% 190.0 0.692 2724.13 83.3 94.1 97.8
SH ∅= 1.0 km,   μ = 70% 188.8 0.705 2694.96 82.8 93.5 97.4
对于案例区KF，设施服务半径为1.0 km和覆盖率80%时，所需设施数量平均为22.0个，获取服务的平均旅行距离为0.78 km；当增加服务半径约束1.5 km，覆盖率80%保持不变时，所需设施数量降低为10.2个，但平均旅行距离增加为1.12 km；当服务半径为1.0 km，将覆盖率降为70%时，所需设施数量约为14.8个，平均旅行距离为0.98 km。可以看出，该区域规划方案受参数设置影响很大。在人口密度较低的案例区LY和PD，规划实验呈现出与案例区KF相似的特征：规划方案对参数设置极为敏感。
对人口密度较高的案例区ZZ和SZ，对规划参数设置较为敏感。如案例区ZZ，当满足服务半径为1.0 km和覆盖率80%时，所需设施数量为61.8个，获取服务的平均旅行距离为0.75 km；当放松服务半径约束为1.5 km或降低覆盖率为70%时，所需设施数量分别减少为48.6个和49.2个，获取服务的平均旅行距离分别增加为0.89 km和0.88 km。
而对于SH，当满足约束条件服务半径为1.0 km和覆盖率80%时，所需设施数量为190.0个；当满足约束条件服务半径为1.5 km和覆盖率80%时，所需设施数量仍为190.0个；当满足约束条件服务半径为1.0 km和覆盖率70%时，所需设施数量为188.8个。在该区域，给定不同的规划参数，所需服务设施数量和平均服务距离并未发生显著改变，相对容易满足15 min生活圈建设标准。
表3给出了每个案例不同服务半径下，设施所覆盖的人口数量百分比。针对1 km服务半径和80%覆盖率，所有规划方案均满足80%覆盖率要求；1.5 km的服务半径能覆盖92.3%~97.5%的人口，而2.0 km的服务半径能覆盖96.6%~99.8%的人口；少量人口获取服务的距离超过2.0 km。从表3中可以看出，本文算法能够在8~60 min内完成模型计算。对于空间单元数较少的案例区（PD和KF），约需8~17 min；而对于大规模案例（SZ和SH），计算时间约需要40~60 min。
图2为6个案例区3组规划参数约束下的设施区位和设施服务区示意图。服务设施布局具有两个明显的特征：① 设施分布密度与人口分布密度相一致，呈现城市中心密度高外围密度低的分布特征，城市中心区域需求区位与设施距离较近，而在城市外围地区，需求区位与设施距离相对较远；② 绝大多数设施的服务区空间连续，形状较为紧凑，设施通常位于服务区内人口较为集中的位置。这些特征与规划导则要求相一致，也符合规划人员的实践经验。
图2 案例区设定不同参数的规划方案

Fig. 2 The planning schemes with different parameters for six study areas

图3为案例区ZZ设施空间分布及服务覆盖范围示意图，服务设施空间布局呈现出明显的圈层结构。城市中心区域，设施分布较为密集，大多数区域均能在1.0 km距离范围内获取服务。而城市边缘地带，设施分布较为稀疏，有较多区域无法在1.0 km距离范围内获取服务。案例中，使用服务的平均距离为0.741 km，设施0.5 km服务半径内覆盖30.6%人口，1 km半径覆盖80.2%人口，2 km半径覆盖98.3%人口，约有1.7%人口距离最近设施距离大于2 km。更详细的服务半径及覆盖率统计如表4所示。
图3 案例区ZZ基层医疗服务设施规划方案

(∅=1.0 km, μ=80%)

Fig. 3 Diagram of a basic medical service facility planning scheme in ZZ

(∅=1.0 km, μ=80%)

表4 案例区ZZ基层医疗服务设施需求覆盖统计

Tab. 4 Demand coverage of the basic medical service facilities with different service radiuses in ZZ

服务半径(km) 覆盖人口(人) 总人口(人) 覆盖人口/总人口(%)
0.5 1293102 4223997 30.61
1.0 3386895 4223997 80.18
1.5 4001819 4223997 94.74
2.0 4154030 4223997 98.34
2.5 4204061 4223997 99.53
3.0 4221167 4223997 99.93
验证本文模型的优势，作者使用CFLP和CPMP模型进行设施布局规划，并与本文模型进行比较。以研究区ZZ为例（表5），① μ CFLP模型设置规划参数∅ = 1.0 km和μ =80%，需要设置61个设施，设施1.0 km半径的人口覆盖率为80.00%，居民与设施间的平均距离为0.743 km。② 使用CFLP模型，所需设施数量仅为49个，设施1.0 km半径的人口覆盖率为68.86%，居民与设施间的平均距离为0.846 km。③ 使用CPMP模型，设置设施数量为56个、57个、58个、59个、60个、61个和62个。随着设施数量增加，设施1.0 km半径人口覆盖率从75.76%增加到78.94%，平均距离从0.767 km下降到0.732 km。从表5可以看出，① CFLP、μ CFLP模型选择的设施数量分别为49个和61个，前者设施成本低，但设施1 km服务半径仅能覆盖69%的人口，后者能够满足设施1 km服务半径覆盖80%人口的需求。② 因CPMP模型需要确定设施数量，实际应用中需要设置多个设施数量进行尝试，结果发现按该模型设置56~62个设施，设施1 km服务半径能覆盖75%~79%的人口，仍不能满足设施1 km服务半径覆盖80%人口的需求。③ μ CFLP模型无需指定设施数量，按照规划指标进行布局设施，可平衡服务供给成本和服务可达性，在应用中具有优势。
表5 案例区ZZ服务设施规划:3个区位模型(μ CFLP, CFLP, CPMP)计算结果比较

Tab. 5 Comparison of the three location models (μCFLP, CFLP, CPMP) for service facility planning in ZZ

模型 设施数量
(个)		 平均距离
(km)		 计算时间
(s)		 不同服务半径的人口覆盖率(%)
<1 km < 1.5 km < 2 km
μ CFLP 61 0.743 4440.40 80.00 95.31 98.63
CFLP 49 0.846 2945.44 68.86 90.44 97.05
CPMP 56 0.767 2424.77 75.76 94.67 98.56
CPMP 57 0.763 2447.36 75.74 95.30 98.92
CPMP 58 0.757 3227.06 76.74 95.29 99.05
CPMP 59 0.753 3339.92 78.03 95.13 98.76
CPMP 60 0.745 3014.18 78.06 95.24 99.05
CPMP 61 0.740 2655.39 78.94 95.27 98.77
CPMP 62 0.732 2293.94 78.54 96.17 99.17

5 结论与讨论

5.1 结论

面向城市15 min生活圈的服务设施规划问题，本文在综合考虑服务半径和覆盖率前提下，首次改进经典的设施区位问题（CFLP）为服务半径和覆盖率双重约束下的部分覆盖问题（μ CFLP），构造μ CFLP线性规划模型，设计了单源CFLP数学启发求解算法。按照中国城市规模划分标准，选择6个典型城市案例区域，以社区卫生服务中心为例，进行服务设施布局规划实验。
案例研究表明：① 改进模型适用于城市生活圈服务设施布局规划，能够平衡服务供给成本和空间公平性，可以弥补现有区位模型的不足；② 与常用CFLP、CPMP模型相比，本文模型在面向15 min生活圈的城市服务设施规划方面具有明显的优势，一是无须事先确定设施数量，二是能够按覆盖半径与覆盖率指标寻找最优设施布局；③ μ CFLP模型计算复杂度较高，较小规模案例区求解时间约为8~17 min，大规模案例需要40~60 min；④ 在人口密度高的大都市，相对容易满足15 min生活圈建设标准，而在人口密度较低的城市，模型对服务半径和覆盖率参数设置敏感，设施布局受参数影响较大。

5.2 讨论

本文模型能够很好地满足国家《“十四五”公共服务规划》提出的要求：人群覆盖，服务达标；均等享有，便利可及；尽力而为，量力而行，适用于生活圈规划中教育、文化、养老、体育、休闲等居民日常需求的公共服务设施布局规划。应用流程大致为：① 采用居住社区或网格作为基本空间单元，通过人口数量与年龄结构预测每个单元的需求数量；② 针对不同类型的服务，参考其设施建设标准，遴选候选区位，并根据设施占地面积、建筑面积、资源配置等指标设置设施的最大服务能力；③ 结合城市人口密度、财政状况，确定设施服务半径和覆盖率等规划参数；④ 应用本文算法求解，获得设施区位和各设施服务区范围，并进行规划方案多种指标计算，用于规划决策。规划参数设置对规划结果影响显著，通常来说，人口密度较高的城市，建议使用规划导则推荐的服务半径（1.0 km），并设定较高的服务覆盖率（如80%~85%）；而在人口密度较低的城市，设定较为适中的服务覆盖率（如75%~80%）。在公共财政状况较好的城市，选择相对较好的覆盖率，反之选择相对较低的覆盖率。
本文模型在应用于城市生活圈服务设施规划时，需要详尽、可靠的数据支撑。① 城市空间单元划分要合理，不宜过大或过小；单元过大，不利于规划指标的精细计算；单元过小，数据准备困难，也影响模型计算效率。② 空间单元需求数量的预测需要充分考虑人口数量、年龄结构、区域规划、人口流动等因素。③ 步行时间估算是生活圈服务设施规划一个挑战，很多城市缺乏详细的步行道路网络数据。此外，服务半径和覆盖率约束使设施区位问题求解具有极大的挑战性，本文提出数学启发算法进行求解，计算性能仍有一定的提升空间。同时，现有的规划软件难以适应城市生活圈服务设施布局规划实践。后续的研究工作应当聚焦于算法求解质量、计算效率和应用工具研发。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
[1]
Qiu Baoxing. Challenges faced by China in its rapid urbanization process in the near future. Urban Studies, 2003, 10(6): 1-15.

[ 仇保兴. 我国城镇化高速发展期面临的若干挑战. 城市发展研究, 2003, 10(6): 1-15.]

[2]
Chai Yanwei, Zhang Xue, Sun Daosheng. A study on life circle planning based on space time behavioural analysis: A case study of Beijing. Urban Planning Forum, 2015(3): 61-69.

[ 柴彦威, 张雪, 孙道胜. 基于时空间行为的城市生活圈规划研究: 以北京市为例. 城市规划学刊, 2015(3): 61-69.]

[3]
Ministry of Housing and Urban-Rural Development of the People's Republic of China. Urban Residential Area Planning and Design Standards(GB50180-2018). 2018.

[ 中华人民共和国住房和城乡建设部. 城市居住区规划设计标准(GB50180-2018). 2018.]

[4]
Wei Wei, Hong Mengyao, Xie Bo. Demand-supply matching oriented 15-minute community life circle demarcation and spatial optimization, Wuhan. Planners, 2019, 35(4): 11-17.

[ 魏伟, 洪梦谣, 谢波. 基于供需匹配的武汉市15分钟生活圈划定与空间优化. 规划师, 2019, 35(4): 11-17.]

[5]
Cheng Rong. Small neighborhood achieves the big article on city life: The process and practice of the continuous exploration of neighborhood planning in Shanghai. Global City Geography+Urban and Rural Planning, 2018(2): 51-56.

[ 程蓉. 小街区成就城市生活大文章: 上海持续探索街区规划的历程与实践. 城市地理+城乡规划, 2018(2): 51-56.]

[6]
Cheng Wenjuan, Yu Zhuo. Research on the configuration difference of public service facilities of 15-minute living circle based on POI:A case study of Wuhan. 2019 China Urban Planning Annual Conference, 2019: 833-841.

[ 程文娟, 于卓. 15分钟生活圈公共服务设施配置差异研究:基于武汉市POI数据分析. 中国城市规划年会, 2019: 833-841 ]

[7]
Zhao Yanyun, Zhang Bo, Zhou Fang. Research on the spatial measurement of "15-minute community life circle" in Beijing based on POI. The World of Survey and Research, 2018(5): 17-24.

[ 赵彦云, 张波, 周芳. 基于POI的北京市“15分钟社区生活圈”空间测度研究. 调研世界, 2018(5): 17-24.]

[8]
Sun Daosheng, Chai Yanwei. Study on the urban community life sphere system and the optimization of public service facilities: A case study of Qinghe area in Beijing. Urban Development Studies, 2017, 24(9): 7-14, 25.

[ 孙道胜, 柴彦威. 城市社区生活圈体系及公共服务设施空间优化: 以北京市清河街道为例. 城市发展研究, 2017, 24(9): 7-14, 25.]

[9]
Editorial Department of Urban Planning Journal. Concept, method and practice: An academic discussion on the core meaning analysis of "15-minute community life circle planning". Urban Planning Forum, 2020(1): 1-8.

[ 《城市规划学刊》编辑部. 概念·方法·实践: “15分钟社区生活圈规划”的核心要义辨析学术笔谈. 城市规划学刊, 2020(1): 1-8.]

[10]
Institutional Finance. The state council issues on adjusting standards for classifying cities. Shanghai Urban Planning, 2014(6): 159.

[ 机构金融. 国务院印发《关于调整城市规模划分标准的通知》. 上海城市规划, 2014(6): 159.]

[11]
Yuan Jiadong, Sun Zhenjie, Zhang Na, et al. Reconstruction of urban region system in China based on daily life circle. Scientia Geographica Sinica, 2005, 25(1): 17-22.

DOI

[ 袁家冬, 孙振杰, 张娜, 等. 基于“日常生活圈”的我国城市地域系统的重建. 地理科学, 2005, 25(1): 17-22.]

[12]
Sun Defang, Shen Shan, Wu Tinghai. Life circle theory based county public service distribution: Jiangsu Pizhou case. Planners, 2012, 28(8): 68-72.

[ 孙德芳, 沈山, 武廷海. 生活圈理论视角下的县域公共服务设施配置研究: 以江苏省邳州市为例. 规划师, 2012, 28(8): 68-72.]

[13]
Shanghai Municipal Planning and Land Resources Management Bureau, Shanghai Planning Review Center and Shanghai Urban Planning and Design Institute. Research and Practice of 15-Minute Community Life Circle Planning in Shanghai. Shanghai: Shanghai People's Publishing House, 2017.

[ 上海市规划和国土资源管理局, 上海市规划编审中心和上海市城市规划设计研究院. 上海15分钟社区生活圈规划研究与实践. 上海: 上海人民出版社, 2017.]

[14]
Liu Jiangde, Xu Leiqing. Research on evaluation of urban street regeneration based on public vision: Cases study of Shanghai. Shanghai Urban Planning Review, 2020(3): 101-108.

[ 刘江德, 徐磊青. 基于公众视野的城市街道更新评价研究: 以上海为例. 上海城市规划, 2020(3): 101-108.]

[15]
Yu Yifan, Zhu Feiyang, Jia Shuying, et al. Research on the assessment of age-friendly community. Shanghai Urban Planning Review, 2020(6): 1-6.

[ 于一凡, 朱霏飏, 贾淑颖, 等. 老年友好社区的评价体系研究. 上海城市规划, 2020(6): 1-6.]

[16]
Chai Yanwei, Li Chunjiang, Zhang Yan. A new time-geography research framework of community life circle. Progress in Geography, 2020, 39(12): 1961-1971.

DOI

[ 柴彦威, 李春江, 张艳. 社区生活圈的新时间地理学研究框架. 地理科学进展, 2020, 39(12): 1961-1971.]

DOI

[17]
Zhou Dailin, Huang Huiming. Community life cycle public facility configuration study based on demand-supply correlation: A case study of Guangzhou. Urban Development Studies, 2019, 26(12): 1-5, 18.

[ 周岱霖, 黄慧明. 供需关联视角下的社区生活圈服务设施配置研究: 以广州为例. 城市发展研究, 2019, 26(12): 1-5, 18.]

[18]
Zhou Xian. Assessing the distribution of public service facilities in unit planning based on the perspective of the 15-minute community-life circle: Evidence from Huangpu district of Shanghai. Urban Planning Forum, 2020(1): 57-64.

[ 周弦. 15分钟社区生活圈视角的单元规划公共服务设施布局评估: 以上海市黄浦区为例. 城市规划学刊, 2020(1): 57-64.]

[19]
Han Zenglin, Li Yuan, Liu Tianbao, et al. Spatial differentiation of public service facilities' configuration in community life circle: A case study of Shahekou district in Dalian city. Progress in Geography, 2019, 38(11): 1701-1711.

DOI

[ 韩增林, 李源, 刘天宝, 等. 社区生活圈公共服务设施配置的空间分异分析: 以大连市沙河口区为例. 地理科学进展, 2019, 38(11): 1701-1711.]

DOI

[20]
Wu H Y, Wang L X, Zhang Z H, et al. Analysis and optimization of 15-minute community life circle based on supply and demand matching: A case study of Shanghai. Plos One, 2021, 16(8): e0256904. DOI: 10.1371/journal.pone.0256904.

DOI

[21]
Chang Fei, Wang Lucang, Ma Yue, et al. Do urban public service facilities match population demand? Assessment based on community life circle. Progress in Geography, 2021, 40(4): 607-619.

DOI

[ 常飞, 王录仓, 马玥, 等. 城市公共服务设施与人口是否匹配? 基于社区生活圈的评估. 地理科学进展, 2021, 40(4): 607-619.]

DOI

[22]
Weng M, Ding N, Li J, et al. The 15-minute walkable neighborhoods: Measurement, social inequalities and implications for building healthy communities in urban China. Journal of Transport & Health, 2019, 13: 259-273.

[23]
Zhao Wanmin, Fang Guochen, Wang Hua. Creating a senior friendly pedestrian space system from life circle viewpoint. Planners, 2019, 35(17): 69-78.

[ 赵万民, 方国臣, 王华. 生活圈视角下的住区适老化步行空间体系构建. 规划师, 2019, 35(17): 69-78.]

[24]
Zhang F, Li D Z, Ahrentzen S, et al. Assessing spatial disparities of accessibility to community-based service resources for Chinese older adults based on travel behavior: A city-wide study of Nanjing, China. Habitat International, 2019, 88: 101984. DOI: 10.1016/j.habitatint.2019.05.003.

DOI

[25]
Berge C. Two theorems in graph theory. PNAS, 1957, 43(9): 842-844.

PMID

[26]
Cooper L. Location-allocation problems. Operations Research, 1963, 11(3): 331-343.

DOI

[27]
Hakimi S L. Optimum locations of switching centers and the absolute centers and medians of a graph. Operations Research, 1964, 12: 450-459.

DOI

[28]
Church R, ReVelle C. The maximal covering location problem. Papers of the Regional Science Association, 1974, 32(1): 101-118.

DOI

[29]
Balinski M. Integer programming: methods, uses, computation. Management Science, 1965, 12: 253-313.

DOI

[30]
Levy J. An extended theorem for location on a network. Journal of the Operational Research Society, 1967, 18(4): 433-442.

DOI

[31]
Barilan J, Kortsarz G, Peleg D. How to allocate network centers. Journal of Algorithms, 1993, 15(3): 385-415.

DOI

[32]
Khuller S, Sussmann Y J. The Capacitated K-Center Problem. Berlin: Springer, 1996: 152-166.

[33]
Current J R, Storbeck J E. Capacitated covering models. Environment and Planning B: Planning and Design, 1988, 15(2): 153-163.

DOI

[34]
Geoffrion A M, Graves G W. Multicommodity distribution system design by benders decomposition. Management Science, 1974, 20(5): 822-844.

DOI

[35]
Marianov V, Serra D. Location Problems in the Public Sector. Berlin: Springer, 2002: 119-150.

[36]
Daskin M S, Dean L K. Location of health care facilities//Brandeau M L, Sainfort F, Pierskalla W P (eds). Operations Research and Health Care. Boston: Springer, 2004: 43-76.

[37]
Zhai Shiyan, He Xinxin, Kong Yunfeng, et al. Measuring the spatial accessibility of public services by optimal supply-demand allocation. Acta Geographica Sinica, 2022, 77(4): 1028-1038.

DOI

[ 翟石艳, 何新新, 孔云峰, 等. 基于最优供需分配的公共设施空间可达性分析. 地理学报, 2022, 77(4): 1028-1038.]

DOI

[38]
Kong Y F, Zhu Y F, Wang Y J. A center-based modeling approach to solve the districting problem. International Journal of Geographical Information Science, 2019, 33(2): 368-384.

DOI

[39]
Başar A, Çatay B, Ünlüyurt T. A taxonomy for emergency service station location problem. Optimization Letters, 2012, 6(6): 1147-1160.

DOI

[40]
Boonmee C, Arimura M, Asada T. Facility location optimization model for emergency humanitarian logistics. International Journal of Disaster Risk Reduction, 2017, 24: 485-498.

DOI

[41]
Guo J N, Du Q, He Z G. A method to improve the resilience of multimodal transport network: Location selection strategy of emergency rescue facilities. Computers & Industrial Engineering, 2021, 161: 107678. DOI: 10.1016/j.cie.2021.107678.

DOI

[42]
Cui J, Hu B, Chen S Z. Resource allocation and location decision of a UAV-relay for reliable emergency indoor communication. Computer Communications, 2020, 159: 15-25.

DOI

[43]
Ndiaye F, Ndiaye B M, Ly I. Application of the P-Median problem in school allocation. American Journal of Operations Research, 2012, 2(2): 253-259.

DOI

[44]
Daskin M S, Owen S H. Two new location covering problems: The partial P-center problem and the partial set covering problem. Geographical Analysis, 1999, 31(1): 217-223.

[45]
Nozick L K. The fixed charge facility location problem with coverage restrictions. Transportation Research: Part E, 2001, 37(4): 281-296.

DOI

[46]
Vasko F J, Newhart D D, Stott K L, et al. A large-scale application of the partial coverage uncapacitated facility location problem. Journal of the Operational Research Society, 2003, 54(1): 11-20.

DOI

[47]
Gandhi R, Khuller S, Srinivasan A. Approximation algorithms for partial covering problems. Journal of Algorithms, 2004, 53(1): 55-84.

DOI

[48]
Eiselt H A, Marianov V. Foundations of Location Analysis. New York: Springer, 2011

[49]
Laporte G, Nickel S, Gama F S D. Location Science. Berlin: Springer, 2015: 21-45.

[50]
Kong Y. A matheuristic algorithm for the single-source capacitated facility location problem and its variants. ArXiv: 2112. 12974, 2021: 30.

[51]
Jacobsen S K. Heuristics for the capacitated plant location model. European Journal of Operational Research, 1983, 12(3): 253-261.

DOI

[52]
National Health Commission of the People's Republic of China. Standard of service capacity of community health service centers (2018 edition) 2018-08-22.http://www.nhc.gov.cn/jws/s7882/201809/d77cd05877b84909b0bd0e8b92a3e5f8.shtml, 2018-08-22.

[ 中华人民共和国国家卫生健康委员会. 社区卫生服务中心服务能力标准(2018年版)http://www.nhc.gov.cn/jws/s7882/201809/d77cd05877b84909b0bd0e8b92a3e5f8.shtml, 2018-08-22.]

Options
文章导航

/

〈 〉