1 引言
作为世界最复杂的开放巨系统之一,城市的空间结构及其演变过程具有多样性、随机性、混沌性的特点[1]。以社会学、经济学、地理学为主的学术界、以政府为主导的规划界,向来关注城市富含上述特征的宏、中、微观层次的多要素耦合、多进程的协同发展。比较而言,城乡规划学、建筑学较关注生活小区级及以下空间尺度的各种详规。经济地理学则常把区县级、亚区级、乡镇街道级、村庄/社区级(简称村社级)空间作为传统的宏、中、微观研究尺度,并认为对生活小区级以下空间尺度的研究更偏于工程技术的视角,进而常忽视对该尺度区间的研究。实际经济地理的乡镇街道级、村社级、居委会级空间,基本与城乡规划学居住区级、居住小区级、生活小区级的空间范围相一致,是两者分析空间规律性变化的主要尺度。但不可否认,在发展水平、人口规模相异的不同城市,其尺度较小的30~150 m级空间,即院落组级、街坊级乃至居委会级空间(院落级空间常因小于30 m×30 m的精度而分析难度较大),又常具有相似的外在发展景观,故并不能排除居委会级及以下空间演变的规律性[2-3]。
实际由多个尺度复合而成的城市空间,常具有联系的便捷性(系统科学称为小世界性)、等级的分异性(基本函数为幂函数)、事物的相似性(相互模仿的无尺度现象)等复杂特征。有学者分别从城市的异速生长[4⇓⇓⇓-8]、空间演变的1/f噪声[9⇓⇓-12]、Zipf规律[9-10]、分形现象[1,13 -14]等视角分析了城市的成长机制、时空演变特征,并利用CA、仿生数学等技术对其进行了演变情景的模拟[15-16]。然而在上述研究中,唯有对30~150 m尺度的分析鲜有涉及。实际这一空间尺度对城市居民、企业、机关单位的生产、生活活动尤为重要。相较于区县级(宏观尺度)—乡镇街道级及村社级(中微观)空间尺度,30~150 m空间尺度上多为居民、店铺、微小企业所占用的院落组级、街坊级、居委会级空间,其承载的社会经济活动的市场驱动色彩明显,是以往城市规划、区域规划、土地规划常顾及不到的空间层次或尺度区间。所以对这一尺度区间的空间特征、运行机制的研究,及对该尺度区间中重要区位、关键节点的确认,在当前着力进行国土空间规划的背景下,其现实意义是非常显著的。
2 理论基础
2.1 基层空间及其空间范围
目前中国城乡过渡带的居委会级空间,主要包括在空间上相互交织的住宅小区(如新建的市民小区)、居住组团(如城中村)两种形式。其中住宅小区的居民户数(约300~800户)基本可归为一个居委会的管理规模;居住组团的用地规模差异较大,但也可划分为若干居委会的空间管理范围[23]。据此本文选择居民日常生活的出行半径、商店的最大服务半径150 m为空间数据的尺度上限(基本对应于一个城郊居委会的空间管理范围)[23],并参考对居委会的习惯称谓、区别于传统的城市微观空间(村社级或居住小区级空间)称谓,把30~150 m的斑块尺度称为基层空间尺度,称院落组级—居委会级空间为基层空间。由此城乡过渡带的基层空间,就可具体化为居民日常生活的空间尺度范围,或商店的服务范围、居委会的管理范围了。
与建成区相比,城乡过渡带基层空间的二维属性明显,基本可直接利用空间影像数据进行多重分形分析。但目前提取承载不同社会经济属性的城乡过渡带多种土地子类的信息还比较困难,加之各土地子类耦合的复杂机制也未厘清。故本文只依二维网格分形技术提取了郑州、杭州、北京基层空间建设用地这一大类(不分子类)的土地斑块,并依双对数函数(等价于幂律)提取了拟合曲线的直线部分,进而框定了呈现空间多重分形特征的斑块主要分布区——3个都市的城乡过渡带(分析过程见4.1.1)。在这一地带,小于30 m尺度的建设用地斑块因其离散性较强很难形成多重分形特征,加之受现有计算机运算能力的限制,未被纳入到本分析之内[2-3,13]。即在一个较大的区域(如都市)范围内,远郊零星分布的散户住宅、路口式商店、基础设施(如公交站点)的建筑规模,一般都会低于30 m×30 m尺度,进而对3个都市空间演变(非社会经济发展)的影响有限。如再抛开因建设用地几乎完全被覆盖而在二维空间很难拓展的城市建成区,3个都市的二维多重分形特征分布区基本就对应于空间变化最显著、城乡功能冲突最集中的地带——城乡过渡带[17-18]。简而言之,因城乡过渡带属城市二维多重分形特征的主要分布区,对3个都市30~150 m尺度二维空间的多重分形分析,反映的就是都市城乡过渡带中居委会级及其以下多种空间尺度建设用地的拓展情况。
2.2 基层空间的尺度划分
在网格分形中,多重分形系统常依空间尺度的大小进行划分,故2.1所述的基层空间就应进行进一步的尺度划分。参考城乡规划,本文把居住区级中的扩大小区(对应乡镇街道级空间)看作是城乡过渡带的中观尺度空间(约1000~1500 m),如城郊沿道路开发的片状空间;基础设施较为完善的居住小区级(村社级)空间(主要道路的间距,约300~800 m)看作是其微观尺度空间[23]。于是城乡过渡带的基层空间就指向了居委会管理范围内、不大于支路交叉口间距约30~150 m的空间尺度,并可由大到小细分为居委会级、街坊级、院落组级3种空间尺度(这一划分与网格分形的等级划分大致对应)。在城乡过渡带,这一尺度的地理事物多为企事业单位、集体、店铺、个人所占用、开发的土地斑块。与规划导向的宏中观事物不同,基层空间的市场驱动、利益导向明显。以往中国经济地理的研究多基于宏中观视角,对这一都市基层、并依“市场原则/自下而上的原则”演变的实体空间的特征、现状和机制的研究还很少[1,17,21]。由此对这一不同于城市宏中观空间(如区县级、亚区级、乡镇街道级)演变机制的研究(微观空间(村社级空间)常因同时受规划、市场影响,而多呈无显著规律性的混沌态[8,17⇓⇓⇓⇓ -22]),将有可能揭示这一常被忽视、但又重要的城市成长机制。
2.3 多重分形特征的数理基础
理论界已明确,源于复杂理论的异速生长和熵理论,是解释空间多重分形产生并描述其数理特征的有力工具[1]。
综上所述,都市区域出现以空间增长为主的多重分形特征,须满足两个条件:具有以发展要素异速生长为基础的运行机制;空间演变上形成蕴含一定规律性特征的“混乱性”,即熵情。即空间多重分形分析是与异速生长分析、香农熵的分析相辅相成的。
2.4 分析技术简介
本文采用的具体多重分形方法为网格分形技术。它以网格边长为1/2向下级逐级迭代(初始级为m = 0),从而下级空间层次的空网格加非空网格的数量为上级的4倍,由此会带来在迭代一定次数后数据计算的快速增加。而本文对都市城乡过渡带的分析,将实现数据计算量、空间分析精度的提高:首先,受计算机硬件影响,已有研究多计算到网格分形的第八、九级空间(m = 7、m = 8,为迭代次数),即分析到了16384个、65536个网格的斑块数量[27⇓-29]。由表1可知,3个都市空间尺度都处于40~150 m之间,这对应于郑州、杭州、北京主体范围的第九、十级空间[19⇓⇓-22]。其中第十级的网格数量已达262144个,从而实现了计算量的增加。其次,与前者相关联,对郑州特定区域、杭州主城区、北京六环内建设用地的多重分形分析,将选取较宏中观空间更为精细化的基层空间作为本文的研究对象。具体地,在网格分形划分到第九、十级时,郑州、杭州、北京的空间尺度已降到如表1“选取的空间尺度”一行的尺度范围,这是以往都市研究很少涉及的空间尺度。但由表1该尺度提取的具体数据可看到,城市基层空间常规的30~150 m空间尺度,在这3个都市只能精确到第九、十级40~150 m的空间尺度。如此介于30~40 m尺度的斑块会被剔除在本分析之外。但这一尺度相邻两个斑块在上一尺度又会被合并到一个大斑块中,进而其部分信息也可被提取出来。所以都市城乡过渡带空间系统的空间标度区虽有所丧失,但不会丧失主要信息,仍有很强的代表性。
表1 研究都市概况与数据分析的空间尺度及年份
Tab. 1
| 发展背景空间演变总体特征 | 郑州 | 杭州 | 北京 | ||
|---|---|---|---|---|---|
| 国家大中城市的中端位置 | 国家大中城市的上端位置 | 国家大中城市的顶端位置 | |||
| 集聚型的传统性特大城市 | 离散型+集聚型的现代化特大城市 | 集聚型的超大城市 | |||
| 空间尺度 | m = 8 | 148.52 | 82.03a | 101.56ᵇ | - |
| m = 9 | 74.26 | 41.02a | 50.78ᵇ | 103.91 | |
| 数据年份 | 1988 | 1995 | 1985 | ||
| 1995 | 2000 | 1999 | |||
| 2006 | 2005 | 2008 | |||
| 2015 | 2010c | 2015 | |||
注:a为1995和2000年数据,b为2005和2010年数据,c 2015年以后3个都市(含杭州2015年)空间数据的拟合均不理想,故分别以2010年和2015年做为三者2010年代的代表年份;进一步解释见第3部分最后一段。
3 案例区选择及其基础数理分析
3.1 案例区选择
依第七次全国人口普查数据,郑州、杭州与北京分属中国的特大城市和超大城市,且1990年代以来3个都市快速发展的机制和现状也明显不同(表1)。毋庸置疑,三者的空间演化均蕴含着基础性、共通性的城市演变规律,规划、市场力量在其空间总体变化中也会产生不同的影响。具体到40~150 m的都市城乡过渡带的基层空间,演变的基本驱动力为市场机制。在这一空间尺度,个体的主观性、利益驱动的概率性均较强,不属于规划力量的主要影响区间(但也会受后者的影响)。进一步结合对中小城市30~150 m空间尺度的研究可认为[30],无论都市还是中小城市,在这一空间尺度都显示出与宏中观空间尺度不同的演变特征。由此对它的研究抑或发现未被重点关注的“自下而上”的城市成长机制。
人们的直观感觉都指向一个现象:都市基层空间所具有的特征,都处于被宏中观空间所主导的情景之下。于是在粗粒化思想指导下[24],本文还将分析城乡过渡带的基层空间与宏中观空间的融合情况,以探究其自身演化是否属于与后者相匹配的适应性变化。其目的,就是要描述基层空间的城市发展规律和空间运行机制,丰富对“市场原则/自下而上的原则”、“规划原则/自上而下的原则”两种成长机制及其耦合的认识。这有助于发现不同发展背景下都市局部空间的演变特征、演变规律,深化对都市基层空间的认识。
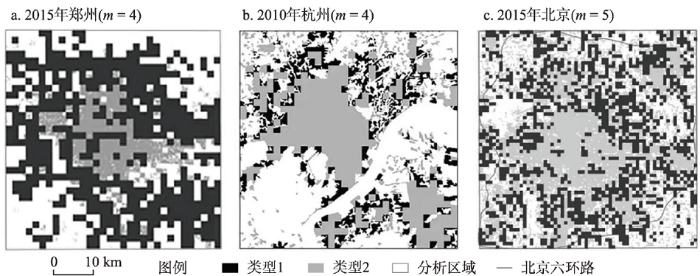
各都市都有不同的空间规模,故基于网格分形提取的郑州、杭州、北京各级网格的边长也存在差异(见表1“空间尺度”)。于是依建设用地密度基本趋同的原则,本文选取了相应的区域范围,分别为38.02 km2(郑州)、21.0~26.0 km2(杭州主城区)、53.2 km2(北京),参见图1(可视为各城市万花筒式空间结构的“二维码”标识)。进而与城市规划、经济地理研究中各级空间尺度相对应,41.02 m(杭州)、50.78 m(杭州)附近的空间尺度,因贴近城郊多个相邻院落的分布空间,本文称之为院落组级空间尺度;74.26 m(郑州)、82.03 m(杭州)、101.56 m(杭州)、103.91 m(北京)附近的空间尺度,称之为街坊级空间尺度;而148.52 m(郑州)的空间尺度为居民日常生活的范围,称之为居委会级空间尺度。而这些空间尺度正好位于城市最基层约30~150 m的空间系统之内。由此,3个都市40~150 m的空间尺度(对应m = 8、m = 9)得以具体化。而以下对这一空间尺度的分析,将深化人们对周围院落组级、街坊级、居委会级空间格局的直观感受。
图1
图1
研究都市具体范围
注:m为空间尺度,代表不同空间精度。
Fig. 1
The schematic diagrams of specific research scope of three metropolises
3.2 支撑性分析
表2 研究都市香农熵值的比较
Tab.2
| 时间和空间等级 | 郑州 | 杭州 | 北京 | |
|---|---|---|---|---|
| 年份1 | m = 8 | 9.080741(1988) | 10.040457(1995) | 10.060973(1985) |
| m = 9 | 9.386748(1988) | 11.326567(1995) | 11.319680(1985) | |
| 年份2 | m = 8 | 9.651591(1995) | 10.111827(2000) | 10.749777(1999) |
| m = 9 | 9.996349(1995) | 11.402379(2000) | 12.036636(1999) | |
| 年份3 | m = 8 | 9.662968(2006) | 10.364874(2005) | 10.699211(2008) |
| m = 9 | 10.02373(2006) | 11.692792(2005) | 2.666682(2008) | |
| 年份4 | m = 8 | 10.14634(2015) | 10.508022(2010) | 10.752167(2015) |
| m = 9 | 10.45729(2015) | 11.826962(2010) | 12.039661(2015) | |
注:括号内为香农熵值对应的年份。
3.3 数据选取和分析过程
对3个都市具体案例区的分析涉及到对斑块密度层次(q)的选取,并会聚焦于空网格、非空网格交汇的区域、偏于城乡二维属性的交汇区——城乡过渡带。由多重分形参数的定义,q是常用来表示斑块密度大小的一个参数,q越小越指向对高密度空间的解析,反之则指向低密度空间的解析[27⇓-29]。在实际操作中,3个都市各级q值全被限定在[-2.0, 13.0]的区间。把下限值设在-2.0,是避免把对下一级空间尺度(如m = 9)的分析越级到上一级(如m = 8)。同时,本文本无意对q上限设定阈值,因它可反映某一尺度更全面、精细的空间结构;但受计算机硬件的限制,还是设定了13.0的上限值。由此,[-2.0, 13.0]的q值区间不仅保证了低密度区中具有多重分形特征的网格分布区的广泛存在,也剔除了q<-2.0的建成区高密度区的网格。该分析过程的具体示例可参见4.1.1中对郑州的分析。
于是基于规范的多重分形分析程序[31⇓⇓-34],本文获得了上述空间尺度随q值变化而产生的总体演变强度(广义相关维数Dq)、系统统计学特征(质量指数τ(q))两个全局性指标,系统的局部特征(奇异性指数a(q))及随之变化的局部分维值(f(a))两个局域性指标,并绘制了Dq-q、τ(q)-q、a(q)-q、f(a)-q、f(a)-a(q)曲线拟合示意图(详见第4部分)。进一步,还进行了主要分维值(如D0、D1、D2)、参数(如a(q)、f(a))取值范围、统计学属性(τ(q)-q的曲线形状)的分析;并通过对多分维谱(即f(a)-a(q)曲线)谱偏、峰值、谱宽等的界定与判断,来掌握城乡过渡带的空间变化是以什么样的q值为主、其演变的主导性和主体性(区间)如何、演变的复杂程度等情况[1,3,13,29,31,34]。其中对局部演变特征(如a(q)、f(a)、f(a)-a(q)曲线)的解析,又可具体描述城乡过渡带不同空间尺度上的细节变化,这对本文又尤为重要。于是随着q值的变化,3个都市城乡过渡带基层空间的复杂空间特征将被逐步解析出来。
需要说明的是,由于城市发展进程(如房地产调控、基础设施建设)的变化,2015年以后(含杭州2015年)空间数据的异速生长分析、熵值分析并不理想。故基于定性认识、定量分析相结合的视角,对各时间段典型年份的选择如表1“数据的年份”所示。
4 都市城乡过渡带基层空间系统的发展演变
本部分将沿传统性特大城市→现代化特大城市→超大城市的方向,以郑州、杭州、北京的城乡过渡带为案例区,对表1中1980年、1990年、2000年、2010年代的多个空间尺度(m值为8~9或m值为7~8)展开分析,以探究多重分形特征在混沌的基层空间各尺度中有、无、似有似无之间转换的规律。
对3个都市基层空间的分析,主要包括以下内容:第一,有典型多重分形特征的m等级及其空间标度区,进而进行区域空间自组织情况的判断。第二,有多重分形特征的各空间尺度的q值范围,以反映该空间特征分布的密度区大小及其q值分布。第三,各q值分布区的空间演变强度(Dq)。第四,因不同时满足两个指标系统而产生的广义多重分形子系统的构成情况;特别是对典型、广义f(a)-a(q)曲线(见4.1.3)的信息提取。其中对第四个问题的分析又可具体到每个空间等级m的f(a)-a(q)曲线,以期反映:① 该基层空间曲线与其它m级曲线的位置关系,以掌握空间总体的驱动力构成。又包括:首先,该f(a)-a(q)曲线是否为其它曲线所包围或相互交叉,以反映基层空间的适应情况;其次,自下而上的市场机制、自上而下的规划机制在系统内的匹配关系。② f(a)-a(q)曲线的谱偏、谱宽、形态的规则性、多条曲线是否相似等具体信息;这些信息都有助于辅助以上信息,并得出相应结论[27⇓⇓⇓⇓⇓-33]。
总之,基于多重分形技术的分析过程和判断依据虽显琐碎,但却是3个都市城乡过渡带精细化分析的科学依据。以下将逐一进行分析。
4.1 郑州城乡过渡带基层空间系统的发展演变
4.1.1 多重分形特征的网格范围及其q值区间的选取
对于不同空间尺度的q值范围都有一个具体的选取过程,即要求在做多重分形分析之前进行一个lg(网格序号)-lg(斑块数量)的双对数曲线拟合(等价于幂律分析)[1]。因空间精度越大,该曲线的阶梯性越强(即含相同斑块数量的网格越多),故本文以2006年数据为例拟合了m值为5~9在[-2.0, 13.0]q值区间的双对数曲线(图2a~2e)。可见,m = 5的拟合效果明显大于m值6~9的拟合效果,故以下以图2a为重点展开示例分析。由图2a可见,右下侧小q值区间(斑块数量排前135位的网格)的拟合曲线,左上侧大q值区间(第599~801位的网格)的拟合曲线,都未被纳入到多重分形的q值取值区间。由拟合优度(R2)为0.9517时的取值区间可知,真正具有多重分形特征的网格只分布于约第136~598位的网格范围(m = 5全部网格为1024个,其中第802~1024位为空网格)。溯源可查,在空间精度为30 m情况下,m = 5的多重分形特征区大约位于建设用地覆盖比例为63%~5%的网格内(此即聚焦于城乡过渡带的原因)。建设用地的高密度区(小q值区,建成区)、极低密度分布区(大q值区,传统乡村)并不具有典型多重分形特征。虽然m = 5尺度的斑块范围并不能完全代表m值为8~9范围,却为其框定了一个大致区域;而累次拟合就趋于逼近有多重分形特征的分布范围。由此,城乡过渡带基层空间所含建设用地斑块的具体范围(见3.3)就得以明确。从3个都市的具体分析结果看,城乡过渡带才是二维多重分形特征发生的主要区域(依推理,三维多重分形分析应会更科学揭示建成区立体空间的复杂性。但因三维数据、多子类斑块数据目前难以同时获得,加之三维耦合性空间会更复杂,故本文不做讨论)。
图2
图2
基于双对数曲线的空间多重分形特征分布范围的选择
注:以郑州2006年的数据为例;图a中满足双对数函数的数据段用蓝色曲线表示,否则用灰色曲线表示;图b~e未做此处理。
Fig. 2
Distribution range analysis of spatial multifractal characteristics based on double logarithmic curve
4.1.2 全局性、局域性指标分析(以1995年为例)
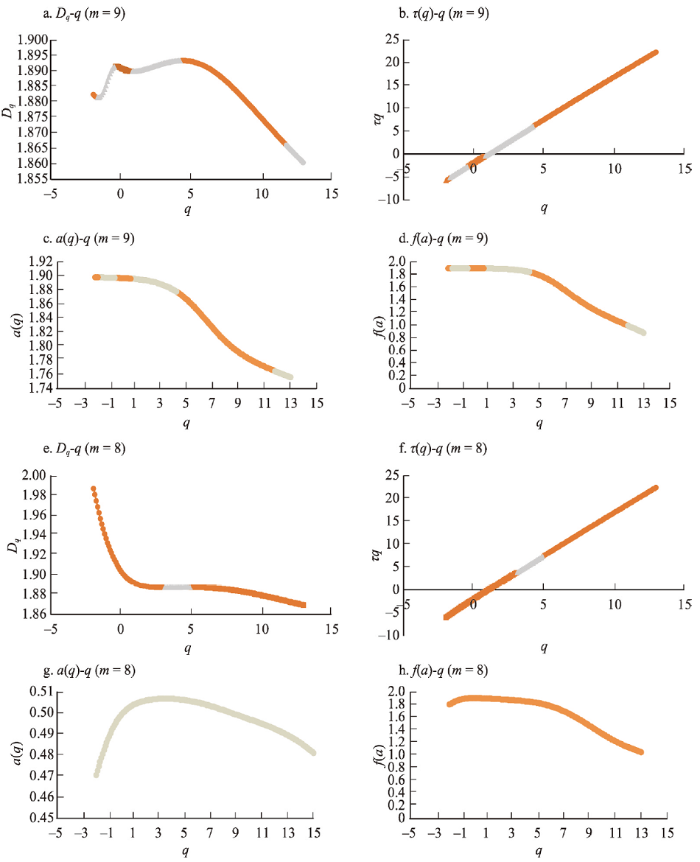
q值范围的选取以2006年为例,指标性分析则以1995年为例。典型空间多重分形系统需同时满足全局性、局域性指标体系。基于分析程序,本文获得了3个都市4年多空间尺度的Dq-q、τ(q)-q、a(q)-q、f(a)-q、f(a)-a(q)曲线(图3),并进行了指标汇总(表3)。把其中的空间尺度具体到3个都市的基层空间系统,就可得到相应的分析结果。而对于只满足一个指标系统的空间子系统,则对应于广义多重分形系统[22]。上述各拟合曲线常呈现非经典的规则形状(图3、图4),这是因为经济地理系统是复杂系统,在典型空间多重分形特征之外会有一个敏感且多变的特征过渡区或趋势化特征分布区[22]。本分析不仅可以得到标识典型多重分形特征的各种曲线的典型性,也可辨识特征过渡区(即不含典型特征的广义多重分形特征分布区)的存在(图3、图5中彩色曲线段及对图4、图6中典型、广义f(a)-a(q)曲线的对比)。
图3
图3
郑州典型、广义多重分形的多种指标拟合示意
注:图中满足多重分形条件的曲线段用黄色曲线表示,不满足多重分形条件的曲线段则用灰色曲线表示。
Fig. 3
The schematic diagrams of Zhengzhou's fitting curves for various indices of typical, generalized multifractals
表3 郑州基层空间系统多期建设用地的典型多重分形指标
Tab. 3
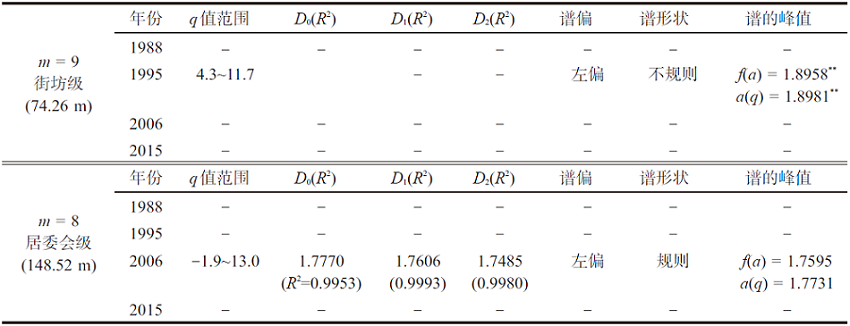 |
注:“-”表示不满足多重分形条件;**在广义多分维谱条件下的峰值,现实中并未形成该峰值。
图4
图4
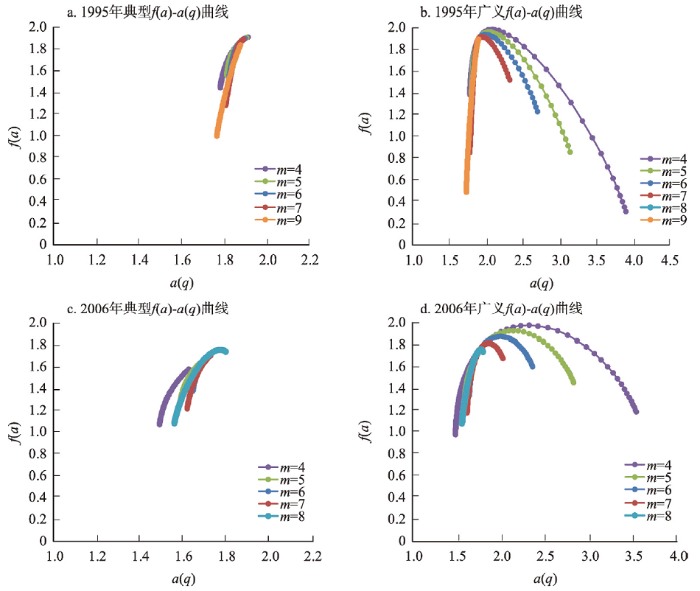
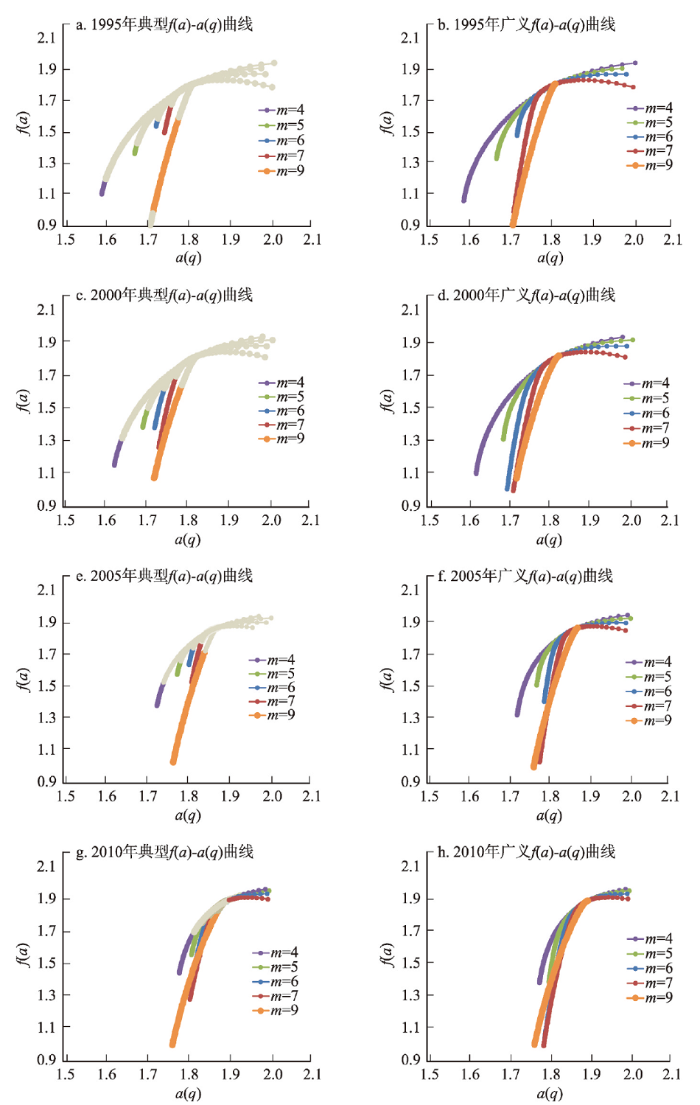
1995年和2006年郑州的典型、广义f(a)-a(q)曲线
注:因广义f(a)-a(q)曲线较为密集,各图的横坐标有所变化。
Fig. 4
Typical and generalized f(a)-a(q) curves of Zhengzhou in 1995 and 2006
图5
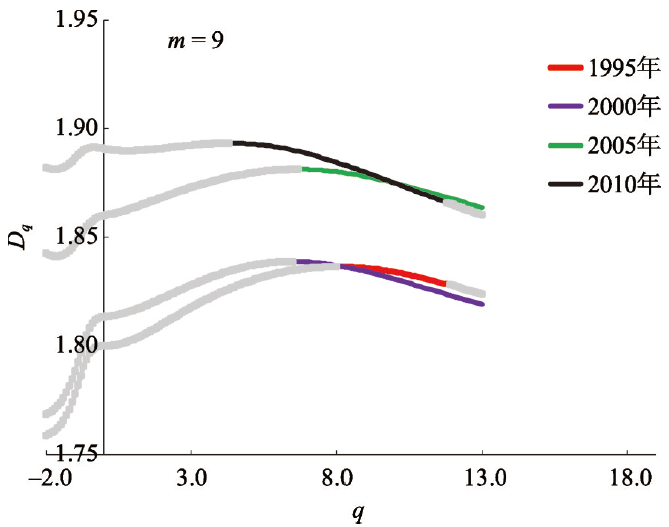
图5
杭州基层空间系统Dq-q曲线
注:满足多重分形条件的数据段用彩色曲线表示,否则用灰色曲线表示。
Fig. 5
Dq-q curves of phases of Hangzhou's grass-roots space subsystem
图6
图6
杭州3个空间子系统的f(a)-a(q)曲线
注:本图较
Fig. 6
f(a)-a(q) curves of Hangzhou's q-value range of three space subsystems
郑州地处传统农业区、周边农村和城市的内部差距较小,外部因素影响较弱,其基层空间的传统性较为明显。本文基于郑州1988年、1995年、2006年、2015年的所选取空间范围的网格数据,进行多重分形分析。以1995年的m = 9(网格边长为74.26 m)、m = 8(网格边长为148.52 m)数据为例(图3),分析获得了基于全局性、局域性q值的Dq-q、τ(q)-q、a(q)-q、f(a)-q曲线,进而对郑州空间系统进行了q值分布范围、演变特征、统计学属性的判别。为提炼郑州基层空间系统的基本存在态势、对比4期的演变特征,列出q值范围、典型Dq值、拟合优度(R2)、f(a)-a(q)曲线的主要分析指标等(表3),得到如下结论:
首先,在城乡过渡带的基层空间,郑州只在1995年街坊级(m = 9)、2006年居委会级(m = 8)的空间产生了典型多重分形特征。其他年份该空间尺度则处于混沌或无序状态,并未同时满足全局性、局域性多重分形指标。如1995年m = 8的f(a)-q曲线(图3d)因a(q) < 1不符合取值要求,从而不具备典型多重分形特征。
其次,在1995年的街坊级(m = 9)空间,仅在q值为[4.3,11.7]区间段、而非[-2.0, 13.0]的整体区间产生了典型多重分形特征。在2006年居委会级(m = 8)空间,出现多重分形特征的q值扩大到[-1.9, 13.0]空间(但这并不代表它是全域空间分布)。
另外,如以q ≤ 0、q ≥ 3作为划分建设用地高、中、低密度区的界限,则郑州一般只在基层空间的中、低密度区出现多重分形特征,并在该密度区上承载着多种演变强度(Dq)的空间变化。例如在1995年郑州街坊级(m = 9)的空间,q值为[4.3,11.7]的区间形成了多重分形特征,且其演变强度横贯高、中、低值区(表3)。
综上所述,对郑州基层空间演变特征、演变过程的基本认识可表述为:该空间属前分形系统,并未产生多年期连续的、全域q值的、多尺度上的多重分形特征;基层系统只在特定年份的特定空间尺度及其局部q值区间,产生了演变强度各异的多重分形特征。
4.1.3 多分维谱分析
绘制并比较1995年、2006年多重分形系统的多分维谱(即f(a)-a(q)曲线,图4),有助于描述郑州基层空间系统的谱宽、谱偏、分维谱形状、峰值等更为细致的空间演变。图4a、4c是现实空间中真正形成典型多重分形特征的f(a)-a(q)曲线,本文谓之典型f(a)-a(q)曲线;图4b、4d则是广域q值的f(a)-a(q)曲线,是包含规律化多重分形系统(即同时满足全局性和局域性指标的典型多重分形系统)、趋势化多重分形系统(只满足一个全局性或局域性指标)及无序化系统(都不满足两个指标)的广义空间多重分形系统,是广域q值([-2.0, 13.0])分布区[22]。即广义多重分形系统可看作是由规律化多重分形子系统、趋势化子系统、无序化子系统相复合而成的,图4b、4d为其多分维谱,谓之广义f(a)-a(q)曲线。而对广义f(a)-a(q)曲线图4b、4d的解析,将为深入了解典型f(a)-a(q)曲线图4a、4c并识别典型多重分形特征的影响范围提供佐证和参考。
进一步结合由上述分析所得的q值范围、Dq值的变化、各子系统的统计学属性及奇异性(a(q))、局部分维值(f(a))等信息,可得到各m系统的相应结论。由此在确定1988年、2015年郑州基层空间并未形成多重分形特征的情况下,汇总1995年、2006年的f(a)-a(q)曲线图(图4)发现:
首先,郑州基层空间系统的f(a)-a(q)曲线基本处于其它空间尺度曲线的中下端。具体地,郑州街坊级、居委会级空间的该曲线,基本处于亚区级—乡镇街道级曲线(m值为4~6)的覆盖之下,与村社级(m = 7)则有交叉。即郑州基层空间基本为宏观空间所支配,但却与中观空间属同等的并列关系。这表明,郑州基层空间的演变虽属适应性变化,但在空间格局中的作用却已很强,一般的基层空间为中观空间严重影响的情况在郑州并未显著发生。
由表2可知,1990—2010年代郑州的快速发展,在1995年街坊级、2006年居委会级空间形成了典型多重分形特征。但郑州在总体发展过程中,它的基层空间(包括未获得数据的院落组级空间)整体还处于混沌状态,并具有一定的无序性。
由以上分析可知,郑州基层空间的整体发展虽受宏中观空间一定的影响,但其市场驱动的特点却更明显。该基层空间整体以混沌态为主,但多重分形特征时隐时现,这已成为郑州基层空间演变的重要特征。
4.2 杭州城乡过渡带基层空间系统的发展演变
杭州是发达省份浙江的省会,是和传统性特大城市郑州在宏中观领域发展相异的现代化特大城市。其市场驱动下的个体私营经济、电子商务在全国处于前列,基层空间的产业发展、城市化发展也都较郑州为快。但受地形、河流、城市规划的影响,杭州宏观上也呈现了沿杭州湾类飞地式的发展。而以下分析的就是杭州主城区的基层空间在这种背景下的空间变化。
4.2.1 全局性、局域性指标分析
表4 杭州基层空间系统多年期建设用地的多重分形指标汇总
Tab. 4
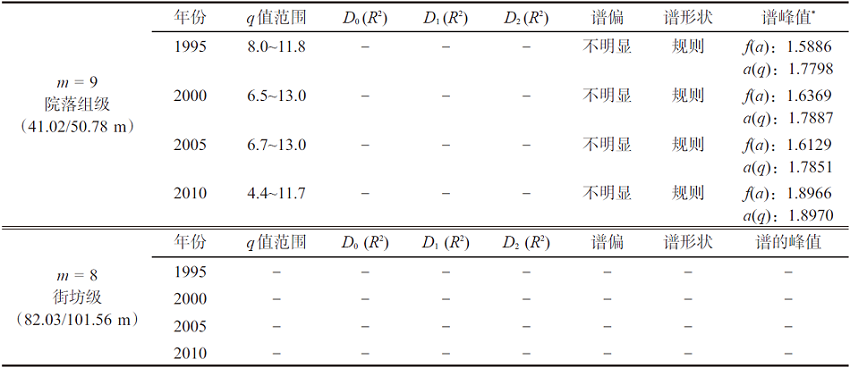 |
注:“-”表示不满足多重分形条件;*广义f(a)-a(q)曲线的峰值,现实中并未形成该峰值。
首先,杭州基层空间的多重分形特征只出现在了m = 9(41.02/50.78 m)的院落组级空间,m = 8(82.03/101.56 m)的街坊级空间在4个年份从未出现该特征。分析显示,杭州多重分形特征只出现在了m值4~7与m = 9两个空间尺度区间,这分别对应典型的自上而下/规划、自下而上/市场的两个驱动力作用区间(无尺度区间)。且该特征在研究期很稳定。其次,杭州基层空间的多重分形特征只出现在了建设用地低密度区,这源于个体私营经济的快速发展,带动了郊区院落组级(m = 9)建设用地的外拓。而街坊级(m = 8)建设用地则整体处于混沌状态,进而未形成多重分形特征。
但近几十年来,杭州主城区基层空间的q值范围一直有向中密度区拓展的趋势,如院落组级(m = 9)的q值范围由1995年的[8.0,11.8]拓展为2010年的[4.4,11.7]。这反映出,随着自下而上的市场机制的驱动,逐步引起了个体私营企业的规模化发展。
4.2.2 多分维谱分析
杭州主城区1995年、2000年、2005年、2010年多空间尺度的f(a)- a(q)曲线示意图如图6所示。从典型、广义空间多重分形特征两个视角看,院落组级空间(m = 9,41.02/50.78 m)子系统的f(a)-a(q)曲线与其它曲线的融合相对较差。但随着时间发展,该曲线逐步向高等级曲线靠近,并出现了曲线的交叉现象。这说明该空间尺度的演变是相对独立的,总体上仍遵循着自己独特的发展规律;但同时,这一曲线出现逐步向m值为4~7的4个空间尺度f(a)-a(q)曲线融合的倾向。与郑州相比,杭州院落组级空间在总体空间的影响更为明显、作用也越来越大。这说明杭州郊区个体私营经济对基层土地利用模式的影响要大于郑州。
4.3 北京城乡过渡带基层空间系统的发展演变
图7
图7
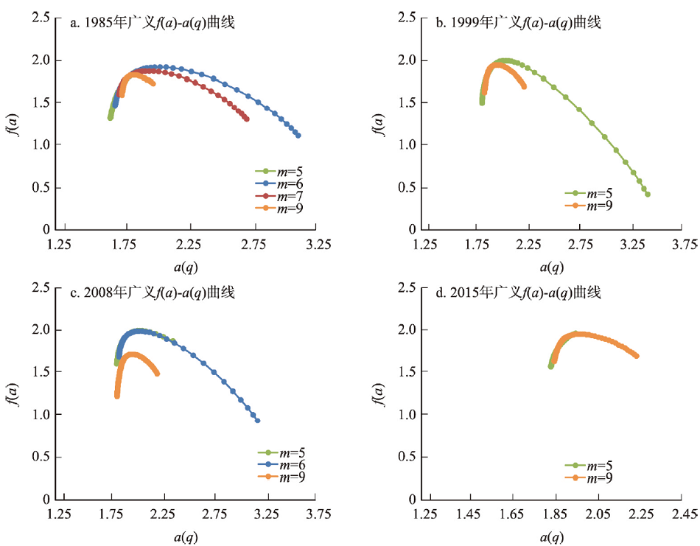
北京3个空间子系统的f(a)-a(q)曲线
注:1985年和2008年的图中m=5的曲线常为m=6的曲线所遮挡。
Fig. 7
f(a)-a(q) curves of the three space subsystems in Beijing
表5 北京基层空间系统多年期建设用地的多重分形指标汇
Tab. 5
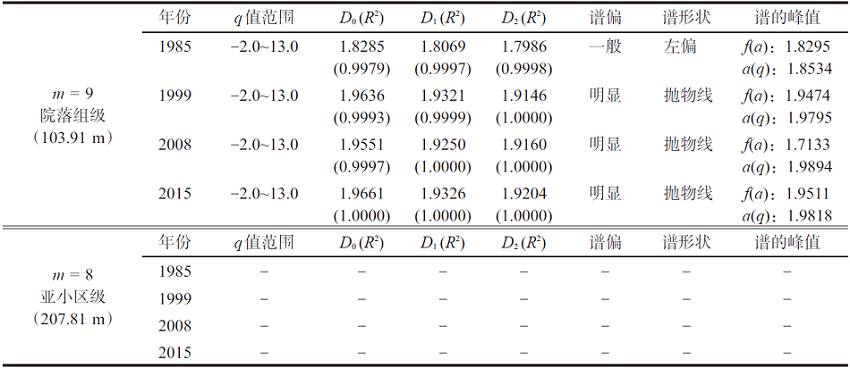 |
注:“-”表示不满足多重分形条件。
首先,北京多空间尺度上的多重分形特征表现不一。在街坊级空间(m = 9),北京3期(2008年不满足香农熵条件)具有多重分形特征,且q值范围都为[-2.0, 13.0]。与郑州、杭州相比,北京基层空间拥有一个更广域的q值分布区间。在宏观空间尺度(m = 5),始终存在规划(自上而下)主导的多重分形特征。在中观空间(m = 6、m = 7),多重分形特征总体趋于消失。在m = 8的空间尺度(约207.81 m),4期全部没有形成多重分形特征,进而形成了一个多重分形特征分布的“断层”。其次,北京m = 9空间的 f(a)-a(q)曲线为更高级别的曲线所包围,即其演变的奇异性(a(q))和局部分维值(f(a))都小于其它空间尺度。结合实际,这说明北京街坊级空间(m = 9)处于其它大尺度空间的辐射之下,整体已和其它空间尺度相融合。第三,北京街坊级空间(m = 9)的Dq值长期处于高值区(1.90~2.00之间),明显高于郑州、杭州的空间演变强度,应是北京40年的快速发展所致。另外,与郑州、杭州相比,北京街坊级(m = 9)空间演变的规律性更强,其多重分形的q值区间为[-2.0, 13.0]全域覆盖。这明显不同于院落组级空间尺度上郑州(m = 9)多重分形特征似有似无、杭州(m = 8)多重分形特征全无的空间格局。
4.4 3个都市城乡过渡带基层空间系统的对比分析
对比3个都市城乡过渡带基层空间的主要特征可看到:郑州基层空间属以混沌态为主、并与宏中观空间有明显差异的系统。其Dq、a(q)、f(a)等参数值偏小,整体属于一个由中小城市向传统性特大城市演化的空间系统。超大城市北京的空间格局虽规模巨大、演变强烈,但其微、中、宏观空间的演变类型却相对简单或形成了相对一致的演变特征,且在街坊级空间形成了广域的、常态化的多重分形特征。比较而言,其基层空间的发展受规划作用较强(甚至可说其基层空间是宏中观空间覆盖之下的“神经末梢”),已与宏观空间融为一体。现代化特大城市杭州在四年期院落组级空间全具有典型多重分形特征;但街坊级空间则完全未形成该特征。这应源于杭州该层级特定社会经济活动占用的土地空间的演变所致。
进一步对比3个都市的街坊级空间可看到:在该空间尺度,郑州呈现了以混沌为主、多重分形特征时有时无的发展状态,杭州完全没有多重分形特征,北京则形成常态化的多重分形系统。单从演变过程看,3个都市基层空间的上述演变状态并没有呈现关联性。就这一点看,空间尺度相近的70~105 m的存在状态似乎最能说明这一问题:多重分形特征在传统性都市郑州街坊级空间(m = 9,74.26 m)似有似无的、在现代化都市杭州街坊级空间(m = 9,82.03/101.56 m)全无的、在集聚型大都市北京院落组级空间(m = 9,103.91 m)全q值区间的分布,代表了3个都市基层空间完全不同的真实存在情况。实际各城市基层空间都有自身独特的演变规律,其演变特征也反映的是在规划、市场差异化作用下、不同城乡融合情景下的具体空间格局变化。或许它们在基层空间社会经济发展的内在机制上有一定的规律可循,但其在空间上的外部“投影”——经济地理空间上却常具有不可复制性。
5 讨论和结论
5.1 讨论
5.1.1 典型和广义f(a)-a(q)曲线
都市城乡过渡带是复杂的前分形系统。由此可把多重分形分析中的典型f(a)-a(q)曲线拓展为广义f(a)-a(q)曲线,进而使之可涵盖典型多重分形特征的过渡区或退化区(如图6中的灰色曲线部分)所指向的空间子系统。其目的,就是要促进对城乡过渡带多类型土地斑块的空间耦合、不同土地斑块密度区(q值区间)演变细节、基层空间总体演变的复杂背景的量化认识,以期更真实地反映典型、非典型多重分形特征相复合下的基层空间演变。
5.1.2 多重分形分析与其支撑性分析
5.2 结论
5.2.1 市场驱动下的都市城乡过渡带基层空间
介于30~150 m尺度的院落组级、街坊级、居委会级空间,构成了城市的基层空间系统。从3个都市带有一定时间维度的多重分形分析看,相较于宏中观空间的规划驱动,市场驱动在基层空间演变中的主导性、主体性更显著,在基层空间区位的形成、空间格局的演变中的作用也更强。这启示,在都市基层空间的规划中,应充分考虑市场的基础性驱动作用,以做好诸如居民购物出行、基层商服网点、交通站点等关键空间节点的合理规划与调整。
本文通过明确各典型、广义f(a)-a(q)曲线的组合关系、相互间的位置差异,乃至对其具体q值曲线段的空间区位溯源,有助于从技术层面确定基层空间演变中的关键节点、规划调整其具体的发展规模、合理配置其不同的发展功能。而从3个都市典型多重分形特征在广义f(a)-a(q)曲线中多处于偏顶点区域的分布来看,上述量化认识及相应措施的实施,对促进3个都市城乡过渡带良性发展的实际效果应更显著、更直接。
5.2.2 都市城乡过渡带非理想化的基层空间及其演变情景
现实中,经济地理空间常处于规律化、趋势化与无序化相复合的演变状态,并会产生与之相对应的复杂空间结构。具体到3个都市建设用地、农业用地二分化的二维基层空间,其城乡过渡带俨然呈现了一个“二维码”式的空间结构(图1)。由此拓展,它还会呈现更复杂的多类型、多尺度复合的二维“万花筒”、三维“拼装积木城市”的形态。可知,都市的基层空间结构复杂而多变,常蕴含着非理想化的空间特征、演变过程。但同时,这种看似混乱的、非理想化的空间结构,常会产生诸如时断时续、似有似无的多重分形特征(分布区)等可识别的演变规律。这就为由非线性视角探究真实的经济地理空间提供了一个切入点。
从分析结果看,当前中国都市城乡过渡带的基层空间并不存在一个依中小城市→传统性特大城市→现代化特大城市→超大城市的必然演替过程。实际各都市在城市体系中具有不同的发展地位,其基层空间社会经济发展的背景与状态也不尽相同,加之地形、河流、文化、制度等的影响,它们的空间结构、演变模式虽可相互借鉴但却不可相互替代。例如处于国家大中城市中端的郑州(传统性特大城市),其基层空间多由低端的非农化、基层的城市化所主导;处于顶端的北京(发达的超大城市),其基层空间则受高端产业化的影响显著。简而言之即,各都市基层空间发展“情景”的差异往往较大,故其数理特征也各有特色。
总体上,都市城乡过渡带的基层空间是以市场驱动为主的复杂空间系统,明显不同于规划驱动为主的宏中观空间系统。而利用多重分形这一逐步逼近空间现实的分析方法,可为以非典型特征及其空间子系统为发展缓冲区的城乡过渡带的空间动态规划、弹性规划,提供非线性的认知视角和全新的技术支持。
参考文献
Fractal dimension versus density of built-up surfaces in the periphery of Brussels
DOI:10.1111/pirs.2007.86.issue-2 URL [本文引用: 2]
Comparing the fractality of European urban neighbourhoods: Do national contexts matter?
DOI:10.1007/s10109-010-0142-4 URL [本文引用: 3]
An analytical process of the spatio-temporal evolution of urban systems based on allometric and fractal ideas
DOI:10.1016/j.chaos.2007.01.130 URL [本文引用: 1]
A novel model for allometric scaling laws for different organs
DOI:10.1016/j.chaos.2005.04.082 URL [本文引用: 1]
Allometric control, inverse power laws and human gait
DOI:10.1016/S0960-0779(98)00149-0 URL [本文引用: 1]
Multi-scaling allometric analysis for urban and regional development
DOI:10.1016/j.physa.2016.08.008 URL [本文引用: 1]
Allometric growth of Beijing development functions from 1979 to 2009: Based on the analysis of the social economy functions
DOI:10.2307/142022 URL [本文引用: 3]
1979—2009年间北京多种发展功能的异速生长: 以社会经济功能为主的分析
Multi-fractal measures of city-size distributions based on the three-parameter Zipf model
DOI:10.1016/j.chaos.2004.02.059 URL [本文引用: 2]
Zipf's law, 1/f noise, and fractal hierarchy
Self-organized criticality: An explanation of the 1/f noise
DOI:10.1103/PhysRevLett.59.381 PMID:10035754 [本文引用: 1]
The chaos of economic geography-"entropy": A review of relevant analytical techniques
经济地理空间的混乱现象—“熵情”: 兼分析技术评述
Introduction to multifractal detrended fluctuation analysis in Matlab
The morphology of built-up landscapes in Wallonia (Belgium): A classification using fractal indices
DOI:10.1016/j.landurbplan.2007.07.002 URL [本文引用: 1]
Modeling urban expansion scenarios by coupling cellular automata model and system dynamic model in Beijing, China
DOI:10.1016/j.apgeog.2006.09.006 URL [本文引用: 1]
Multi-agent systems for simulating and planning land use development
DOI:10.11821/xb200610010
[本文引用: 1]

This paper proposes a new method to simulate development plans based on the integration of multi-agent systems (MAS) and cellular automata (CA). The proposed model consists of three related components, i.e., multi-agent systems, cellular automata (CA) and GIS. The mechanism to achieve spatial and temporal efficiency in using land resources is implemented according to the theories of environmental economics and sustainable development. This scheme is helpful for promoting sustainable use of land resources in fast growing regions. The proposed model is applied to the simulation of land use dynamics in the Haizhu district of Guangzhou in 1995-2010. The model is able to simulate various planning scenarios and provide a spatial exploratory tool for planning purposes.
基于多智能体的土地利用模拟与规划模型
Spatial characteristics analysis for multifunctional transition of suburban agricultural areas in Beijing
DOI:10.13249/j.cnki.sgs.2011.04.427
[本文引用: 5]

Because of the different natural conditions, urbanization and industrialization, the circles of suburban agricultural areas in Beijing has different productive / non-productive functions. In this paper, agricultural multifunctionality theory and industrial economy theory have been employed to analyze the spatial characteristics of surburban agriculture area in Beijing. The reslute shows that the agriculture can be divided into two transition pathways from the plain outskirts to the outer mountainous suburbs. Firstly, agricultural transition pathway has emerged from modern urban agriculture to the traditional agriculture; secondly, it is a fan-shaped agricultural transition pathway expanding from the plains to the mountainous area. But there is a non-agricultural industry dominated buffer zone 30–40 km away from the central city, which has become the boundary belt due to urban functions transfering to the village functions. The modern agriculture and recreational agriculture have become the dominant rural economy outside the buffer zone. Its non-productive functions are being strengthened, which are also spreading to the outer mountainous suburb, and the ecological function can be the leading one among the multifunctions in Beijing’s midst and outer spheres.
北京市城郊农业区多功能演变的空间特征
A study on the generalised space of urban-rural integration in Beijing suburbs during the present day
DOI:10.1177/0042098014551675
URL
[本文引用: 4]

Urban–rural integration is a complex process in the giant urban–rural system of the Beijing suburbs with various evolutions in modern suburban functions. Therefore, the functions and processes of the whole Beijing suburb system cannot be treated in isolation. Based on the theory of generalised space proposed by Chen (2008), the urban–rural integration process in the Beijing suburbs was analysed in real space (R-space), phase space (P-space) and order space (O-space). The results show that the macro urban–rural gap is the dominant factor in the O-space. A multifunctional policy at the meso-level will promote the scientific evolution of the P-space. These factors in turn influence the evolution of the urban–rural integration in Beijing suburbs at various levels in the R-space. Finally, new features of spatial organisation, for example, fractals, are generalised from the interactions of those three spaces. Therefore, the perspective of the R-P-O space fusion can provide theoretical guidance to investigators for the urban–rural integration of Beijing suburbs.
Multifractal features of spatial variation in construction land in Beijing (1985-2015)
An analysis of the allometric and multifractal features of a development in the urban-rural area in the lower reaches of the Yangtze River: 2012 cross-sectional data of four provinces and one city
Comparative studies on evolutionary spatial multifractal mechanism for built-up lands in Zhengzhou from 1988 to 2015 with the characteristics of Beijing
Typical and atypical multifractal systems of urban spaces: Using construction land in Zhengzhou from 1988 to 2015 as an example
The corresponding relationships between the demographic transition, urbanization process, and industrial development of China
DOI:10.11821/yj2010120001
[本文引用: 1]

A theory on the corresponding relationships between the industrialization (I), urbanization (U), and demographic transition (D), is presented and the framework is termed as IUD model in this paper. Based on the logistic function, the urbanization curve is divided into four stages: initial state, acceleration stage, deceleration stage, and terminal stage. This presents a striking contrast to R.M. Northam's urbanization curve which was divided into three phases in 1979. The four stages of urbanization remind us of the demographic transition model (DTM) which includes four phases: high stationary phase, early expanding phase, late expanding phase, and low stationary phase. In fact, industrial development can also be divided into four stages: agricultural stage, pre-industrial stage, post-industrial stage, and informational stage. A new principle is advanced as follows. Because of interaction and coupling relationships between industrialization, urbanization, and demographic transition, the four stages of urbanization should coincide with the four stages of industrial structure change, and with the four phases of demographic transition. If not, there are some disharmonious factors in the socio-economic systems, which should be revealed and removed or treated properly. The corresponding theory is then applied to China, and the processes of industrialization, urbanization, and demographic transition are studied by using the statistical data. From 1949 to 2008, China's industrialization and urbanization went from the first stage into the second stage, and are in the second stage now. However, because of the strict policy of family planning, the demographic transition went from the second stage into the third stage. On the whole, the speed of industrialization is faster than that of urbanization to a certain extent, but the speed of demographic transition is much faster than that of both industrialization and urbanization. A conclusion can be drawn as follows. The problem of population ageing will come into being ahead of schedule in comparison with industrialization and urbanization. Twenty years later, the so-called "demographic dividend" will become a "demographic divider", a real population burden for developing industries and cities. The countermeasures and precautions should be researched and taken in advance against the socio-economic syndrome resulting from aging population.
中国人口转变、城市化和产业结构演变的对应关系研究
DOI:10.11821/yj2010120001
[本文引用: 1]

中国的人口转变过程、城市化曲线和产业结构演变都可以划分为四个阶段。在理论上,人口转变、城市化和产业发展的四个阶段大体对应。但是由于计划生育的缘故,我国的人口转变过程提前了,而城市化和工业化都没有跟上步伐,三个发展过程步调不尽一致。目前,中国人口转变处于第三阶段后期,即出生率逐步降低和低死亡率的阶段。但是城市化过程处于第二阶段,即城市化水平快速上升阶段;产业结构演变也处于第二阶段,即第二产业主导的快速工业化阶段。相对于城市过程和产业化过程,中国人口将会提前进入老龄化阶段。这会对我国城乡人口未来的生活造成巨大影响。城市老龄人口的基础设施问题,乡村老年人口的赡养问题等,都需要结合城市化和产业化的具体特征提前考虑应对策略。
Exploring the fractal parameters of urban growth and form with wave-spectrum analysis
Derivation of the functional relations between fractal dimension of and shape indices of urban form
DOI:10.1016/j.compenvurbsys.2011.05.008 URL [本文引用: 3]
Multifractal characterization of urban form and growth: The case of Beijing
DOI:10.1068/b36155 URL [本文引用: 4]
Evolution and mechanism of social-economic space in the rural-urban transition zones
DOI:10.11821/dlxb202112004
[本文引用: 2]

Urban space is characterized by both marketing and planning driven attributes, but very few studies were carried out on the scale of their spatial influence in Chinese academia. This paper takes the rural-urban transition zones of 10 cities in Zhejiang from 1980 to 2010 as the case, aiming to conduct multi-level research which was formed between 60 m to 800 m, including courtyard group level, block level, community level, and residential area level, spatial analysis with the market and planning driving forces. It also analyzes the micro-meso space with the generalized spatial multifractal analysis based on five-year data. Through composition of the spatial regularized, trended and disordered land patches, the analysis shows that there were three basic spatial scales (including market-driven courtyard group level space, plan-driven residential area level space, and the transitional interval of the two-block level space and community level space) in the rural-urban transition zones. The results of spatial expansion analysis show that, due to the different leading roles of market and planning at different scales, the spatial evolution at the courtyard group level, community level, and residential area level was dominated by the combination of trend and regularization, while the spatial evolution at the block level was dominated by the combination of trend and disorder. The results of subjectivity analysis further indicate that under the action of the corresponding driving forces, the courtyard group level space was displayed as agglomeration, while the community level space and the residential area level space were shown as diffusion, and the three have obvious trended characteristics. Furthermore, the development of block level space followed a disordered evolution. The contribution of the paper includes the finding of an objective phenomenon that the spatial pattern of the rural-urban transition zones has often been dominated by tendency and regularity, but the evolution subjectivity is dominated by tendency, due to the combination and its sequence changes of the regularity, trend and disordered on the f(a)-a(q) curve. It will provide a specific scientific basis for the spatial scale division and "the system identification of multi-level features" in territorial spatial planning driving forces.
城乡过渡带社会经济空间演化特征与机理
DOI:10.11821/dlxb202112004
[本文引用: 2]

城市空间具有市场、规划双向驱动的特点,但中国学界对两者空间影响尺度的研究却相对较少。本文以1980—2010年浙江10个城市的城乡过渡带为案例,以其兼有市场、规划驱动的院落组级、街坊级、小区级、居住区级约60 m至约800 m的空间尺度为研究对象,利用5年期数据对这一微中观空间进行了广义空间多重分形分析。整体分析显示,规律化、趋势化和无序化土地斑块演变组分的耦合,在城乡过渡带形成了3个基本尺度区间:市场驱动为主的院落组级空间,规划驱动为主的居住区级空间,两者过渡的街坊级、小区级空间。空间拓展的主导性分析表明,因市场、规划在各尺度上引领作用的不同,院落组级、小区级、居住区级空间演变的趋势化与规律化相复合的特征明显,街坊级则偏于趋势化与无序化复合下的空间演变。主体性分析进一步显示,各尺度区间在相应驱动力的作用下,院落组级空间以趋势化的集聚、小区级、居住区级空间以趋势化的扩散为主;街坊级则突出表现为无序化的空间拓展。本文的贡献在于通过f(a)-a(q)曲线上规律化、趋势化、无序化区间的组合及时序变化,量化地认识了城乡过渡带常为趋势化与规律化相复合的空间拓展所主导、但却以趋势化的空间拓展为主体的客观现象,为国土空间规划中市场、规划的空间影响尺度划分、“多层级特征的系统辨识”提供具体的科学依据。
Multifractal detrended fluctuation analysis of nonstationary time series
DOI:10.1016/S0378-4371(02)01383-3 URL [本文引用: 3]
Fractal geometry for measuring and modeling urban patterns//Albeverio S, Andrey D, Giordano P. The Dynamics of Complex Urban Systems: An Interdisciplinary Approach
A comparison between two OLS-based approaches to estimating urban multifractal parameters
On the spaces and dimensions of geographical systems