EN中文

地理学报, 2023, 78(3): 517-531 doi: 10.11821/dlxb202303001

理论与方法探索

地理分析中的空间效应

刘瑜,1, 汪珂丽1, 邢潇月1, 郭浩1, 张维昱1, 罗琴瑶2, 高松3, 黄舟1, 李海峰2, 李新4, 王姣娥5, 王劲峰5, 朱递6

1.北京大学地球与空间科学学院遥感与地理信息系统研究所，北京 100871

2.中南大学地球科学与信息物理学院，长沙 410083

3.威斯康星大学麦迪逊分校地理系，美国 WI 53703

4.中国科学院青藏高原研究所，北京 100101

5.中国科学院地理科学与资源研究所，北京 100101

6.明尼苏达大学双城分校地理系，美国 MN 55455

On spatial effects in geographical analysis

LIU Yu,1, WANG Keli1, XING Xiaoyue1, GUO Hao1, ZHANG Weiyu1, LUO Qinyao2, GAO Song3, HUANG Zhou1, LI Haifeng2, LI Xin4, WANG Jiaoe5, WANG Jinfeng5, ZHU Di6

1. Institute of Remote Sensing and Geographic Information Systems, School of Earth and Space Sciences, Peking University, Beijing 100871, China

2. School of Geosciences and Info-Physics, Central South University, Changsha 410083, China

3. Department of Geography, University of Wisconsin-Madison, Madison, WI 53703, United States

4. State Key Laboratory of Tibetan Plateau Earth System, Environment and Resources,Institute of Tibetan Plateau Research, CAS, Beijing 100101, China

5. Institute of Geographic Sciences and Natural Resources Research, Chinese Academy of Sciences, Beijing 100101, China

6. Department of Geography, Environment and Society, University of Minnesota, Minneapolis, MN 55455, United States

收稿日期: 2022-10-31   修回日期: 2023-02-24  

基金资助: 国家自然科学基金项目(41830645)
国家自然科学基金项目(41625003)

Received: 2022-10-31   Revised: 2023-02-24  

Fund supported: National Natural Science Foundation of China(41830645)
National Natural Science Foundation of China(41625003)

作者简介 About authors

刘瑜(1971-), 男, 山东人, 教授, 中国地理学会会员(S110007302M), 研究方向为地理信息科学与社会感知。E-mail: liuyu@urban.pku.edu.cn

摘要

地理信息科学传承了地理学的空间分析传统。在地理空间分析中，由于地理空间的特殊性，地理信息科学在构造分析方法时，需要考虑空间效应。然而，空间效应具体的内涵和外延，到目前尚未有系统探讨。本文定义了地理空间效应，进而在形式化定义空间、位置、场、距离、区域等概念的基础上，归纳了4类空间效应：即空间异质性效应、空间依赖的近邻效应、空间交互的距离衰减效应、和空间分区的尺度效应，探讨了4类效应的内在逻辑关系，建立了统一的表达框架。其中，空间异质性效应是最为基础的效应，近邻效应和距离衰减效应反映了地理空间中两个位置之间的二阶关系，尺度效应则由于区域单元的汇总带来，因此这4类效应形成了递进关系。最后本文梳理了目前地理分析中对空间效应的体现，指出了地理空间人工智能技术对于空间效应的揭示和量化能力。

关键词： 地理分析; 空间效应; 空间异质性效应; 近邻效应; 距离衰减效应; 尺度效应; 地理空间人工智能

Abstract

GIScience inherits the spatial analysis tradition of geography. Given that "spatial is special", GIScience needs to highlight spatial effects when constructing methods for geographical analysis. The research presents an explicit definition of spatial effect. By formalizing core GIScience concepts including space, location, field, distance, and region, we identify four types of spatial effects, namely spatial heterogeneity effect, neighbor effect in spatial dependence, distance decay effect in spatial interactions, and scale effect in spatial zoning. A unified framework is constructed to cover the four spatial effects based on the inherent linkages among them. We argue that spatial heterogeneity effect is the most fundamental one. While spatial dependence and spatial interaction are two basic geographical processes that represent the second-order relationships between two locations, neighbor effect and distance decay effect reflect the impacts of space. Scale effect is raised when aggregating attributes using regional units. Hence, the four types of effects form a hierarchical system. From a methodological perspective, this paper summaries related GIScience tools that implement different effects, and emphasizes the value of geospatial artificial intelligence for revealing and quantifying spatial effects.

Keywords： geographical analysis; spatial effect; spatial heterogeneity effect; neighbor effect; distance decay effect; scale effect; geospatial artificial intelligence

PDF (1266KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

刘瑜, 汪珂丽, 邢潇月, 郭浩, 张维昱, 罗琴瑶, 高松, 黄舟, 李海峰, 李新, 王姣娥, 王劲峰, 朱递. 地理分析中的空间效应. 地理学报, 2023, 78(3): 517-531 doi:10.11821/dlxb202303001

LIU Yu, WANG Keli, XING Xiaoyue, GUO Hao, ZHANG Weiyu, LUO Qinyao, GAO Song, HUANG Zhou, LI Haifeng, LI Xin, WANG Jiaoe, WANG Jinfeng, ZHU Di. On spatial effects in geographical analysis. Acta Geographica Sinica, 2023, 78(3): 517-531 doi:10.11821/dlxb202303001

1 引言

“地理学是研究地理要素或者地理综合体空间分布规律、时间演变过程和区域特征的一门学科”[1]。空间分布模式及其规律是地理学的基础性问题，因此，空间分析成为地理学的四大传统（空间分析传统、区域传统、人地关系传统和地球科学传统）之一，即关注地理要素的位置、形态、距离、方向等特性，并从中寻求一般性的规则[2]。空间分析是地理学研究的抓手，并传承到地理信息科学[3]。这主要体现在通过对一般性地理分析方法的构建，刻画地理要素分布模式，揭示驱动因素，模拟现在、反演过去、预测未来，从而支持空间决策。

由于空间在地理分析中的核心地位，如何理解空间以及空间有关的各种效应，是构造并适用空间分析方法的关键基础。Longley等[4]认为由于空间是特殊的（Spatial is Special），这使得地理信息科学成为一个有价值的研究方向。因此，地理学家尤其是地理信息科学家，需要回答如下问题：当在地理分析中提及空间时，其具体含义为何?本文定义的空间效应，是指由于地理空间的基本特性以及要素在空间中不同的位置及衍生的空间配置，而对分析结果产生影响的效应。Goodchild[5]指出如果针对地理对象的某项分析结果，不会因为这些对象位置的重排而产生改变，则该分析不能称为空间分析，因为它没有考虑空间效应。Anselin等[6]对空间效应进行了较早的讨论，他们认为空间效应有两方面的含义，即由Tobler地理学第一定律所刻画的空间关联与距离的关系，以及由于空间单元的大小和形状造成观测变量之间的变化，后者也被概括为可变面积单元问题（Modifiable Areal Unit Problem）[7]；空间效应又可以分为空间依赖（Dependence）和空间异质性（Heterogeneity），前者指空间变量值间存在特定关联关系，后者则是指空间单元内要素分布缺乏一致性（Uniformity）。关于空间依赖和空间异质性之间的逻辑关系存在争议，如Anselin等[6]认为空间异质性是空间依赖的特殊情形，但Goodchild[8]指出与Tobler第一定律所刻画的空间依赖相比，空间异质性更为基础，本文支持后一种观点。

此外，由于空间同时也是哲学、数学、物理学等学科的研究主题，回答“空间是什么”这个问题并不像看起来这么简单。因此，本文通过分析地理空间的特征，探讨地理空间建模的不同视角以及相关基础概念，总结4种空间效应及其对应的地理空间分析方法，并尝试建立一个统一表达框架，从而进一步强化地理研究中的空间传统，并支持相应空间分析方法的构建。尤其是在人工智能技术支持下，如何揭示并量化地理空间效应，更是地理信息科学领域需要探究的前沿议题。

2 地理空间及其特征

2.1 地理空间

在大多数地理应用中，所研究的空间范围是容纳人类活动的地球表层空间或者该空间的一部分，如一个国家或城市，我们称之为地理空间。该定义限定了地理空间的范围和尺度：首先，外太空、月球及其他行星表面等不属于地理空间，而全球尺度是地理空间的上限；其次，地理空间通常要足够大，从而形成一个“容器”，能够观察到发生于其中的人类活动模式或地理现象分布格局。因此，在一些学科（如认知心理学）中研究的空间，如桌面空间，就不属于地理空间的范畴。

值得指出的是，近年来随着信息通讯技术的发展，虚拟地理环境[9]、虚拟空间等概念得到了重视。虚拟空间可以视为真实地理空间在信息世界中的映射，一方面，现实世界中的空间效应会因此在虚拟空间中有所体现，另一方面，虚拟空间中的相互作用和演化过程受距离等要素影响的机理存在差异。因此，我们认为虚拟空间中空间效应依然存在，但是具体体现则不完全等同于真实地理空间。

2.2 空间观和空间模型

哲学层面的空间概念的探讨源远流长，在西方可以追溯到古希腊时代。17世纪牛顿的绝对时空观奠定了经典力学的基础。绝对时空观认为空间永久存在，与其中是否包含物体无关。与之相对的是莱布尼茨的相对时空观，认为空间实际上是物体之间关系的集合，而关系则由它们彼此之间的距离和方向决定。

在地理信息系统实现中，空间是位置的集合。位置通常是基于特定坐标系（如经纬网）定义，进而采用坐标几何体或者对空间的规则划分，表达地理对象（如城市、道路、湖泊）或连续分布的现象（如空气污染浓度），这体现了绝对空间的观点。值得指出的，由于日常人们对于地理空间知识的表达是定性或者半定量的，因此，为了模拟这种方式的知识表达及加工，基于场所的定性空间推理体现了对相对空间的支持[10]。

2.3 地理空间的相关概念

2.3.1 场

对于地理空间分析而言，将空间简单视为一个空的容器，无益于刻画空间效应。爱因斯坦认为不存在脱离场（Field）的“空的空间”[11]。这个观点可以帮助理解地理空间的特性，即任何一个地理空间都不是“空的”，而是充斥了各种自然或人文地理要素，这些要素的空间配置形成有意义的结构，并导致地理空间效应。

为了刻画地理空间及其地理要素，有两个建模的视角，即场的视角和要素（Feature）的视角[5,12 -13]，前者借鉴了物理学概念，用于表达连续分布的地理现象（如降水、土地利用等）；后者则关注离散的地理要素（如湖泊）的分布。Liu等[14]指出，基于以下两个原因，场模型比要素模型更为基础：① 要素是基于特定场以及要素类的本体（Ontology），通过一个概念化过程而实现实例化；② 即使对于地理要素，也可以通过一个对象场的形式加以表达。基于上述考虑，我们将地理要素的表达统一抽象为一个映射：f: X➝G，其定义域X为地理空间中位置x的集合，而值域G为不同地理现象（如降水、土地利用）的取值，其值域可以为标量、向量、甚至复杂对象[15]。

2.3.2 距离

从数学的角度定义，度量空间（Metric Space）是一个集合。该集合中的任意元素之间的度量是可定义的，并且符合以下约束：

① d(x1, x2) ≥ 0，当且仅当x1 = x2，d(x1, x2) = 0；

② d(x1, x2) = d(x2, x1)；

③ d(x1, x3) ≤ d(x1, x2)+d(x2, x3)。

对于地理应用而言，度量空间中的元素x1、x2、x3等为位置，而d(x1, x2)表示了两个点之间的距离，体现了空间的差异性。值得指出的是，尽管GIS建模中通常采用的欧氏空间，是平直的度量空间，但是在一些特殊的分析中，可以对距离进行重定义，得到一个“扭曲的”空间，从而凸现一些特定分布模式和地理过程。如Brockmann等[16]采用有效距离（Effective Distance）的概念，简化了疫情传播的规律。值得指出的是，距离变换后度量空间的3条约束未必严格成立，但是通常拓扑特征会保持。

2.3.3 其他基本概念

至此，我们有了对于地理空间的3点基本特征：① 空间是位置的集合；② 空间不是“空洞”的，而是充满了不同类型的场；③ 空间中任意两个位置的距离是可以度量的。基于上述空间、场以及距离的定义，可以定义区域为空间的一个连通子集。区域在地理研究中扮演了分析单元的角色。区域间存在不同的拓扑关系，可采用九交模型[17]（9-Intersection Model）或者区域链接演算[18]（Region Connection Calculus）定义，而区域之间的包含关系在地理空间分析中得到了更多的重视。基于区域定义，给定一个位置x，其邻域为包括x的一个区域，并且满足区域中任意一点x'，到x的距离d(x, x') ≤ δ，其中δ为给定阈值。基于地理空间场f(x)，给定区域E，可以定义一个汇总函数S({f(x)|x∈E})，从而得到该区域的属性值。其中S是一个对f(x)的汇总函数，包括平均值、众数、极值等。特别的，如果f(x)是一个对象场，则S可以是对对象计数的函数。在实际实现中，平均值和计数是通常的两种汇总途径，前者如平均高程，后者如统计一个区域的病例数目。这区分了两种不同的度量，即空间强度量（Spatially Intensive）和空间广延量（Spatially Extensive）。分辨两种度量的一个简单原则是：当合并两个区域时，空间强度属性要进行平均，而空间广延属性要进行加和。

场模型定义地理要素的空间分布形态，然而，为了进一步发现有意义的空间结构，必须在位置和位置之间建立联系，Goodchild等[19]提出了“地理偶极（Geo-dipole）”的概念，它是一个映射h = g(x1, x2)，其中x1、x2为空间中的两个位置。刘瑜等[20]称之为空间二阶量，与传统一阶量相比，其管理存储空间复杂度更高。距离是基于空间特性定义的一类特殊二阶量。此外，为表征两个位置之间地理环境的相似度，可构造二阶量函数sim(f(x1), f(x2))，其中f(x)表示不同类型的场在位置x的取值。例如，如果研究感兴趣的场有3个：海拔高度（m）、年均温度（℃）、年总降水（mm），两个位置的取值分别为(1000, 15, 1600)和(800, 18, 2100)，则根据预定义的相似度函数sim，可以计算这两个位置地理环境的相似程度。相似度在地理分析中扮演了重要角色，很多操作，如空间区划，其基础就是相似性度量。不论是距离还是相似度，都可以基于空间及预定义的函数进行计算，因此称之为可导出二阶量（Derivable Second-Order Measures），与可导出二阶量不同，观测二阶量（Observed Second-Order Measures）度量了两个位置之间基于物质、信息或人的流动等形成的联系。同样的，给定两个区域R1和R2，可以对其间所有位置形成的地理偶极（或二阶量）进行汇总，从而得到R1和R2之间的二阶量数值，其操作可以形式化表示为S2gx1,x2|x1∈R1,x2∈R2。一个典型的汇总操作是，统计两个区域间的流，得到它们之间的空间交互强度（图1）。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   几种不同形式的空间汇总操作

注：图a对普通场（如DEM）进行汇总（如取平均值），得到空间强度度量；图b对对象场进行汇总（如计数），得到空间广延度量；图c对流进行汇总，得到两个地理单元（A和B）之间的空间交互（其中汇总时考虑了方向性，如果不考虑方向则空间交互强度为7）。

Fig. 1   Several spatial aggregation operations


空间分析不仅涉及对地理要素表象的描述，还关注空间过程的推断，后者有助于揭示地球表层系统的运行机制，具有更重要的科学价值[21]。在地理信息系统中，空间过程指的是描述空间数据产生机制的数学模型，一般表达为映射Φ:U➝v，或概率分布v~P(U)，其中向量U是空间变量v的一组解释变量。模型的样本通常是观测点或空间单元，前者属性值是对空间场的采样，后者属性值则由空间场汇总得到。例如，两个空间变量u和v的线性关系可表达为v=βu或v~N(βu,σ2)，前者表达确定性的规律，后者则引入了服从正态分布的随机误差。

3 地理空间效应

3.1 空间异质性效应

空间异质性（Heterogeneity）与同质性（Homogeneity）相对，具有形态（Form）和过程（Process）两个层面的含义[21-22]。空间形态的异质性描述地理要素空间分布的非均匀性，即空间场f(x)的取值随空间位置变化，若x1 ≠ x2，则较大概率有f(x1) ≠ f(x2)。由于描述地理现象的场取恒定值是一种极端简单情形，因此这一层面的异质性是普遍存在的。但在实际应用中，受观测手段限制或出于人为简化的需要，也会将某个局部区域内的空间场视为同质。王劲峰等[23]进一步区分了空间局部异质性和空间分层异质性，如果子区域统计的方差之和小于区域总方差则存在空间分层异质性。空间过程的异质性指数据在不同空间位置的生成机制存在差异，表现为相应模型的形式或参数随空间位置变化，也称为空间非平稳性（Spatial Non-stationarity），它是环境和社会科学领域建模中的常见现象[24-25]。空间数据的异质性不能推出空间过程的异质性，例如每个位置取值独立同分布的空间随机场，其单次采样的结果（即观测到的空间场）很可能是异质的。地理加权回归系数反映的变量间关系的空间变异即是空间过程异质性的一种表现形式[26]。而在空间随机场的视角下，本文所述的空间过程同质性是严平稳性的一种弱化，前者只要求每个位置点处的随机变量服从相同的分布，后者还要求任一组位置点处的联合分布在平移后保持不变。在方差有限的条件下，地统计学中常用的二阶平稳性是严平稳性的另一种弱化。

空间异质性是地理学存在的学科基础[3,27]，同时也对地理分析带来了挑战。空间非平稳性的存在，意味着像其他自然科学（如物理学）那样，采用全局建模范式（即对研究区域内所有数据点建立单一模型）通常难以适用[28]，因此有“物理学嫉妒”（Physics Envy）的说法[29]。值得注意的是，由于空间过程无法直接观测，只能由可观测的空间数据推断得到，建模得到的非平稳性不一定是真实的，如遗漏变量和函数形式误设都可能导致伪异质性[30]。此外，对描述数据或过程的谓词进行泛化可以将异质转化为同质[3]。给定两个场f1和f2，及空间位置x1和x2，在位置x1有f1(x1) = 3f2(x1)，在位置x2有f1(x2) = 5f2(x2)，则可以将系数视为一个新的空间变量c，从而使得f1和f2之间遵循相同的规律f1(x) = cf2(x)。在此意义上，空间异质性具有相对性。

3.2 空间近邻效应

空间依赖是指由于所研究的变量的性质和空间单元的大小、形状和配置而导致的空间参照数据之间的关系[31]，它描述了广泛观察到的空间数据方差随距离增加的趋势[32]。空间依赖的近邻效应反映了地理现象这样一种情况：给定场f1、f2，在位置x观察到的数值f1(x)，取决于附近满足d(x, x') < δ的近邻位置x'在同一个场中的观察值f1(x')，或者不同场的观察值f2(x')[33]。因此，空间依赖不仅包括不同单元同一变量间的空间依赖，也包括不同空间单元、不同变量间的空间依赖。这种空间关联与位置近邻之间的关系，在Tobler[34]提出的地理学第一定律中得以表达。与空间异质性相似，空间依赖的近邻效应也可以从数据层面延伸到过程层面，即近邻位置具有相似的空间过程[21]。

空间依赖及近邻效应对地理分析意义重大。如果地理现象仅仅存在空间异质性，而没有呈现出空间依赖所定义的规律性，那么将无法发现有意义的空间分布模式，也无法识别有意义的地理要素。例如，地理学家之所以能够建立高原等地貌概念，正是因为在描述地形的场中，相近的区域地形特征相近，从而形成有意义的、空间连通的地貌单元（如山谷）。此外，如果近邻效应不存在，意味着很多空间分析方法（如空间插值）将会无效，这将从根本上动摇地理分析的根基。

Getis[35]认为空间依赖存在距离阈值，在间隔超过距离阈值（如地统计学中的变程）之外的两个位置之间，不存在空间依赖性，即超出阈值之外的两个位置不具有近邻关系。在地理分析中，通常用空间自相关（Spatial Autocorrelation）来衡量不同空间单元间同一变量间的空间依赖[36]。度量和理解空间数据的自相关有助于帮助人们理解空间数据的分布模式[37]，并为基于空间自相关的空间插值提供了理论基础[38]。但是，空间自相关的存在违背了经典统计学中变量独立的假设，因此也可能给空间分析带来困难。例如空间自相关使得经典统计抽样方法应用于空间数据时产生样本方差畸变、有效样本量偏少等问题，也会导致普通最小二乘法在空间回归中产生无效估计或不可靠的统计推论。

3.3 距离衰减效应

在地理空间中，地物之间存在不同强度的联系，并以物质、能量、信息等方式进行移动和交换，这个过程被称为空间交互[39⇓⇓-42]。空间交互作为一类重要的二阶量，蕴含了动态过程，在不同位置间构建联系，形成特定的空间结构，从而为地理时空格局研究提供重要“窗口”[19,43]。

空间交互受到距离衰减效应的控制[44]。一般而言，两个位置空间距离越近，发生交互的可能性越高，这一点同样也符合Tobler第一定律的内涵[38]。距离衰减有微观和宏观两种表现方式[45]。微观上，两个距离较远的位置之间，由于更高的成本以及更多的干预机会，从而发生交互的概率降低。宏观上，个体的交互概率与距离的负相关关系表现为：在其他变量相对稳定的情况下，两个地理实体之间的交互总量随距离增加而变少。随着交通和互联网的快速发展，空间交互成本不断降低，距离似乎越发无足轻重，所以有“距离消亡”（The Death of Distance）[46]的论断。但是最近的研究发现，在手机通信、以及互联网搜索等非空间移动中，距离的影响虽然有所减弱，但依然是交互建模中不可忽略的影响因素[47⇓-49]。值得指出的是，空间交互和空间依赖都体现了距离的影响，但是空间交互具有全局性，对于给定研究区，乃至地理学研究的最大范围——整个地球表面，其间的两个位置都可以存在空间交互，但是空间依赖则是局部的，当超过特定阈值后，可以认为空间依赖不存在。因此，可以分别用长程距离衰减函数（如负幂律函数）和短程距离衰减函数（如负指数函数）来刻画这两种现象。

3.4 尺度效应

地理要素通常遵循一定程度的斑块分布，在空间中呈现出聚集或排斥现象。为了更好地对斑块空间模式进行分析和概括，往往需要将空间划分为特定面状单元，这一操作称为空间分区。在划分的离散空间单元上，通过汇总函数生成的单元属性值（也称空间聚合量）能够概括原始地理空间场的斑块分布模式[50]。基于不同分区大小和形状计算的空间聚合量可能表现出不同的空间模式、空间分布关系或统计相关关系等[51]。由于空间分区的形状可以任意复杂，并且受到人为影响，如历史上经典的Gerrymander选区划分事件，因此研究更多关注分区大小，即尺度效应的影响，并假定分区形状相对简单。任何地理空间分析都建立在特定空间区划定义方式下，理解和模拟尺度效应是准确分析空间模式和地理过程的前提。

尺度效应体现为变量统计指标及多属性相关关系等随尺度变化而变化。相关研究已经表明单变量方差、多变量相关系数及回归参数等统计特征和空间尺度选取密切相关[7,52 -53]，并且空间广延量相对于空间强度量对尺度变化更加敏感[54-55]。虽然部分研究曾试图模拟尺度效应并处理尺度效应带来的问题，如利用半变异函数识别空间自相关的变程[56]，但这类方法仅使用特定尺度下的地理空间数据计算不同距离上的统计量，并没有评估在多个尺度上聚合数据本身后的统计量变化。另有一些方法试图通过最大化聚合空间内部同质性来寻求最佳尺度，但这涉及到方差—协方差矩阵、复杂的统计推导和计算过程，因而没有被广泛推广[50]。因此，当前常用的最佳尺度选择方法仍是通过比较同一数据和方法在不同尺度下的差异来实现。尽管如此，考虑到不同地理现象或过程有着不同的尺度特征，仍需要更多理论与方法来处理尺度效应带来的问题，寻找通用方法模拟尺度效应，并据此解释地理现象或过程背后可能的机理性因素。

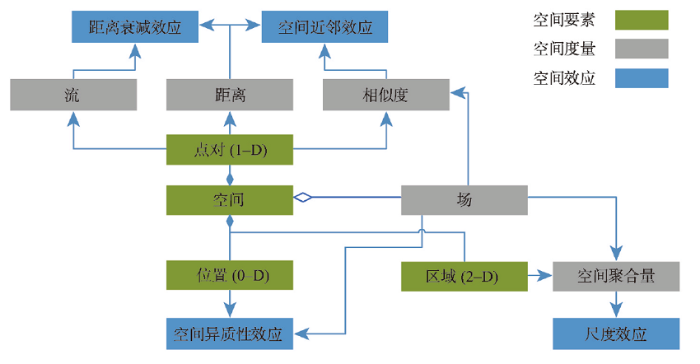
3.5 4种地理空间效应的逻辑关系

4种地理空间效应存在着机理上的逻辑关系。首先，空间异质性是地理现象分布的基本特征，也是理解其他3种空间效应的逻辑基础。对于形态完全同质的空间场，讨论空间依赖没有意义；面状单元的划分方式也不会对分析结果造成影响，从而使得尺度效应消失。空间异质性是空间交互产生的原因之一，当异质性在特定语境下表现为互补性时，则会成为空间交互的促进因素[40]。空间依赖一般随距离增加而减弱，其强度和距离衰减程度也可能随空间位置变化，这可视为空间过程异质性的一种表现形式[6]。

其次，空间依赖的近邻效应和空间交互的距离衰减效应在形式上很相近，但前者表示的是变量的空间配置模式，而后者则表达了动态过程（物质、人、信息等在空间的流动），是形成空间依赖的原因。简单而言，就是相邻位置之间由于空间异质性，形成空间变量的梯度（如温度梯度），进而导致流动和交互（如空气流动），并消弭梯度（空气流动使得在一定范围内温度变得一致），形成空间依赖。在人文地理现象中，该过程同样存在，如Castells等[57]强调的流对于空间结构的影响。在度量空间依赖时，通常假定距离越近，空间依赖就越强，但欧氏距离并不是判断依赖的唯一度量。空间位置距离较远的两个区域之间也可能存在频繁的空间交互，从而增强了区域之间的空间依赖。因此人们可以基于空间交互强度设定距离[15]以度量区域间依赖性。这种距离度量方法近些年来被广泛应用，如在COVID-19空间扩散模拟中[58]。另一方面，地理单元间的位置关系及其属性的空间依赖共同决定了可观察到的空间交互模式[34]。空间交互的强度通常存在空间自相关，空间上邻近的单元倾向于拥有接近的属性值，从而导致邻近空间交互的起点和终点分别具有比较接近的推力和拉力，再加上邻近空间交互的起点到终点的距离衰减也比较接近，因此邻近的空间交互具有接近的空间强度[59]。

第三，几乎所有的地理空间效应都受到尺度的影响。当对空间进行划分并进行地理现象的概括时，总是假定区域内部是均质的。因此，空间依赖程度的度量受到空间聚合尺度及分区方式的影响。尺度越精细，空间单元间呈现空间依赖的概率越大，形状狭长的单元比形状紧凑的单元更容易出现空间依赖[6]。另一方面，变量在最精细尺度上的空间自相关程度影响尺度效应的表现。细粒度上空间自相关的初始水平，决定了变量的方差随着聚集水平增加而改变的速率，使得尺度效应在具有不同初始空间自相关的数据分布上的表现不同[60]。因而在进行多变量分析时，每个变量的空间自相关程度不同将导致很难找到统一的最佳分区[55]。地理大数据由于具有个体粒度信息的观察能力，使得可以从不同尺度研究空间分布模式的变化。例如，针对空间交互，Masucci等[61]从多尺度的空间交互比较了重力模型与辐射模型，结果显示在较大空间尺度的情况下（如国家尺度），辐射模型的效果最优，而在小尺度空间下（如城市尺度），重力模型的表现则更好。

4种地理空间效应之间的内在逻辑关联性，使得构建一个统一的表达框架成为可能。图2表示了构建在一系列基础概念之上的4种效应的关系。其中，空间和场是最为核心的两个概念，其中空间定义了地理研究对象的分布范围，而场则充斥于地理空间，形成了不同地理研究对象的抽象，如地形、气候等。在此基础上，可以通过维度这一几何视角，进一步梳理4种空间效应的概念模型。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   4种空间效应的统一表达框架

Fig. 2   A unified framework for the 4 spatial effects


首先，位置是0维的空间对象，根据场的定义，在每个位置都有特定的表征形态或过程的属性值与之对应，这体现了空间异质性效应。

其次，一维的空间对象定义为两个位置形成的点对，点对是形成空间结构的基础，从而定义不同的地理偶极（或二阶量）。其中，以下3类地理偶极尤为关键：① 点对之间的距离；② 基于两点分别对应的属性值，计算其相似度；③ 两点之间由于不同的流形成的空间交互。相似度和距离的关系体现了近邻效应，而空间交互和距离的关系则表达了距离衰减效应。

第三，在地理空间中，二维空间对象可以定义为区域。为了对地理知识进行概括和归纳，需要根据特定的区域划分结构，对每个区域内部所有位置的场属性进行聚合，得到一个概括的聚合量(如平均高程)，这导致了尺度效应。

综上所述，4类空间效应涵盖了地理空间的0~2维空间对象及其相互关系，这也表明了该分类体系的合理性。

4 空间效应的地理空间分析方法

4.1 传统分析方法

在地理信息科学以及相关领域构造分析方法时，需要充分考虑空间效应，从而体现“空间是特殊的”这一论断。由于地理空间分布同时也是地球科学、生态学、经济学等其它学科的研究对象，因此不同学科对于同一空间效应发展了不同的方法，它们都被吸纳成为地理信息系统的分析工具。下面分别针对四种空间效应进行方法梳理。值得指出的是，空间异质性和空间依赖在实现中往往通过相近的方法（如空间计量模型）体现，因此将其合并介绍。

4.1.1 空间异质性和空间依赖中的近邻效应

空间统计（Spatial Statistics）的发展是为了量化研究区域内的空间聚集程度（Spatial Aggregation）、空间自相关、或空间方差[32]。Moran's I[62]和Geary's C[63]是常见的空间自相关度量指标，可以用来描述全局的空间依赖程度。Anselin在全局空间自相关指标的基础上提出LISA指标，以度量空间数据的局部空间依赖，分析空间数据的局部关联模式[64]。这些局部空间统计的优点之一是可以在每个采样位置映射空间自相关的值，从而识别研究区域内具有正(热点或冷点)或负的(空间异常点)局部自相关的子区域[65]。在地统计（Geostatistics）的空间预测中，待预测位置x0和一个给定的数据点xi越接近，这两个值可能就越相似[32]，预测值z(x0)对数据z(xi)的依赖性可由半变异图（Semi-variogram）估计得到。

空间计量模型也经常被用来研究由空间引起的各种特性[66]，其分析技术旨在纳入地理上相近的位置（或区域）之间的统计相关性[67]。从普通最小二乘模型开始，空间计量经济学研究开发了不同单元之间3种不同类型的空间依赖效应的模型：① 因变量之间的内生相互作用效应（Y与WY），② 解释变量与因变量间的外生相互作用效应（Y与WX），以及③ 误差项之间的交互作用（ε与Wε）。在OLS模型的基础上增加不同的作用项，即发展为不同的空间计量模型。空间计量模型可以对不同单元的同一变量或不同变量之间的空间依赖进行建模，从而更好地解释地理过程，更加精准地预测地理现象。模型中的系数可以表征空间单元间的依赖程度，也可以度量变量间的直接效应和空间溢出效应，前者表示解释变量对本区域因变量的影响，后者则表示解释变量对其他区域因变量的潜在影响[33]，从而将区域间变量的依赖程度分离。

当允许空间计量模型中的参数随空间位置变化时，可以揭示数据背后可能存在的异质空间过程[26,68]，其实现包括空间展开法、地理加权回归、贝叶斯空间变参数模型[69]、基于空间滤波的局部回归[70]等。空间展开法[71]将回归模型中的系数进一步表达为位置坐标的函数。地理加权回归[25]针对同一组变量，采用加权最小二乘法为每个空间单元分别估计回归系数，其中各样本的权重随距离增加而减小。这一方法还可以探测各自变量对因变量作用尺度的差异，已成为应用最为广泛的空间非平稳性探测方法之一[72]。这类基于位置的模型不仅可以表征空间过程的异质性，还体现了空间过程的依赖性。比如在地理加权回归中，模型中各空间单元间的空间权重矩阵表征了空间依赖。这种空间依赖是随距离衰减的，空间单元间的距离越近，赋予的权重值越高；反之，权重值则越低。特征向量空间滤波试图通过去除嵌入的空间依赖性将空间依赖变量转化为独立变量[73]，即将被解释变量的空间自相关效应从解释变量中分离，从而达到校正空间回归模型的目的。特征向量空间滤波方法还可以被推广至空间交互数据，并在人口迁徙流，货物运输流等多种情况下实现了较好的拟合效果[74]。

4.1.2 空间交互的距离衰减效应

空间交互模型主要研究给定两个地理实体间交互强度的数学模型，建立交互强度Tij与起点Oi、终点Dj以及交互成本cij之间的形式化表达。常见的空间交互模型包括重力模型（Gravity Model）[75]、中介机会模型（Intervening Opportunities Model）[76]、最大熵模型（Maximum Entropy Model）[77]和辐射模型（Radiation Model）[78]。在多种模型中，距离被显式或隐式地以交互成本表达在模型中。但是针对不同类型的交互，可以选择多种度量方式确定距离，如欧氏距离、曼哈顿距离、成本距离等，同时距离衰减函数也存在多种方式，如负幂律函数、负指数函数等等。Liu等讨论了多种衰减函数形式的特点及适用场景[45]。空间交互模型中，重力模型由于具有更少的参数和可解释性，被更广泛地接受和拓展。基于起点、终点的流入、流出量约束，可以将重力模型分为单约束、双约束以及无约束模型[79]。Simini等[80]指出重力模型对于起点和终点的属性考虑有限，并且没有纳入地理语境信息，因此设计了Deep Gravity模型，将神经网络与重力模型结合，从而考量更丰富的起讫点属性和地理语境，进一步提高了交互模型的预测能力。

值得指出的是，在空间分析中考察基于一对位置形成的二阶量（包括空间依赖以及空间交互）时，除了它们之间的距离，方向也是一个经常被关注的度量。由于空间异质性的存在，对于给定点x，在不同角度上的位置x'与x形成的度量存在差异，即各向异性（Anisotropy）。因此，在构建空间分析方法时，考虑方向因素可以提高分析效果，如在空间插值中，通过构建各向异性的半变异图，可以构建方向Kriging方法[81]，而Mai等[82]则提出了异性密度的聚类算法以更好识别空间类簇，而在流和空间交互的模式分析中，方向也是度量其自相关特征的重要因素[83]。

4.1.3. 空间分区的尺度效应

寻找合理的分区方案或构造尺度不变的方法指标为处理尺度效应提供了可能。从优化分区角度考虑，空间隐式的分区方法要求区域内部尽可能同质，但不能保证区域连续[84]，需要相对主观的空间连续性处理。空间显式的分区方法则在区域同质性的优化目标基础上，严格地构建了空间连续性约束，例如AZP[85]、ARISeL[86]、REDCAP[87]等。从尺度不变角度来看，在由改进的尺度空间聚类方法定义的不同层级的区域集群上，研究者得到了一致的回归结果，说明该方法可以削弱空间单元尺度选择对分析带来的影响[88]。此外，地理探测器针对空间分异性提出，采用q统计量度量子区域内部方差与全区总方差的差异，在单变量情形下可用于评估分区效果和非线性归因，在多变量情形下可探测解释因素和因变量的广义交叉关系[23]。

4.2 人工智能方法

近年来，以深度学习为代表的人工智能（Artificial Intelligence, AI）技术的快速发展，推动了多个学科的进步，AI for Science正越来越被人们接受。对于地理学而言，空间规律发现、空间过程模拟、以及空间决策优化，可望在大数据以及人工智能支持下自动实现[89-90]。如何将地理空间效应融入AI方法，使其更好地完成空间分析任务，是地理信息科学的核心研究议题之一。特别地，空间数据独有的空间依赖和空间异质性，使得独立同分布假设[91]不再成立，因此Goodchild等[92]提出了弱可重复性（Weak Replicability）的概念来描述人工智能模型在空间效应影响下的泛化性约束。

统计建模得到的对空间依赖性和异质性的估计不一定是准确的，如变量共线性、遗漏变量、函数形式误设等都可能导致对空间效应错误的定量解读[31]。在GeoAI中，对于空间显式（Spatially-Explicit）模块的设计尤为关键[93]，这涉及到考虑空间依赖、距离衰减、空间异质性、尺度等空间效应的更加灵活的模型先验假设。例如，利用卷积生成对抗神经网络可以实现对空间依赖的灵活表达，增强对空间自相关和局部特征的学习，用于实现更精确的空间插值[94]和地统计建模[95-96]。针对空间异质性，可将神经网络与地理加权回归结合，用多层感知机取代地理加权回归中的核函数，以实现回归系数空间变异的精确建模[97]。Spatial-Net框架[98]在学习目标任务（如遥感图像分类）的同时，自适应地将研究区划分为若干子区域，使神经网络模型能够揭示异质的空间过程。利用图卷积神经网络进行空间回归，可以利用部分标注的训练数据实现半监督学习和预测，也可通过引入局部权重顾及空间非平稳性[99]。此外，空间依赖也对模型评价带来了挑战。在空间预测任务中，随机划分训练集、测试集往往使训练样本、测试样本在空间上交错分布；而由于空间自相关的存在，这种划分方式降低了预测的难度，模型的预测精度因此被高估。为消除这一偏差，学界提出了空间留一验证[100]、空间k折交叉验证[101]等方法，在数据集的划分中显式考虑空间依赖的影响。

5 结论

“空间分析”是地理学的四大传统之一，也是构建地理分析方法的关键要素。空间的特殊性是地理信息科学成为一个研究领域的学科基础。然而，空间对于地理分析有哪些影响，目前缺少系统化的梳理。本文在定义一系列地理空间核心概念基础上，归纳了4类地理空间效应，即空间异质性效应、空间依赖的近邻效应、空间交互的距离衰减效应和空间分区的尺度效应，探讨了4类效应的内在逻辑关系，建立了统一的表达框架。在地理信息科学及相关研究领域，如地统计学、空间计量经济学研究中，都实现了相应的分析方法和工具，从而体现不同的空间效应，因此本文对其进行了梳理，以期指导方法的构建。最后，我们指出人工智能方法对地理学带来了全新的机遇，在引入相关方法进行地理分析时，需要充分考虑4类空间效应。

值得指出的是，尽管空间效应源于对于地理现象的分析，但是空间效应的分析方法可不局限于地理空间，如地理探测器q统计被用于细胞分析等[102]。展望未来，随着对地理空间认知的进一步加深，以及地理空间分析方法的进步，地理空间效应的内涵和外延也将随之发展，包括出现新的空间效应，以及不同类型空间效应逻辑关系的演化。

参考文献

Fu Bojie.

Geography: From knowledge, science to decision making support

Acta Geographica Sinica, 2017, 72(11): 1923-1932.

DOI:10.11821/dlxb201711001      [本文引用: 1]

Geography is a subject to explore spatial distribution, time evolution and regional characteristics of geographical elements or geographical complexes. Geography is unique in bridging social sciences and natural sciences, and has characteristics of comprehensiveness, interdisciplinary research and regionalism. With the development of geographical science technology and research methods, geography is in the gorgeous historical process towards geographical science. Research themes of geography are focusing on the comprehensive research on the earth surface. The research paradigms of geography are shifting from geography knowledge description, coupling pattern and process, to the simulation and prediction of complex human and earth system. The development of Chinese geography needs to be rooted in the major needs of national strategy, and plays important roles in the studies of urbanization development, coupling ecological processes and services, water resources management and geopolitics. Under the country's major needs, China's geography tends to achieve the geography theory innovation, new method and technology application and developed disciplinary system with Chinese characteristics, and make more contribution to national and global sustainable development.

[傅伯杰.

地理学: 从知识、科学到决策

地理学报, 2017, 72(11): 1923-1932.]

DOI:10.11821/dlxb201711001      [本文引用: 1]

地理学是研究地理要素或者地理综合体空间分布规律、时间演变过程和区域特征的一门学科,是自然科学与人文科学的交叉,具有综合性、交叉性和区域性的特点。随着地理信息技术发展与研究方法变革,新时期的地理学正在向地理科学进行华丽转身,研究主题更加强调陆地表层系统的综合研究,研究范式经历着从地理学知识描述、格局与过程耦合,向复杂人地系统的模拟和预测转变。在服务国内重大需求和国际全球战略过程中,地理学正在扮演愈发重要的角色,在新型城镇化、生态环境保护、水土资源管理、地缘政治等领域拥有广阔发展前景。中国地理学正面临前所未有的机遇,需要紧紧围绕国家重大需求,创新发展综合性的理论、方法和技术,逐步形成具有鲜明中国特色、深远国际影响的地理科学体系,为中国和全球的可持续发展服务。

Pattison W D.

The four traditions of geography

Journal of Geography, 1964, 63(5): 211-216.

DOI:10.1080/00221346408985265      URL     [本文引用: 1]

Liu Yu, Guo Hao, Li Haifeng, et al.

A note on GeoAI from the perspective of geographical laws

Acta Geodaetica et Cartographica Sinica, 2022, 51(6): 1062-1069.

[本文引用: 3]

[刘瑜, 郭浩, 李海峰, 等.

从地理规律到地理空间人工智能

测绘学报, 2022, 51(6): 1062-1069.]

[本文引用: 3]

Longley P A, Goodchild M F, Maguire D J, et al. Geographic Information Science and Systems. New York: John Wiley & Sons, 2015.

[本文引用: 1]

Goodchild M F.

Geographical data modeling

Computers & Geosciences, 1992, 18(4): 401-408.

DOI:10.1016/0098-3004(92)90069-4      URL     [本文引用: 2]

Anselin L, Getis A.

Spatial statistical analysis and geographic information systems

The Annals of Regional Science, 1992, 26(1): 19-33.

DOI:10.1007/BF01581478      URL     [本文引用: 4]

Fotheringham A S, Wong D W S.

The modifiable areal unit problem in multivariate statistical analysis

Environment and Planning A, 1991, 23(7): 1025-1044.

DOI:10.1068/a231025      URL     [本文引用: 2]

In this paper the examination of the modifiable areal unit problem is extended into multivariate statistical analysis. In an investigation of the parameter estimates from a multiple linear regression model and a multiple logit regression model, conclusions are drawn about the sensitivity of such estimates to variations in scale and zoning systems. The modifiable areal unit problem is shown to be essentially unpredictable in its intensity and effects in multivariate statistical analysis and is therefore a much greater problem than in univariate or bivariate analysis. The results of this analysis are rather depressing in that they provide strong evidence of the unreliability of any multivariate analysis undertaken with data from areal units. Given that such analyses can only be expected to increase with the imminent availability of new census data both in the United Kingdom and in the USA, and the current proliferation of GIS (geographical information system) technology which permits even more access to aggregated data, this paper serves as a topical warning.

Goodchild M F.

The validity and usefulness of laws in geographic information science and geography

Annals of the Association of American Geographers, 2004, 94(2): 300-303.

DOI:10.1111/j.1467-8306.2004.09402008.x      URL     [本文引用: 1]

Lin H, Chen M, Lu G N, et al.

Virtual geographic environments (VGEs): A new generation of geographic analysis tool

Earth-Science Reviews, 2013, 126: 74-84.

DOI:10.1016/j.earscirev.2013.08.001      URL     [本文引用: 1]

Cohn A G, Hazarika S M.

Qualitative spatial representation and reasoning: An overview

Fundamenta Informaticae, 2001, 46(1/2): 1-29.

[本文引用: 1]

Couclelis H.

Space, time, geography

Geographical Information Systems, 1999, 1: 29-38.

[本文引用: 1]

Couclelis H. People manipulate objects (but cultivate fields): Beyond the raster-vector debate in GIS//Frank A U, Campari I, Formentini U. Theories and Methods of Spatio-temporal Reasoning in Geographic Space. Berlin: Springer, 1992: 65-77.

[本文引用: 1]

Bian L.

Object-oriented representation of environmental phenomena: Is everything best represented as an object?

Annals of the Association of American Geographers, 2007, 97(2): 267-281.

DOI:10.1111/j.1467-8306.2007.00535.x      URL     [本文引用: 1]

Liu Y, Goodchild M F, Guo Q, et al.

Towards a General Field model and its order in GIS

International Journal of Geographical Information Science, 2008, 22(6): 623-643.

DOI:10.1080/13658810701587727      URL     [本文引用: 1]

Cova T J, Goodchild M F.

Extending geographical representation to include fields of spatial objects

International Journal of Geographical Information Science, 2002, 16(6): 509-532.

DOI:10.1080/13658810210137040      URL     [本文引用: 2]

Brockmann D, Helbing D.

The hidden geometry of complex, network-driven contagion phenomena

Science, 2013, 342(6164): 1337-1342.

DOI:10.1126/science.1245200      PMID:24337289      [本文引用: 1]

The global spread of epidemics, rumors, opinions, and innovations are complex, network-driven dynamic processes. The combined multiscale nature and intrinsic heterogeneity of the underlying networks make it difficult to develop an intuitive understanding of these processes, to distinguish relevant from peripheral factors, to predict their time course, and to locate their origin. However, we show that complex spatiotemporal patterns can be reduced to surprisingly simple, homogeneous wave propagation patterns, if conventional geographic distance is replaced by a probabilistically motivated effective distance. In the context of global, air-traffic-mediated epidemics, we show that effective distance reliably predicts disease arrival times. Even if epidemiological parameters are unknown, the method can still deliver relative arrival times. The approach can also identify the spatial origin of spreading processes and successfully be applied to data of the worldwide 2009 H1N1 influenza pandemic and 2003 SARS epidemic.

Egenhofer M J, Franzosa R D.

Point-set topological spatial relations

International Journal of Geographical Information Systems, 1991, 5(2): 161-174.

DOI:10.1080/02693799108927841      URL     [本文引用: 1]

Cohn A G, Bennett B, Gooday J, et al.

Qualitative spatial representation and reasoning with the region connection calculus

GeoInformatica, 1997, 1(3): 275-316.

DOI:10.1023/A:1009712514511      URL     [本文引用: 1]

Goodchild M F, Yuan M, Cova T J.

Towards a general theory of geographic representation in GIS

International Journal of Geographical Information Science, 2007, 21(3): 239-260.

DOI:10.1080/13658810600965271      URL     [本文引用: 2]

Liu Yu, Yao Xin, Gong Yongxi, et al.

Analytical methods and applications of spatial interactions in the era of big data

Acta Geographica Sinica, 2020, 75(7): 1523-1538.

DOI:10.11821/dlxb202007014      [本文引用: 1]

Spatial interaction is a critical basis of understanding human processes on the land surface. Together with spatial dependence, it embodies the uniqueness and relatedness of geographical space, as well as the impact on the embedded geographical distribution patterns. Spatial interaction also has distinctive space-time attributes, and thus it is significant to geographical research. Big data bring new opportunities for the studies of spatial interaction, which enables us to sense and observe spatial interaction patterns at different spatial scales, and simulate and predict their dynamic evolution. This provides great support for the research of human activity regularities and regional spatial structures. In this article, we first demonstrated the relationship between spatial interaction and geospatial patterns, and introduced how to sense spatial interaction with big geodata. Then, we generalized the progress of relevant models and analytical methods, and introduced the corresponding applications in fields of spatial planning, urban transportation, public health and tourism. Some key issues were also discussed. We hope this review can provide guidance for the studies of spatial interaction supported by big data.

[刘瑜, 姚欣, 龚咏喜, 等.

大数据时代的空间交互分析方法和应用再论

地理学报, 2020, 75(7): 1523-1538.]

DOI:10.11821/dlxb202007014      [本文引用: 1]

空间交互是理解地表人文过程的重要基础,与空间依赖一起共同体现了地理空间的独特性、关联性以及对嵌入该空间的地理分布格局的影响,具有鲜明的时空属性,因此对于地理学研究具有重要意义。大数据为空间交互研究带来了新的机遇,能够使我们在不同时空尺度感知和观察空间交互模式并对其动态演化特征进行模拟和预测,从而为揭示人类活动规律及区域空间结构提供有力支持。本文在探讨空间交互与地理空间模式关系的基础上,描述了利用地理大数据感知空间交互的方式和定量模型,介绍了空间交互分析方法的研究进展及其在空间规划与交通、公共卫生、旅游等领域的应用情况,并就一些基本问题进行了讨论,以期为大数据支持下空间交互相关研究提供指导。

Goodchild M F.

GIScience, geography, form, and process

Annals of the Association of American Geographers, 2004, 94(4): 709-714.

[本文引用: 3]

Fotheringham A S, Sachdeva M.

Modelling spatial processes in quantitative human geography

Annals of GIS, 2022, 28(1): 5-14.

DOI:10.1080/19475683.2021.1903996      URL     [本文引用: 1]

Wang Jinfeng, Xu Chengdong.

Geodetector: Principle and prospective

Acta Geographica Sinica, 2017, 72(1): 116-134.

DOI:10.11821/dlxb201701010      [本文引用: 2]

Spatial stratified heterogeneity is the spatial expression of natural and socio-economic process, which is an important approach for human to recognize nature since Aristotle. Geodetector is a new statistical method to detect spatial stratified heterogeneity and reveal the driving factors behind it. This method with no linear hypothesis has elegant form and definite physical meaning. Here is the basic idea behind Geodetector: assuming that the study area is divided into several subareas. The study area is characterized by spatial stratified heterogeneity if the sum of the variance of subareas is less than the regional total variance; and if the spatial distribution of the two variables tends to be consistent, there is statistical correlation between them. Q-statistic in Geodetector has already been applied in many fields of natural and social sciences which can be used to measure spatial stratified heterogeneity, detect explanatory factors and analyze the interactive relationship between variables. In this paper, the authors will illustrate the principle of Geodetector and summarize the characteristics and applications in order to facilitate the using of Geodetector and help readers to recognize, mine and utilize spatial stratified heterogeneity.

[王劲峰, 徐成东.

地理探测器: 原理与展望

地理学报, 2017, 72(1): 116-134.]

DOI:10.11821/dlxb201701010      [本文引用: 2]

空间分异是自然和社会经济过程的空间表现,也是自亚里士多德以来人类认识自然的重要途径。地理探测器是探测空间分异性,以及揭示其背后驱动因子的一种新的统计学方法,此方法无线性假设,具有优雅的形式和明确的物理含义。基本思想是：假设研究区分为若干子区域,如果子区域的方差之和小于区域总方差,则存在空间分异性;如果两变量的空间分布趋于一致,则两者存在统计关联性。地理探测器q统计量,可用以度量空间分异性、探测解释因子、分析变量之间交互关系,已经在自然和社会科学多领域应用。本文阐述地理探测器的原理,并对其特点及应用进行了归纳总结,以利于读者方便灵活地使用地理探测器来认识、挖掘和利用空间分异性。

Hagenauer J, Helbich M.

A geographically weighted artificial neural network

International Journal of Geographical Information Science, 2022, 36(2): 215-235.

DOI:10.1080/13658816.2021.1871618      URL     [本文引用: 1]

Chilès J P, Delfiner P. Geostatistics: Modeling Spatial Uncertainty. New Jersey: John Wiley & Sons, 2012.

[本文引用: 2]

Fotheringham A S, Brunsdon C, Charlton M. Geographically Weighted Regression:The Analysis of Spatially Varying Relationships. New York: John Wiley & Sons, 2002.

[本文引用: 2]

Song Changqing.

On paradigms of geographical research

Progress in Geography, 2016, 35(1): 1-3.

DOI:10.18306/dlkxjz.2016.01.001      [本文引用: 1]

Spatial differentiation of natural and human factors in the land surface system of the Earth is the main concern of Geography. Given the complexity of the land surface system, different research methods should be applied to different issues concerning the system. Based on past geographical research, four paradigms were generalized, including geographical empirical paradigm, geographical positivist paradigm, geographical system science paradigm, and geographical big data paradigm. Appropriate paradigms should be employed for different scientific questions, and multiple paradigms should be applied to some complicated questions.

[宋长青.

地理学研究范式的思考

地理科学进展, 2016, 35(1): 1-3.]

DOI:10.18306/dlkxjz.2016.01.001      [本文引用: 1]

地理学主要关注陆地表层自然和人文要素的空间分异规律研究,针对这一复杂系统的不同问题应该选择不同的研究方式。本文在思考以往地理学研究方式的基础上,将地理学研究范式概括为：地理经验科学研究范式、地理实证科学研究范式、地理系统科学研究范式和地理大数据研究范式。对不同地理科学问题应选取不同的范式加以研究,对有些复杂科学问题应采用多种研究范式加以解决。

Fotheringham A S.

Local modeling: One size does not fit all

Journal of Spatial Information Science, 2020(21): 83-87.

[本文引用: 1]

O'Sullivan D, Manson S M.

Do physicists have geography envy?

And what can geographers learn from it? Annals of the Association of American Geographers, 2015, 105(4): 704-722.

[本文引用: 1]

Sachdeva M, Fotheringham A S, Li Z Q, et al.

Are we modelling spatially varying processes or non-linear relationships?

Geographical Analysis, 2022, 54(4): 715-738.

DOI:10.1111/gean.v54.4      URL     [本文引用: 1]

Anselin L, Rey S J. Perspectives on Spatial Data Analysis. Berlin: Springer, 2010.

[本文引用: 2]

Legendre P, Legendre L.

Spatial analysis

Developments in Environmental Modelling, 2012, 24: 785-858.

[本文引用: 3]

LeSage J, Pace R K. Introduction to Spatial Econometrics. Boca Raton: CRC Press, 2009.

[本文引用: 2]

Tobler W R.

A computer movie simulating urban growth in the Detroit region

Economic Geography, 1970, 46(Suppl.): 234-240.

DOI:10.2307/143141      URL     [本文引用: 2]

Getis A. Screening for Spatial Dependence in Regression Analysis. Berlin: Springer, 1990.

[本文引用: 1]

Cliff A D, Ord K.

Spatial autocorrelation: A review of existing and new measures with applications

Economic Geography, 1970, 46(Suppl.): 269-292.

DOI:10.2307/143144      URL     [本文引用: 1]

Cliff A D. Spatial Processes: Models & Applications. London: Pion, 1981.

[本文引用: 1]

Miller H J.

Tobler's first law and spatial analysis

Annals of the Association of American Geographers, 2004, 94(2): 284-289.

DOI:10.1111/j.1467-8306.2004.09402005.x      URL     [本文引用: 2]

Tobler W R.

Spatial interaction patterns

Journal of Environmental Systems, 1976, 6(4): 271-301.

DOI:10.2190/VAKC-3GRF-3XUG-WY4W      URL     [本文引用: 1]

Ullman E L. Geography as Spatial Interaction. Seattle: University of Washington Press, 1980.

[本文引用: 2]

Fotheringham A S, O'Kelly M E. Spatial Interaction Models: Formulations and Applications. Dordrecht: Kluwer Academic Publishers, 1989.

[本文引用: 1]

Roy J R, Thill J C.

Spatial interaction modelling

Papers in Regional Science, 2003, 83(1): 339-361.

DOI:10.1007/s10110-003-0189-4      URL     [本文引用: 1]

Batty M. The New Science of Cities. Cambridge: MIT Press, 2013.

[本文引用: 1]

Wang F H.

Measurement, optimization, and impact of health care accessibility: A methodological review

Annals of the Association of American Geographers, 2012, 102(5): 1104-1112.

PMID:23335813      [本文引用: 1]

Despite spending more than any other nation on medical care per person, the United States ranks behind other industrialized nations in key health performance measures. A main cause is the deep disparities in access to care and health outcomes. Federal programs such as the designations of Medically Underserved Areas/Populations and Health Professional Shortage Areas are designed to boost the number of health professionals serving these areas and to help alleviate the access problem. Their effectiveness relies first and foremost on an accurate measure of accessibility so that resources can be allocated to truly needy areas. Various measures of accessibility need to be integrated into one framework for comparison and evaluation. Optimization methods can be used to improve the distribution and supply of health care providers to maximize service coverage, minimize travel needs of patients, limit the number of facilities, and maximize health or access equality. Inequality in health care access comes at a personal and societal price, evidenced in disparities in health outcomes, including late-stage cancer diagnosis. This review surveys recent literature on the three named issues with emphasis on methodological advancements and implications for public policy.

Liu Y, Wang F H, Kang C G, et al.

Analyzing relatedness by toponym co-occurrences on Web pages

Transactions in GIS, 2014, 18(1): 89-107.

DOI:10.1111/tgis.2014.18.issue-1      URL     [本文引用: 2]

Cairncross F. The Death of Distance:How the Communications Revolution is Changing Our Lives. Cambridge: Harvard Business School Press, 1997.

[本文引用: 1]

Onnela J P, Arbesman S, González M C, et al.

Geographic constraints on social network groups

Plos One, 2011, 6(4): e16939. DOI: 10.1371/journal.pone.0016939.

URL     [本文引用: 1]

Kang C G, Zhang Y, Ma X J, et al.

Inferring properties and revealing geographical impacts of intercity mobile communication network of China using a subnet data set

International Journal of Geographical Information Science, 2013, 27(3): 431-448.

DOI:10.1080/13658816.2012.689838      URL     [本文引用: 1]

Guo H, Zhang W Y, Du H D, et al.

Understanding China's urban system evolution from web search index data

EPJ Data Science, 2022, 11(1): 20.

DOI:10.1140/epjds/s13688-022-00332-y      PMID:35371907      [本文引用: 1]

The spatial inequilibrium phenomenon is apparent during China's rapid urbanization in the past four decades. As the fertility rate decreases and the population ages, this phenomenon will become more critical. To accurately forecast the future economic development of China, it is necessary to quantify the attractiveness of individual cities. This study introduces web search data to quantify the attractiveness of cities with a fine spatial scale (prefecture-level city) and relatively long-term span (nine years). Results confirm that the estimated city attractiveness can unravel a city's capability to attract labor force, and suggest that tourism and health care functions of a city have a positive effect to the city's attractiveness. Additionally, China's north-south gap in economic development has been widened in the past decade, and 11 cities with nationwide influence have prosperous development potential. This study provides a new lens for predicting China's economic development, as well as its spatial patterns.The online version contains supplementary material available at 10.1140/epjds/s13688-022-00332-y.© The Author(s) 2022.

Fotheringham A S, Rogerson P A. The SAGE Handbook of Spatial Analysis. London: Sage, 2008.

[本文引用: 2]

Openshaw S, Taylor P. A million or so correlation coefficients: Three experiments on the modifiable areal unit problem. London: Pion, 1979.

[本文引用: 1]

Clark W A V, Avery K L.

The effects of data aggregation in statistical analysis

Geographical Analysis, 1976, 8(4): 428-438.

DOI:10.1111/gean.1976.8.issue-4      URL     [本文引用: 1]

Wang Y Q, Di Q.

Modifiable areal unit problem and environmental factors of COVID-19 outbreak

Science of the Total Environment, 2020, 740: 139984. DOI: 10.1016/j.scitotenv.2020.139984.

URL     [本文引用: 1]

Gehlke C E, Biehl K.

Certain effects of grouping upon the size of the correlation coefficient in census tract material

Journal of the American Statistical Association, 1934, 29(185A): 169-170.

[本文引用: 1]

Putman S H, Chung S H.

Effects of spatial system design on spatial interaction models. 1: The spatial system definition problem

Environment and Planning A, 1989, 21(1): 27-46.

DOI:10.1068/a210027      URL     [本文引用: 2]

Atkinson P M, Tate N J.

Spatial scale problems and geostatistical solutions: A review

The Professional Geographer, 2000, 52(4): 607-623.

DOI:10.1111/0033-0124.00250      URL     [本文引用: 1]

Castells M, Cardoso G. The Network Society. Oxford: Blackwell, 1996.

[本文引用: 1]

Zhu P Y, Li J R, Hou Y T.

Applying a population flow-based spatial weight matrix in spatial econometric models: Conceptual framework and application to COVID-19 transmission analysis

Annals of the American Association of Geographers, 2022, 112(8): 2266-2286.

DOI:10.1080/24694452.2022.2060791      URL     [本文引用: 1]

Thill J C.

Choice set formation for destination choice modelling

Progress in Human Geography, 1992, 16(3): 361-382.

DOI:10.1177/030913259201600303      URL     [本文引用: 1]

Lee S I, Lee M, Chun Y W, et al.

Uncertainty in the effects of the modifiable areal unit problem under different levels of spatial autocorrelation: A simulation study

International Journal of Geographical Information Science, 2019, 33(6): 1135-1154.

DOI:10.1080/13658816.2018.1542699      URL     [本文引用: 1]

Masucci A P, Serras J, Johansson A, et al.

Gravity versus radiation models: On the importance of scale and heterogeneity in commuting flows

Physical Review E, 2013, 88(2): 022812. DOI: 10.1103/PhysRevE.88.022812.

URL     [本文引用: 1]

Moran P A P.

Notes on continuous stochastic phenomena

Biometrika, 1950, 37(1/2): 17-23.

DOI:10.1093/biomet/37.1-2.17      URL     [本文引用: 1]

Geary R C.

The contiguity ratio and statistical mapping

The Incorporated Statistician, 1954, 5(3): 115-146.

DOI:10.2307/2986645      URL     [本文引用: 1]

Anselin L.

Local indicators of spatial association: LISA

Geographical Analysis, 1995, 27(2): 93-115.

DOI:10.1111/gean.1995.27.issue-2      URL     [本文引用: 1]

Wulder M, Boots B.

Local spatial autocorrelation characteristics of remotely sensed imagery assessed with the Getis statistic

International Journal of Remote Sensing, 1998, 19(11): 2223-2231.

DOI:10.1080/014311698214983      URL     [本文引用: 1]

Anselin L. Spatial Econometrics: Methods and Models. Dordrecht: Kluwer, 1988.

[本文引用: 1]

LeSage J P.

An introduction to spatial econometrics

Revue D Économie Industrielle, 2008, 123(3): 19-44.

[本文引用: 1]

Fotheringham A S, Brunsdon C.

Local forms of spatial analysis

Geographical Analysis, 2000, 31(4): 340-358.

DOI:10.1111/gean.1999.31.issue-4      URL     [本文引用: 1]

Gelfand A E, Kim H J, Sirmans C F, et al.

Spatial modeling with spatially varying coefficient processes

Journal of the American Statistical Association, 2003, 98(462): 387-396.

DOI:10.1198/016214503000170      URL     [本文引用: 1]

Griffith D A.

Spatial-filtering-based contributions to a critique of geographically weighted regression (GWR)

Environment and Planning A, 2008, 40(11): 2751-2769.

DOI:10.1068/a38218      URL     [本文引用: 1]

Casetti E.

Generating models by the expansion method: Applications to geographical research

Geographical Analysis, 1972, 4(1): 81-91.

DOI:10.1111/gean.1972.4.issue-1      URL     [本文引用: 1]

Fotheringham A S, Yang W B, Kang W.

Multiscale geographically weighted regression (MGWR)

Annals of the American Association of Geographers, 2017, 107(6): 1247-1265.

DOI:10.1080/24694452.2017.1352480      URL     [本文引用: 1]

Griffith D A. Spatial Filtering. Spatial Autocorrelation and Spatial Filtering:Gaining Understanding Through Theory and Scientific Visualization. Berlin: Springer, 2003: 91-130.

[本文引用: 1]

Griffith D A, Chun Y W.

Spatial autocorrelation in spatial interactions models: Geographic scale and resolution implications for network resilience and vulnerability

Networks and Spatial Economics, 2015, 15(2): 337-365.

DOI:10.1007/s11067-014-9256-4      URL     [本文引用: 1]

Ravenstein E G.

The laws of migration

Journal of the Statistical Society of London, 1885, 48(2): 167-235.

DOI:10.2307/2979181      URL     [本文引用: 1]

Stouffer S A.

Intervening opportunities: A theory relating mobility and distance

American Sociological Review, 1940, 5(6): 845-867.

DOI:10.2307/2084520      URL     [本文引用: 1]

Wilson A G.

The use of entropy maximising models, in the theory of trip distribution, mode split and route split

Journal of Transport Economics and Policy, 1969, 3(1): 108-126.

[本文引用: 1]

Simini F, González M C, Maritan A, et al.

A universal model for mobility and migration patterns

Nature, 2012, 484(7392): 96-100.

DOI:10.1038/nature10856      [本文引用: 1]

Barbosa H, Barthelemy M, Ghoshal G, et al.

Human mobility: Models and applications

Physics Reports, 2018, 734: 1-74.

DOI:10.1016/j.physrep.2018.01.001      URL     [本文引用: 1]

Simini F, Barlacchi G, Luca M, et al.

A deep gravity model for mobility flows generation

Nature Communications, 2021, 12(1): 6576. DOI: 10.1038/s41467-021-26752-4.

PMID:34772925      [本文引用: 1]

The movements of individuals within and among cities influence critical aspects of our society, such as well-being, the spreading of epidemics, and the quality of the environment. When information about mobility flows is not available for a particular region of interest, we must rely on mathematical models to generate them. In this work, we propose Deep Gravity, an effective model to generate flow probabilities that exploits many features (e.g., land use, road network, transport, food, health facilities) extracted from voluntary geographic data, and uses deep neural networks to discover non-linear relationships between those features and mobility flows. Our experiments, conducted on mobility flows in England, Italy, and New York State, show that Deep Gravity achieves a significant increase in performance, especially in densely populated regions of interest, with respect to the classic gravity model and models that do not use deep neural networks or geographic data. Deep Gravity has good generalization capability, generating realistic flows also for geographic areas for which there is no data availability for training. Finally, we show how flows generated by Deep Gravity may be explained in terms of the geographic features and highlight crucial differences among the three considered countries interpreting the model's prediction with explainable AI techniques.© 2021. The Author(s).

Hansen R O.

Interpretive gridding by anisotropic kriging

Geophysics, 1993, 58(10): 1491-1497.

DOI:10.1190/1.1443363      URL     [本文引用: 1]

Most interpolation algorithms perform poorly on data sampled along profiles crossing features whose length scales are small along the profiles but large transverse to them, such as lineaments. Rather than reproducing the linear features, these algorithms create a series of closures around the profiles. By introducing additional information into the algorithm, in particular by using an anisotropic covariance model for kriging that contains a priori information about the lineations, more realistic results can be obtained. An algorithm of this type produces a much more reasonable map of aeromagnetic data from the Cobb Offset zone of the Juan de Fuca Ridge than either minimum curvature gridding or isotropic kriging.

Mai G C, Janowicz K, Hu Y J, et al.

ADCN: An anisotropic density-based clustering algorithm for discovering spatial point patterns with noise

Transactions in GIS, 2018, 22(1): 348-369.

DOI:10.1111/tgis.2018.22.issue-1      URL     [本文引用: 1]

Liu Y, Tong D Q, Liu X.

Measuring spatial autocorrelation of vectors

Geographical Analysis, 2015, 47(3): 300-319.

DOI:10.1111/gean.12069      URL     [本文引用: 1]

Openshaw S.

A regionalisation program for large data sets

Computer Applications, 1973, 3(4): 136-147.

[本文引用: 1]

Openshaw S.

A geographical solution to scale and aggregation problems in region building, partitioning and spatial modelling

Transactions of the Institute of British Geographers, 1977, 2(4): 459-472.

DOI:10.2307/622300      URL     [本文引用: 1]

Duque J, Church R.

A new heuristic model for designing analytical regions

North American Meeting of the International Regional Science Association, Seattle, 2004.

[本文引用: 1]

Guo D.

Regionalization with dynamically constrained agglomerative clustering and partitioning (REDCAP)

International Journal of Geographical Information Science, 2008, 22(7): 801-823.

DOI:10.1080/13658810701674970      URL     [本文引用: 1]

Mu L, Wang F H.

A scale-space clustering method: Mitigating the effect of scale in the analysis of zone-based data

Annals of the Association of American Geographers, 2008, 98(1): 85-101.

DOI:10.1080/00045600701734224      URL     [本文引用: 1]

Gao Song.

A review of recent researches and reflections on geospatial artificial intelligence

Geomatics and Information Science of Wuhan University, 2020, 45(12): 1865-1874.

[本文引用: 1]

[高松.

地理空间人工智能的近期研究总结与思考

武汉大学学报: 信息科学版, 2020, 45(12): 1865-1874.]

[本文引用: 1]

Ge Y, Ma T, Pei T, et al.

Progress of big geodata

Science Bulletin, 2022, 67(17): 1739-1742.

DOI:10.1016/j.scib.2022.07.022      PMID:36546058      [本文引用: 1]

Atluri G, Karpatne A, Kumar V.

Spatio-temporal data mining: A survey of problems and methods

ACM Computing Surveys (CSUR), 2018, 51(4): 1-41.

[本文引用: 1]

Goodchild M F, Li W W.

Replication across space and time must be weak in the social and environmental sciences

PNAS, 2021, 118(35): e2015759118. DOI: 10.1073/pnas.201575911.

[本文引用: 1]

Janowicz K, Gao S, McKenzie G, et al.

GeoAI: Spatially explicit artificial intelligence techniques for geographic knowledge discovery and beyond

International Journal of Geographical Information Science, 2020, 34(4): 625-636.

DOI:10.1080/13658816.2019.1684500      URL     [本文引用: 1]

Zhu D, Cheng X M, Zhang F, et al.

Spatial interpolation using conditional generative adversarial neural networks

International Journal of Geographical Information Science, 2020, 34(4): 735-758.

DOI:10.1080/13658816.2019.1599122      URL     [本文引用: 1]

Klemmer K, Neill D B. Auxiliary-task learning for geographic data with autoregressive embeddings//Meng X F, Wang F S, Lu C T, et al. Proceedings of the 29th International Conference on Advances in Geographic Information Systems. New York: Association for Computing Machinery, 2021: 141-144.

[本文引用: 1]

Zhang Y F, Yu W H, Zhu D.

Terrain feature-aware deep learning network for digital elevation model superresolution

ISPRS Journal of Photogrammetry and Remote Sensing, 2022, 189: 143-162.

DOI:10.1016/j.isprsjprs.2022.04.028      URL     [本文引用: 1]

Du Z H, Wang Z Y, Wu S S, et al.

Geographically neural network weighted regression for the accurate estimation of spatial non-stationarity

International Journal of Geographical Information Science, 2020, 34(7): 1353-1377.

DOI:10.1080/13658816.2019.1707834      URL     [本文引用: 1]

Xie Y, Jia X, Bao H, et al. Spatial-net:A self-adaptive and model-agnostic deep learning framework for spatially heterogeneous datasets//Meng X F, Wang F S, Lu C T, et al. Proceedings of the 29th International Conference on Advances in Geographic Information Systems. New York: Association for Computing Machinery, 2021: 313-323.

[本文引用: 1]

Zhu D, Liu Y, Yao X, et al.

Spatial regression graph convolutional neural networks: A deep learning paradigm for spatial multivariate distributions

GeoInformatica, 2022, 26(4): 645-676.

DOI:10.1007/s10707-021-00454-x      [本文引用: 1]

Le Rest K, Pinaud D, Monestiez P, et al.

Spatial leave-one-out cross-validation for variable selection in the presence of spatial autocorrelation

Global Ecology and Biogeography, 2014, 23(7): 811-820.

DOI:10.1111/geb.12161      URL     [本文引用: 1]

Pohjankukka J, Pahikkala T, Nevalainen P, et al.

Estimating the prediction performance of spatial models via spatial k-fold cross validation

International Journal of Geographical Information Science, 2017, 31(10): 2001-2019.

DOI:10.1080/13658816.2017.1346255      URL     [本文引用: 1]

Levy-Jurgenson A, Tekpli X, Yakhini Z.

Assessing heterogeneity in spatial data using the HTA index with applications to spatial transcriptomics and imaging

Bioinformatics, 2021, 37(21): 3796-3804.

DOI:10.1093/bioinformatics/btab569      URL     [本文引用: 1]

Tumour heterogeneity is being increasingly recognized as an important characteristic of cancer and as a determinant of prognosis and treatment outcome. Emerging spatial transcriptomics data hold the potential to further our understanding of tumour heterogeneity and its implications. However, existing statistical tools are not sufficiently powerful to capture heterogeneity in the complex setting of spatial molecular biology.

/

〈 〉