EN中文

地理学报 >

2023 , Vol. 78 >Issue 7: 1677 - 1690

DOI: https://doi.org/10.11821/dlxb202307009

水文地理

遥感数据产品率定水文模型的潜力研究

  • 张永强 , 1 ,
  • 黄琦 1, 2 ,
  • 刘昌明 1 ,
  • 杨永辉 3
展开
  • 1.中国科学院地理科学与资源研究所 中国科学院陆地水循环及地表过程院重点实验室，北京 100101
  • 2.中国科学院大学，北京 100049
  • 3.中国科学院遗传与发育生物学研究所农业资源研究中心，石家庄 050022

张永强(1976-), 男, 内蒙古包头人, 研究员, 博士生导师, 主要从事水文学与水资源研究。E-mail:

收稿日期: 2023-05-12

  修回日期: 2023-06-30

  网络出版日期: 2023-08-01

基金资助

国家重点研发计划(2022YFC3002804)

国家自然科学基金项目(41971032)

收起

Potential of using remote sensing product to calibrate hydrological models

  • ZHANG Yongqiang , 1 ,
  • HUANG Qi 1, 2 ,
  • LIU Changming 1 ,
  • YANG Yonghui 3
Expand
  • 1. Institute of Geographic Sciences and Natural Resources Research, CAS, Beijing 100101, China
  • 2. University of Chinese Academy of Sciences, Beijing 100049, China
  • 3. Center for Agricultural Resources Research, Institute of Genetics and Developmental Biology, CAS, Shijiazhuang 050022, China

Received date: 2023-05-12

  Revised date: 2023-06-30

  Online published: 2023-08-01

Supported by

National Key R&D Program of China(2022YFC3002804)

National Natural Science Foundation of China(41971032)

Fold

摘要

地表径流的预测和模拟是水文地理研究的核心，对水资源管理和规划都具有重要意义。传统研究借助于实测地表径流进行水文模型率定和参数移植，对“无测站流域”进行径流预测，但在实测径流稀缺或受到强人类活动（如大坝调控）干扰时，参数移植能力受到限制、预测能力不足。而遥感数据具有时空连续的优势，且不受制于地表径流观测时间序列，为径流预测提供了新思路。本文采用了遥感数据率定水文模型的方法，在中国84个流域探究该方法采用遥感蒸散发、水储量和土壤水数据不同组合率定水文模型，评估各方案预测流域径流的潜力。结果显示基于偏差校正后的网格蒸散发数据约束水文模型的新方法，在中国干旱区和湿润区均具有较大的应用潜力；在格网上约束水文模型相比集总式约束具有较为明显的优越性；应采用多个水文模型提升该方法在不同流域的应用潜力。该方法的径流预测能力具有明显的空间分异性，因地制宜方可有效发挥遥感数据的优势。

关键词： 缺资料地区; 径流预测; PML-V2; 遥感; 蒸散发; 水储量

本文引用格式

张永强 , 黄琦 , 刘昌明 , 杨永辉 . 遥感数据产品率定水文模型的潜力研究[J]. 地理学报, 2023 , 78(7) : 1677 -1690 . DOI: 10.11821/dlxb202307009

Abstract

The prediction and estimation of surface runoff are core research topics in hydrology and geography, with important implications for water resource management and planning. Traditional research relies on measured surface runoff for model calibration and parameter transfer to predict runoff in ungauged basins. However, when measured runoff is scarce or disturbed by strong human activities (such as dam regulation), the ability of parameter transfer is limited, resulting in insufficient runoff prediction capacity. Remote sensing data, with its spatial and temporal continuity, and without being restricted by the observation time series of surface runoff, provides a new approach for runoff prediction. This article explores the method of calibrating hydrological models with remote sensing data in 84 basins in China. Different combinations of remote sensing evapotranspiration, water storage, and soil water data were used to evaluate the potential of predicting runoff by calibrating the hydrological models directly. The results showed that the new method of constraining hydrological models based on grid-based evapotranspiration data with bias correction has great potential for application in both arid and humid areas of China. Grid-based model constraint has a more obvious advantage over lumped model constraint, and multiple hydrological models should be used to enhance the application potential of this method in different basins. The runoff prediction capability and application potential of this method have spatial variability and should be tailored to local conditions to effectively leverage the advantages of remote sensing data.

Key words： ungauged basin; runoff prediction; PML-V2; remote sensing data; evapotranspiration; water storage

1 引言

径流预测对于水资源的开发利用以及洪水灾害风险管理至关重要[1⇓⇓-4]。准确的径流模拟通常需要精确的降水及径流数据，但这对于测站稀缺地区很难实现。尤其是在自然条件恶劣的高寒山区，水文气象测站稀少，仅靠稀缺的地面站点资料很难深度认知该地区水文气象特征。即便在测站相对集中的强人类活动地区，很多水文测站受人类调水影响严重，其观测径流无法表征天然径流过程，因此无法解析天然的降雨—径流关系。
目前，参数区域化方法是无资料或资料稀缺地区径流预测的主流方法，其核心思想是参数移植[5-6]，即将某个测站流域水文模型参数移植到无测站的目标流域。参数区域化方法主要包含3类：基于相似流域的参数移植方法（如属性相似法和空间邻近法等）、基于回归的方法以及基于水文信号的方法[7-8]。Oudin等[9]比较了913个法国流域的经典区域化方案，结果表明，空间邻近法在以上3种区域化方法中能取得更优的效果。而随着空间距离的增加，空间邻近法的表现逐渐变差[10]。因此，在测站严重缺乏地区，空间邻近法可能会受到一定限制。换言之，区域化法在测站稀缺地区（尤其是复杂山区）的应用仍面临巨大挑战。
近年来高精度遥感数据的涌现弥补了观测数据空间不连续的限制，且利用遥感数据直接率定水文模型的方法也得到了一定程度的应用。该方法最大的优点是不受制于实测径流测时间序列的长度和地区，不仅在水文测站稀缺地区具有应用潜力，在强人类扰动的流域也能较好地模拟预测“天然”径流。如Patricia等[11]采用GLEAM实际蒸散发等遥感数据直接约束水文模型，表明单独使用遥感数据约束水文模型在一定程度上合理模拟径流过程；Zhang等[12]采用了基于改进Penman-Monteith-Leuning模型的全球遥感实际蒸散发产品（PML-AET）率定水文模型方法，应用于澳大利亚222个流域，结果表明该方法在湿润地区的月、年尺度径流预测能力较好。研究进一步表明，采用经水量平衡校正后的遥感蒸散发数据约束水文模型，可以获得更高的径流预测精度。如Huang等[13]基于Zhang等的研究，进一步提出了改进型的基于遥感数据率定水文模型方法，通过对遥感数据进行偏差校正的方法获取精度更高的研究区实际蒸散发数据、在0.05°格网上分别率定水文模型，充分发挥了遥感数据空间连续性的优势。近年来，业界对水量平衡闭合订正方面的研究方法已经取得很多进展[14⇓-16]，其中，Budyko水热平衡耦合的假设框架是典型的方法之一，稳健性好[17]。基于Budyko理论的水量平衡订正的蒸散发数据，可以进一步提升基于遥感手段预测天然径流的潜力[13]。中国幅员辽阔，很多流域位于山地和高海拔区域，布设水文测站成本高，遥感数据在这些流域体现出了很大的优势。因此，亟需要探求基于遥感数据率定水文模型的方法在中国不同区域的适用性。
本文研究基于遥感蒸散发率定水文模型的方法在中国若干流域的空间分异特点，进一步挖掘该方法的应用潜力，回答的具体科学问题包括：① 基于遥感手段的天然径流预测潜力在中国不同区域的空间分异特点；② 不同遥感数据率定水文模型方案（格网率定与集总式率定，单一蒸散发数据与多种遥感数据）预测日径流潜力的差异；③ 采用多个水文模型对基于遥感手段的天然径流预测有效性的提升。

2 数据与方法

2.1 研究数据

在遥感及格网产品方面，本文收集了气象格网数据（MSWX[18]、MSWEP[19]）、蒸散发格网数据（PML-V2(China)[20]）、GRACE水储量数据（Liquid Water Equivalent, LWE[21]）以及土壤水数据（SMC[22]）。在水文站点日径流数据方面，本文收集了中国84个水文站点的日径流观测数据。研究数据概况见表1。
表1 研究数据概况

Tab. 1 Overview of the study data

数据名称 全称 空间分辨率 时间分辨率 时间范围 数据链接
MSWEP MSWEP(V2.8)
多源加权融合
降水产品		 0.1° d 1979— http://www.gloh2o.org/mswep/
MSWX 多源气象数据 0.1° d 1979— http://www.gloh2o.org/mswx/
PML-V2(China) 中国区域PML-V2
陆地蒸散发与总初级生产力数据集		 500 m d 2000—2021 https://DOI.org/10.11888/Terre.tpdc.272389
GRACE 重力卫星数据 1° 月 2002—2017 https://developers.google.com/earth-engine/datasets/catalog/NASA_GRACE_MASS_GRIDS_LAND
SMC 中国土壤水数据 0.05° 月 2002—2018 https://DOI.org/10.5281/zenodo.4738556
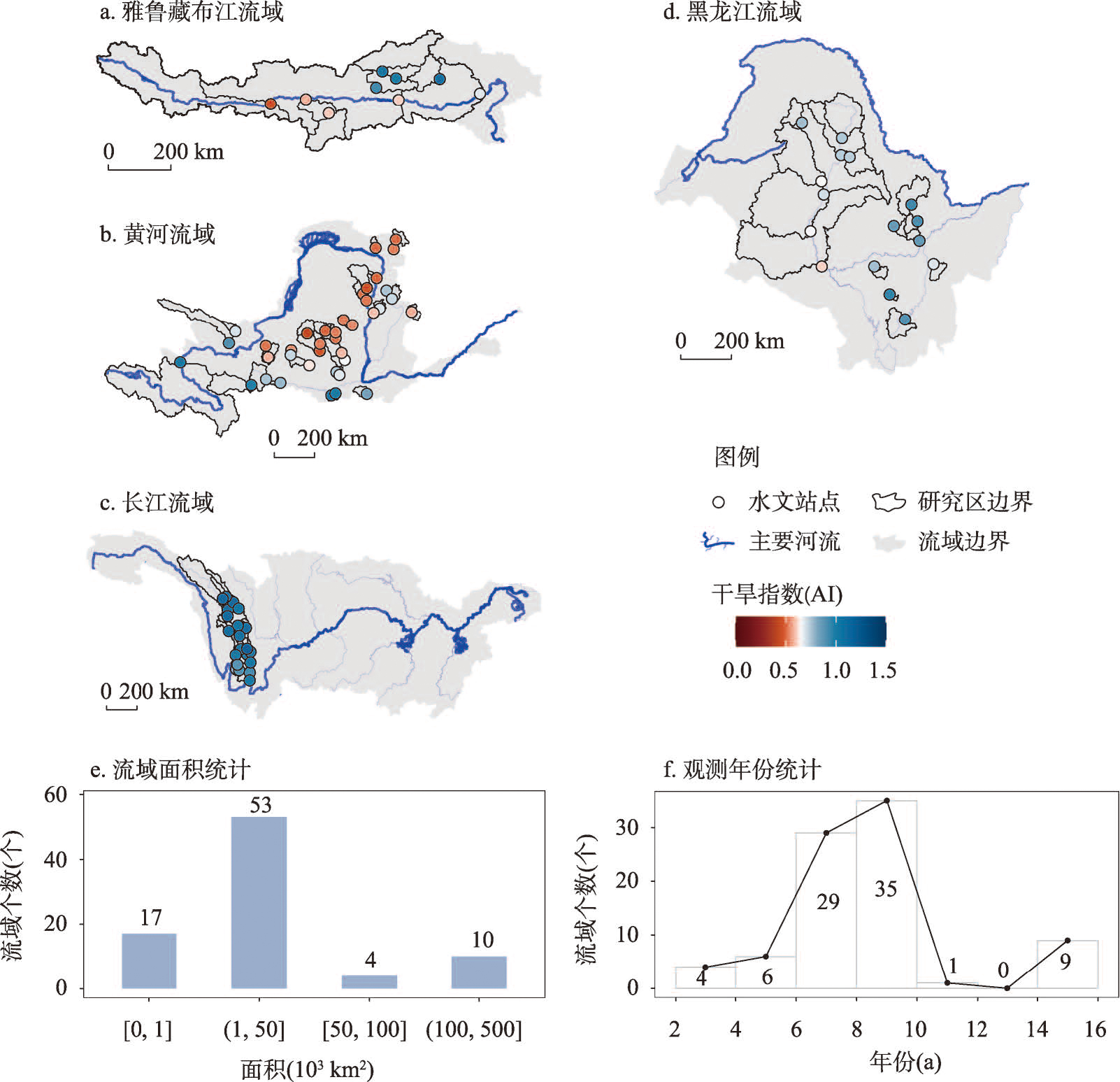
日径流 中国84个水文站日资料 - d 2000—2016
(各站点不同)		 水文年鉴、雅砻江水电开发有限公司
本文气象驱动数据为MSWX，时空分辨率为0.1°、3 h，时间跨度为1979年至今，为水文模型提供了可靠的输入[18]。本文降水驱动来自于MSWEP(V2.8)[19]，融合了全球范围内多种站点资料、遥感及卫星资料以及再分析资料，同时结合径流及潜在蒸散发资料进行订正，是MSWX降水的升级版，与MSWX具有相同的时空分辨率和时间跨度，且广泛应用于中国地区降水评估及水文模拟，在中国大陆地区具有较高精度[23⇓⇓-26]。PML-V2(China)为中国区域陆地蒸散发和总初级生产力数据集[20]，采用PML-V2诊断模型估算了中国区域2000年2月26日—2020年12月31日500 m的日蒸散发数据。该数据包括5个要素：总初级生产（GPP）、植被蒸腾（Ec）、土壤蒸发量（Es）、截留降雨蒸发（Ei）和水体、冰雪蒸发（ET_water）。与PML-V2全球数据[27]相比，PML-V2(China)产品的蒸散发时间分辨率及模拟精度有了一定的提高。本文采用的水储量数据来自重力反演和气候实验数据（Gravity Recovery and Climate Experiment, GRACE）[21]，时间和空间分辨率较粗糙（月尺度、1°×1°、2002年4月—2017年2月）。GRACE数据集分别来自3个机构：喷气推进实验室（Jet Propulsion Laborator, JPL）、德克萨斯大学空间研究中心（University of Texas Center for Space Research, UTCSR）和波茨坦地质勘探局（Geo Forschungs Zentrum Potsdam, GFZ）。本文使用的GRACE数据的水储量数据LWE是3个数据集的平均值。本文采用的土壤水分数据为2002—2018年中国高分辨率土壤水分数据集（A Fine-resolution Soil Moisture Dataset for China, SMC）（0.05°、月尺度）[22]。该数据克服了光学数据源与微波数据源之间的多源数据时间匹配问题，消除了不同传感器观测误差之间的差异。本文采用的径流数据来自中国水文年鉴，根据全球流域属性数据[28]，筛选了径流数据所在时段中84个水库影响小于5%的流域，避免由于人类调水造成模型率定结果不能代表真实产流过程，进而无法验证径流预测能力的问题。
需要指出，不同驱动/遥感数据的时空分辨率不一致（表1）。由于本文将两种月尺度数据（LWE和SMC）作为模型土壤水约束变量，仅需要通过模型输出的土壤水日序列获取月序列，并计算月尺度动态，即可与月尺度遥感土壤水动态数据匹配，无需预处理月遥感数据至日尺度。在空间分辨率的统一上，本文分别将以上数据统一重新分配到0.25°格网和流域集总两种研究尺度。其中，在格网尺度，高分辨率的数据面积加权平均，低分辨率数据（如LWE）以0.25°格网直接提取；在流域集总尺度，这些遥感数据通过面积加权平均的方式平均到流域尺度上。以上数据经过时空尺度的处理后，可以进一步应用于不同方案（见2.3研究方法）、不同模型的输入数据或约束变量。

2.2 研究区概况

本文研究区为中国受人类活动影响小、且满足2000年以来日径流观测数据超过两年的84个流域，研究时段内流域内水库调蓄程度小于5%，水库调蓄程度通过水库库容与多年平均径流量之比来衡量[28]。本文选择的84个流域自北向南覆盖了中国区域的黑龙江流域子流域、黄河流域中上游、长江流域上游及雅鲁藏布江流域（中国境内名称）。研究区大部分为上述四大流域的3级小流域（图1a~1d），流域面积覆盖范围广：其中小于1000 km2的流域有17个，介于1000~50000 km2之间的流域有53个，大于5万km2的流域有14个（图1e）。本文进一步将这些流域划分为1850个0.25°的格网。自2000年以来，流域日径流数据大多为6~10 a（图1f）；干旱指数（多年平均降水与多年平均蒸散发的比值）范围0.44~1.18，其中干旱指数大于0.65为湿润区，小于0.65为干旱区。本文干旱指数采用多年平均MSWEP降水与MSWX计算得出的多年平均潜在蒸散发比值计算，其空间分布与已有研究的中国干旱指数分布图吻合[29]。
图1 研究区概况

Fig. 1 Study area

2.3 研究方法

本文基于直接采用遥感数据率定水文模型的方法，设计了一套模型约束方案，以探索该方法在中国的应用潜力。如图2所示，首先，将遥感气象、潜在蒸散发数据输入到水文模型，即可获得蒸散发、土壤水以及径流等模型输出变量的时间序列。其次，通过采用不同模型约束数据及其对应的约束方程，完成水文模型的率定；最后，统一采用Kling-Gupta效率系数[30]评估各模型约束方案的日径流预测能力。其中，模型率定及检验中使用到的Kling-Gupta效率系数公式如下：
K G E V = 1 - ( c o v ( V o b s , V s i m ) σ o b s 2   σ s i m 2 - 1 ) 2 + ( μ s i m μ o b s - 1 ) 2 - ( σ s i m σ o b s - 1 ) 2
式中： V o b s表示实测变量； V s i m表示模型预测变量；cov表协方差；μ表示平均值；σ表示标准差； K G E V的值从负无穷到1，越接近1表明方案性能越好。
图2 研究技术路线

注：约束方程1表示基准方案：参数区域化法，约束方程中2~5代表遥感手段率定水文模型方案。

Fig. 2 Framework of the study

图2中，遥感蒸散发AET的校正方法见2.3.1，水文模型见2.3.2，约束方案描述见2.3.3。

2.3.1 蒸散发数据校正方法

本文通过傅抱璞公式获取目标流域多年平均蒸散发，并基于此进一步校正目标流域日尺度遥感蒸散发。傅抱璞公式是Budyko框架的衍生，表明了多年平均降水、潜在蒸发以及实际蒸散发的关系[17,31 -32]，该关系以表征流域气候物理特征属性的参数α在傅抱璞公式（公式（2））中体现，而邻近地区的参数α可以认为大致相同。因此，将目标流域多年平均降水、潜在蒸发以及邻近流域参数α作为傅抱璞公式的输入，即可估算目标流域多年平均蒸散发。傅抱璞公式如下所示：
A E T ¯ P - =   1 + E - p P - - ( 1 + ( E - p P   ) α ) 1 / α
式中： P -表示多年平均降水量； E - p为潜在蒸散发； E - p P为潜在蒸散发与多年平均降水的比值，即干燥指数；α为表征流域气候物理特征属性的参数。
本文获取邻近流域的参数α作为目标流域参数α。区别于传统水文模型参数区域化法需要邻近流域大量实测数据的特点，本文采用的参数仅由邻近流域多年平均尺度降水、径流及潜在蒸散发推导，降低了区域化法对邻近流域水文数据的长度及时间分辨率要求。本文在0.25°格网上校正PML-V2(China)蒸散发产品（后简称为PML-V2），校正步骤如下：
第一步：选取某个目标格网的邻近格网（假设目标格网为无资料地区），获取其多年平均降水 P -、多年平均潜在蒸发 E - p以及多年平均径流 Q - o b s。在多年尺度上忽略流域水储量的变化，根据水量平衡原理，令 A E T ¯ = P - -   Q - o b s。
第二步：以 P -、 E - p和 A E T ¯为输入，推导公式（2）中参数 α，获取各目标格网邻近流域的参数α。
第三步：以目标格网 P - '、 E - p '和邻近流域参数 α为输入，在目标格网上应用公式（2），获得目标格网多年平均蒸散发 A E T ¯ '。
第四步：依据目标格网多年平均蒸散发 A E T ¯ '及PML-V2多年平均实际蒸发量，得出PML-V2实际蒸发每个格网的校正因子 S C = A E T ¯ ' / A E T P M L ¯。
第五步：将校正因子SC应用于PML-V2的日数据，可以得到PML-V2的校正后数据。
PML-V2蒸散发的校正在尽可能少采用实测径流时间序列的情况下，完成了格网尺度的校正，通过面积加权平均即可获得流域尺度的校正结果。这对遥感蒸散发率定水文模型方法在径流数据稀缺地区的应用具有重大意义。

2.3.2 水文模型

本文采用了水文研究中具有代表性的3个水文模型：HBV[33-34]、Xinanjiang[35-36]以及SIMHYD[37]水文模型。这3种水文模型均具有蒸散发、土壤水模块，为遥感数据约束对应变量提供了条件，其中HBV模型为加入融雪模块的HBV水文模型。模型结构同Huang等[38]的研究，由于本文侧重于模型率定方案的比较，此处不再详细介绍各水文模型。

2.3.3 参数率定

本文参数优化算法选用了自动优化算法中广泛应用的遗传算法（Genetic Algorithm, GA），由美国的Holland最先于20世纪70年代提出，具有高效、并行、全局搜索的优点[39]。遗传算法通过参数的遗传交叉，在每代搜索过程中通过获取搜索空间相关的信息，并通过迭代交叉优选得出最佳解[39-40]。根据已有采用遗传算法率定Xinanjiang和SIMHYD水文模型的相关研究和前期测试，种群数为400，迭代50次后即可寻到最优解[10]，因此，本文中遗传算法的种群数和进化代数分别取500和50。
为探讨基于遥感数据率定水文模型方法（即实验组）是否具有优势，首先应当设定相对于遥感数据率定水文模型方法的对照组。由于本文中假定研究区为径流数据稀缺地区，故设置对照组为目前径流数据稀缺地区水文模拟的最常用方法——区域化法（基准方案）。本文中采用了区域化法中最邻近法的结果，其参数为各流域最邻近有观测径流数据流域采用径流Q率定水文模型时的该流域参数，区域化法径流预测能力是其他方案的评价基准。模型方案2~5为实验组，主要探索遥感数据率定水文模型方法在中国的空间分异，以及同一类型的要素采用不同数据在该方法表现的空间分异结果。方案2为采用校正的遥感蒸散发约束水文模型方法在0.25°的格网上约束水文模型，并采用面积加权平均法汇总格网径流至流域出口；方案3为采用校正的面平均遥感蒸散发约束水文模型；方案4在方案3的基础上加入GRACE水储量动态数据（LWE）同时约束模型蒸散发和模型土壤水；方案5同方案4，仅在土壤水数据方面不同，采用了中国土壤水数据（SMC）。
理论上，遥感数据率定水文模型方法的率定期时段不受径流数据限制，可以为任意遥感数据覆盖的时段。本文为了保持5种参数率定方案的统一性，其率定时段均采用了流域径流数据覆盖时段。每个流域率定期前两年为模型预热期。

3 结果与分析

3.1 遥感数据率定水文模型方法在中国不同区域的表现

如图3为遥感数据率定水文模型方法的不同约束方案（方案2~5）相对基准方案（方案1）在日尺度径流预测能力KGEQ的散点图。总体上，方案2~5在日尺度与方案1预测径流能力还有一定差距。这种差距在各流域、各约束方案以及各水文模型之间不尽相同。
图3 不同约束方案相对基准方案在日尺度径流评价指标径流预测能力散点图

注：图中<-1的值显示为-1；横坐标为84个流域方案1的径流预测评价结果，第1~4行分别为方案2~5径流预测评价结果；第1~3列分别表示应用HBV、SIMHYD、Xinanjiang 3种水文模型结果。

Fig. 3 Scatters of runoff prediction ability of different schemes against those of baseline scheme

从流域上来看，各方案均在长江流域日径流预测能力最优，黑龙江流域和雅鲁藏布江流域次之，黄河流域最差。在湿润区（如长江流域的雅砻江），在网格上率定XAJ模型（方案2）可以取得和传统区域化法（方案1）接近的模型表现。在干旱区（如黄河流域），网格上率定XAJ模型（方案2）在多数流域可以优于传统区域化法（方案1）的模型表现。在寒冷流域（如黑龙江流域），网格上率定HBV模型（方案2）可以取得和传统区域化法（方案1）接近的模型表现。在高海拔流域（如雅鲁藏布江流域的部分流域），在网格上率定SIMHYD模型（方案2）可以取得和传统区域化法（方案1）接近的模型表现。
图4为格网蒸散发约束（方案2）日尺度Xinanjiang模型的各流域空间分布，图中干旱指数大于0.65的区域为蓝色，干旱指数小于0.65为红色，干旱/湿润程度越大，颜色越深。由图4知，方案2约束Xinanjiang日尺度模型在湿润区预测能力更强，日径流的KGEQ更高。虽然该方法在湿润区具有较高精度，但最邻近法在湿润区已经具有很高精度，因此该方法应用于湿润区集总式水文模型时，未能超越最邻近法结果（图3）。
图4 方案2采用Xinanjiang模型的KGEQ空间分布

Fig. 4 The KGEQ of scheme 2 using Xinanjiang hydrological model

3.2 不同遥感数据率定水文模型方案预测径流能力对比

表2汇总了不同遥感数据率定水文模型方案（方案2~5）的日径流预测能力，其中值来自不同模型、不同流域的集合。从方案之间对比来看，格网ET约束（方案2：0.13±2.01）水文模型提升了流域面平均ET约束（方案3：0.07±2.46）的径流预测能力；总体来看，加入土壤水数据（方案4：-0.01±4.48和方案5：-0.03±3.37）并未进一步提升方案3的径流预测能力。
表2 不同方案日径流预测能力(KGEQ)汇总

Tab. 2 Summary of runoff prediction ability (KGEQ) using different schemes

方案2 方案3 方案4 方案5
最大值 0.80 0.79 0.62 0.78
中值 0.13±2.01 0.07±2.46 -0.01±4.48 -0.03±3.37

注：中值数据为中位数±标准差。

将方案总体结论进一步细分为各流域、各水文模型，可得不同方案日径流预测能力（KGEQ）汇总表（表3）和方案2~5在不同区域、不同模型的日径流预测评价结果（图5）。
表3 不同方案在不同流域应用不同水文模型的日径流预测能力(KGEQ)汇总

Tab. 3 Summary of runoff prediction ability (KGEQ) using different hydrological models in different basins

流域 方案 HBV SIMHYD Xinanjiang
黑龙江流域 方案2 0.29±0.52 0.09±0.53 0.14±0.61
方案3 0.06±0.21 0.29±0.38 0.34±0.55
方案4 -0.03±0.2 -0.05±0.22 0.21±0.9
方案5 0.12±0.26 0.14±0.41 0.19±1.11
雅鲁藏布江流域 方案2 0.19±0.26 0.12±0.19 0.2±0.17
方案3 0.22±0.25 0.12±0.24 -0.05±0.24
方案4 0.13±0.17 0.02±0.3 0.02±0.22
方案5 0.28±0.24 0.01±0.26 0.09±0.19
长江流域 方案2 0.22±0.13 0.42±0.28 0.58±0.14
方案3 0.12±0.23 0.4±0.37 0.48±0.18
方案4 0.08±0.16 0±0.16 0.36±0.21
方案5 0.05±0.19 0.4±0.36 0.37±0.2
黄河流域 方案2 -0.11±1.29 -1.69±3.95 -0.01±1.11
方案3 -0.17±2.02 -2.04±4.66 0.05±1.7
方案4 -0.05±1.16 -0.82±6.15 -0.72±8.95
方案5 -0.16±2.15 -1.7±3.84 -1.17±6.41

注：表中数据为中位数±标准差。

图5 遥感数据约束水文模型方法在不同区域的模型表现

注：红点代表均值，箱体自上而下3条横线分别为75%、50%和25%分位数，竖线两端分别为90%和10%分位数。

Fig. 5 Model performance of remote sensing data based hydrological model calibration at different basins

由表3和图5知，在格网上约束水文模型（方案2）相比集总式约束（方案3）取得更高的径流预测精度。在黑龙江流域，在采用HBV时方案2优于方案3，且方案5在方案3的基础上得到提升，方案4降低了方案3的预测能力；在采用SIMHYD和Xinanjiang模型时方案2、方案4、方案5并未提高方案3的径流预测能力。在雅鲁藏布江流域，采用Xinanjiang模型时，方案2相比方案3径流预测能力得到提高，采用HBV模型时，方案5优于方案3，而采用其他模型、方案，均未进一步提升集总式ET约束水文模型方法的能力。在长江流域，方案2在各水文模型均优于方案3，而方案4、5在方案3的基础上降低了径流预测能力。在黄河流域，虽然方案2采用HBV和SIMHYD时优于方案3，其KGE仍然较低；而方案2采用Xinanjiang时在部分流域相比方案3径流预测能力得到大幅提升，即KGEQ最大值得到提高。同样地，加入土壤水动态数据对方案3径流预测能力提升不大。同样地，结合散点图（图3）来看，在方案3的基础上加入土壤水数据LWE（方案4）或SMC（方案5）约束时，HBV和SIMHYD的径流预测能力在在部分流域相比方案3更优于方案1（例：部分黄河流域方案4与方案5的KGEQ大于0.5，而对应流域方案3的KGEQ小于0.5。这些流域在黄河流域属于个例，因此在表3与图5无法体现），且在结合SMC时具有更高的精度；Xinanjiang在加入LWE和SMC后，大部分流域径流预测能力并未得到明显改进。
综上，方案2在湿润地区（如长江流域、其他流域的部分子流域）预测日径流能力较强，HBV在黑龙江流域和雅鲁藏布江流域加入土壤水动态数据后（方案5）相比方案3进一步提升了径流预测能力。在干旱地区（如黄河流域、雅鲁藏布江的部分流域），方案2即使总体KGEQ不高，仍大幅优于方案3，体现了该方法在干旱区的巨大潜力。

3.3 多水文模型对遥感数据率定方法有效性的提升

根据图3~5和表2~3，汇总得出以下各水文模型在本文研究区应用基于遥感手段预测径流的特征。
Xinanjiang水文模型在湿润区（如长江流域上游）应用方案2时，可以取得较高径流预测精度，其精度和传统区域化法（方案1）接近。且在干旱区（如黄河流域的多数流域）可以优于传统区域化法（方案1）的模型表现。HBV水文模型在高海拔流域（如雅鲁藏布江流域）应用方案2优于其他两种水文模型，在寒冷流域（如黑龙江流域）采用方案2可以取得和传统区域化法（方案1）接近的模型表现。SIMHYD水文模型在高海拔流域（如雅鲁藏布江流域的部分流域）应用方案2~5时，可以取得和方案1相似或更优的径流预测结果。
需要说明的是本文采用的HBV水文模型具有融雪模块，而SIMHYD和Xinanjiang水文模型未嵌入融雪模块，因此在黑龙江流域融积雪较多的地区，在格网上约束后两者时，其径流预测能力相比集总式约束并无显著提升。而在黑龙江流域采用移除融积雪模块后的HBV模型应用方案2后（图6），格网（方案2）结果比集总式（方案3）差，与其他模型一致。因此，在实际应用中，应采用多个水文模型提升该方法在不同流域的应用潜力。
图6 采用移除融积雪模块的HBV模型在黑龙江流域的径流预测评价

注：红点代表均值，箱体自上而下3条横线分别为75%、50%和25%分位数，竖线两端分别为90%和10%分位数。

Fig. 6 The performances of daily runoff using snow-removed HBV model in Amur River

4 结论与展望

本文探索了采用遥感数据直接率定水文模型的方法在中国不同区域预测径流的适用性和潜力。从区域上看，直接采用遥感数据率定水文模型方法在湿润区相比干旱区具有更高的精度，然而该方法在干旱区更有潜力，有可能超越传统的基于实测径流观测序列的最邻近参数移植方法。从模型来看，模型在不同流域的优势各异，应采用多个水文模型提升该方法在不同流域的应用潜力。从约束数据来看，格网蒸散发约束水文模型相比区域蒸散发约束水文模型具有更大优势；采用空间精度更高的土壤水分动态数据（SMC）约束土壤水动态相比采用GRACE水储量动态数据（LWE，空间分辨率较SMC粗糙）提高了部分流域的模型表现；而采用ET结合SMC的方案在黑龙江流域和雅鲁藏布江流域优于仅采用流域平均ET约束的方法。
毋庸置疑，本文还存在一定的不确定性。从数据上来看，即使选择精度较高的输入数据，降雨、径流数据均不可避免地存在一定的偏差，可能对遥感蒸散发的订正带来一定误差；同时，本文采用概念水文模型，水体季节性变化对面平均遥感数据带来的小幅度影响也在本文中没有考虑。在未来研究中，这些可能的误差需要结合实际情况，从多源遥感数据约束的角度进一步分析，如在寒冷地区，可以采用可靠的融积雪遥感数据进一步订正径流过程。从模型上来看，不同的水文模型在不同类型的流域具有一定差异，在实际应用中需要结合多模型进行径流预测，即可在一定程度上提升基于遥感手段的天然径流预测潜力。
尽管存在诸多不确定性，方案2在黄河流域部分流域表现出很大应用潜力，在其他流域，该方案随着空间精度的提升，遥感数据率定水文模型方法也表现出了一定潜力。例如，Patricia等[11]以MSWEP为10 km分布式水文模型输入，以GLEAM实际蒸散发为约束条件在摩洛哥流域率定该水文模型时，取得较高的径流预测能力，优于基于流域属性的区域化法推断的参数预测的日径流。另外，已有研究表明，采用遥感数据约束集总式水文模型在转向半分布式、分布式时，可以取得更高径流预测精度。例如Huang等在雅砻江30个流域上，将该方法应用于格网分布式水文模型时，日径流预测结果优于半分布式和集总式的结果，尤其是优于最邻近法的结果[13]。这一发现表明了采用遥感数据率定水文模型方法的巨大潜力，即当水文模型提高空间分辨率时，遥感数据的空间信息可以得到更有效的利用，获得更精确的径流预测结果。另外，从时间序列的潜力上来看，遥感数据约束水文模型的方法在资料稀缺地区率定水文模型时不会受径流长度的限制，可以为模型率定提供更丰富的信息。
遥感数据率定水文模型方法在中国84个流域预测日径流时具有明显空间分异，且在部分地区优于传统无资料地区径流预测的最邻近参数移植方法。本文对基于遥感手段的天然径流预测潜力在中国的区域分异进行了初步研究，更深入的研究还有待挖掘。另外，本文暂且未考虑其他人类活动可能对径流造成的扰动[41]。考虑到目前遥感数据率定水文模型方法的不足，未来工作将参考已有分布式水文模型在中国的应用[42]，从遥感数据精度改进、模型选择、模型结构的改进以及分布式的遥感数据率定等方面展开，以进一步发挥遥感数据的优势。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
[1]
Hrachowitz M, Savenije H H G, Blöschl G, et al. A decade of predictions in ungauged basins (PUB): A review. Hydrological Sciences Journal, 2013, 58(6): 1198-1255.

DOI

[2]
Montanari A, Young G, Savenije H H G, et al. "Panta Rhei: Everything Flows": Change in hydrology and society: The IAHS scientific decade 2013-2022. Hydrological Sciences Journal, 2013, 58(6): 1256-1275.

DOI

[3]
Sivapalan M, Takeuchi K, Franks S W, et al. IAHS decade on predictions in ungauged basins (PUB), 2003-2012: Shaping an exciting future for the hydrological sciences. Hydrological Sciences Journal, 2003, 48(6): 857-880.

DOI

[4]
Liu Changming, Bai Peng, Wang Zhonggen, et al. Study on prediction of ungauged basins: A case study on the Tibetan Plateau. Journal of Hydraulic Engineering, 2016, 47(3): 272-282.

[ 刘昌明, 白鹏, 王中根, 等. 稀缺资料流域水文计算若干研究: 以青藏高原为例. 水利学报, 2016, 47(3): 272-282. ]

[5]
Liu Suxia, Liu Changming, Zhao Weimin. Towards the methodology for predictions in ungauged basins. Progress in Geography, 2010, 29(11): 1333-1339.

DOI

[ 刘苏峡, 刘昌明, 赵卫民. 无测站流域水文预测(PUB)的研究方法. 地理科学进展, 2010, 29(11): 1333-1339.

DOI

[6]
Yu Ruihong, Zhang Yujin, Zhang Xiaoxin, et al. Review of regionalization methods on streamflow prediction in ungauged basins. Journal of Hydraulic Engineering, 2016, 47(12): 1528-1539.

[ 于瑞宏, 张宇瑾, 张笑欣, 等. 无测站流域径流预测区域化方法研究进展. 水利学报, 2016, 47(12): 1528-1539.]

[7]
Guo Y H, Zhang Y Q, Zhang L, et al. Regionalization of hydrological modeling for predicting streamflow in ungauged catchments: A comprehensive review. Wiley Interdisciplinary Reviews: Water, 2021, 8(1): e1487. DOI: 10.1002/wat2.1487.

DOI

[8]
Li Hongxia, Zhang Xinhua, Zhang Yongqiang, et al. Review of hydrological model parameter regionalization for ungauged catchments. Journal of China Hydrology, 2011, 31(3): 13-17.

[ 李红霞, 张新华, 张永强, 等. 缺资料流域水文模型参数区域化研究进展. 水文, 2011, 31(3): 13-17.]

[9]
Oudin L, Andréassian V, Perrin C, et al. Spatial proximity, physical similarity, regression and ungauged catchments: A comparison of regionalization approaches based on 913 French catchments. Water Resources Research, 2008, 44(3): W03413. DOI: 10.1029/2007WR006240.

DOI

[10]
Li HX, Zhang Y Q. Regionalising rainfall-runoff modelling for predicting daily runoff: Comparing gridded spatial proximity and gridded integrated similarity approaches against their lumped counterparts. Journal of Hydrology, 2017, 550: 279-293.

DOI

[11]
López P, Sutanudjaja E H, Schellekens J, et al. Calibration of a large-scale hydrological model using satellite-based soil moisture and evapotranspiration products. Hydrology and Earth System Sciences, 2017, 21(6): 3125-3144.

DOI

[12]
Zhang Y Q, Chiew F H S, Liu C M, et al. Can remotely sensed actual evapotranspiration facilitate hydrological prediction in ungauged regions without runoff calibration? Water Resources Research, 2020, 56(1): e2019WR026236. DOI: 10.1029/2019WR026236.

DOI

[13]
Huang Q, Qin G H, Zhang Y Q, et al. Using remote sensing data-based hydrological model calibrations for predicting runoff in ungauged or poorly gauged catchments. Water Resources Research, 2020, 56(8): e2020WR028205. DOI: 10.1029/2020WR028205.

DOI

[14]
Feng Y Q, Kuang X X, Liang S H, et al. A simple and efficient method for correction of basin-scale evapotranspiration on the Tibetan Plateau. Remote Sensing, 2021, 13(19): 3958. DOI: 10.3390/rs13193958.

DOI

[15]
Wan Z M, Zhang K, Xue X W, et al. Water balance-based actual evapotranspiration reconstruction from ground and satellite observations over the conterminous United States. Water Resources Research, 2015, 51(8): 6485-6499.

DOI

[16]
Liu W B, Wang L, Zhou J, et al. A worldwide evaluation of basin-scale evapotranspiration estimates against the water balance method. Journal of Hydrology, 2016, 538: 82-95.

DOI

[17]
Budyko M I. Climate and Life. New York: Academic Press, 1974.

[18]
Beck H E, van Dijk A I J M, Larraondo P R, et al. MSWX: Global 3-hourly 0.1° bias-corrected meteorological data including near-real-time updates and forecast ensembles. Bulletin of the American Meteorological Society, 2022, 103(3): E710-E732.

DOI

[19]
Beck H E, Wood E F, Pan M, et al. MSWEP V2 Global 3-hourly 0.1° precipitation: Methodology and quantitative assessment. Bulletin of the American Meteorological Society, 2019, 100(3): 473-500.

DOI

[20]
He S Y, Zhang Y Q, Ma N, et al. A daily and 500 m coupled evapotranspiration and gross primary production product across China during 2000-2020. Earth System Science Data, 2022, 14(12): 5463-5488.

DOI

[21]
Tapley B D, Bettadpur S, Ries J C, et al. GRACE measurements of mass variability in the Earth system. Science, 2004, 305(5683): 503-505.

DOI PMID

[22]
Meng X J, Mao K B, Meng F, et al. A fine-resolution soil moisture dataset for China in 2002-2018. Earth System Science Data, 2021, 13(7): 3239-3261.

DOI

[23]
Wu Yong. Evaluation of MSWEP precipitation data and their utility in hydrological simulation over Yuanjiang River Basin[D]. Kunming: Yunnan University, 2019.

[ 吴勇. MSWEP降水数据在元江流域的精度检验与水文模拟效果评估[D]. 昆明: 云南大学, 2019.]

[24]
Xu Xintong, Zhu Li, Lyu Xiaoyu, et al. Applicability evaluation of MSWEP precipitation product for meteorological drought monitoring in the Yellow River Basin. Arid Land Geography, 2023, 46(3): 371-384.

[ 许昕彤, 朱丽, 吕潇雨, 等. MSWEP降水产品在黄河流域气象干旱监测中的适用性评价. 干旱区地理, 2023, 46(3): 371-384.]

[25]
Deng Yue, Jiang Weiguo, Wang Xiaoya, et al. Accuracy assessment of MSWEP over mainland of China. Advances in Water Science, 2018, 29(4): 455-464.

[ 邓越, 蒋卫国, 王晓雅, 等. MSWEP降水产品在中国大陆区域的精度评估. 水科学进展, 2018, 29(4): 455-464.]

[26]
Huang Qi, Qin Guanghua, Wang Ruimin, et al. Analysis of spatial distribution characteristics of precipitation in Qilian Mountains based on MSWEP. Journal of Hydraulic Engineering, 2020, 51(2): 232-244.

[ 黄琦, 覃光华, 王瑞敏, 等. 基于MSWEP的祁连山地区降水空间分布特性解析. 水利学报, 2020, 51(2): 232-244.]

[27]
Zhang Y Q, Kong D D, Gan R, et al. Coupled estimation of 500 m and 8-day resolution global evapotranspiration and gross primary production in 2002-2017. Remote Sensing of Environment, 2019, 222: 165-182.

DOI

[28]
Linke S, Lehner B, Ouellet Dallaire C, et al. Global hydro-environmental sub-basin and river reach characteristics at high spatial resolution. Scientific Data, 2019, 6(1): 283. DOI: 10.1038/s41597-019-0300-6.

DOI PMID

[29]
Zomer R J, Xu J, Trabucco A. Version 3 of the global aridity index and potential evapotranspiration database. Scientific Data, 2022, 9(1): 409. DOI: 10.1038/s41597-022-01493-1.

DOI PMID

[30]
Gupta H V, Kling H, Yilmaz K K, et al. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. Journal of Hydrology, 2009, 377(1): 80-91.

DOI

[31]
Baw-puh Fuh. On the calculation of the evaporation from land surface. Chinese Journal of Atmospheric Sciences, 1981, 5(1): 23-31.

[ 傅抱璞. 论陆面蒸发的计算. 大气科学, 1981, 5(1): 23-31.]

[32]
Zhang L, Hickel K, Dawes W R, et al. A rational function approach for estimating mean annual evapotranspiration. Water Resources Research, 2004, 40(2): W02502. DOI: 10.1029/2003WR002710.

DOI

[33]
Bergstrom S. The HBV model//Singh V P. Computer Models of Watershed Hydrology. Denver: Water Resources Publications, 1995: 443-476.

[34]
Lindström G, Johansson B, Persson M, et al. Development and test of the distributed HBV-96 hydrological model. Journal of Hydrology, 1997, 201(1): 272-288.

DOI

[35]
Zhao R J. The Xinanjiang model//Singh V P. Computer Models of Watershed Hydrology. Denver: Water Resources Publications, 1995: 215-232.

[36]
Zhao R J. The Xinanjiang model applied in China. Journal of Hydrology, 1992, 135(1): 371-381.

DOI

[37]
Chiew F H S, Peel M C, Western A W. Application and testing of the simple rainfall-runoff model SIMHYD//Singh V P. Computer Models of Watershed Hydrology. Denver: Water Resources Publications, 1995: 335-367.

[38]
Huang Q, Zhang Y, Ma N, et al. Estimating vegetation greening influences on runoff signatures using a Log-Based Weighted Ensemble Method. Water Resources Research, 2022, 58(12): e2022WR032492. DOI: 10.1029/2022WR032492.

DOI

[39]
Holland J H. Genetic algorithms. Scientific American, 1992, 267(1): 66-72.

DOI

[40]
Konak A, Coit D W, Smith A E. Multi-objective optimization using genetic algorithms: A tutorial. Reliability Engineering & System Safety, 2006, 91(9): 992-1007.

DOI

[41]
Liu Jianyu, Zhang Qiang, Chen Xi, et al. Quantitative evaluations of human- and climate-induced impacts on hydrological processes of China. Acta Geographica Sinica, 2016, 71(11): 1875-1885.

DOI

[ 刘剑宇, 张强, 陈喜, 等. 气候变化和人类活动对中国地表水文过程影响定量研究. 地理学报, 2016, 71(11): 1875-1885.]

DOI

[42]
Yang Dawen, Li Chong, Ni Guangheng, et al. Application of a distributed hydrological model to the Yellow River Basin. Acta Geographica Sinica, 2004, 59(1): 143-154.

DOI

[ 杨大文, 李翀, 倪广恒, 等. 分布式水文模型在黄河流域的应用. 地理学报, 2004, 59(1): 143-154.]

Options
文章导航

/

〈 〉