EN中文

Acta Geographica Sinica >

2024 , Vol. 79 >Issue 3: 712 - 731

DOI: https://doi.org/10.11821/dlxb202403010

Territory Resources and Carbon Peak & Neutrality

Spatio-temporal evolution and influencing factors of aggregate carbon intensity of electricity generation in China's cities

  • MA Shiping , 1 ,
  • XIE Yongshun , 2 ,
  • CHEN Hongyang 3, 4 ,
  • ZHANG Wenzhong 3, 4
Expand
  • 1. Institute of Energy, Environment, and Economy, Tsinghua University, Beijing 100084, China
  • 2. School of Environment, Tsinghua University, Beijing 100084, China
  • 3. Institute of Geographic Science and Natural Resources Research, CAS, Beijing 100101, China
  • 4. University of Chinese Academy of Sciences, Beijing 100049, China

Received date: 2023-08-05

  Revised date: 2023-12-18

  Online published: 2024-04-02

Supported by

Strategic Priority Research Program of the Chinese Academy of Sciences(XDA23100302)

National Natural Science Foundation of China(71974109)

National Natural Science Foundation of China(72140005)

Fold

Abstract

The power sector is a critical industry in China's efforts to attain its carbon peaking and carbon neutrality targets. Analyzing the spatio-temporal pattern and influencing factors of the aggregate carbon intensity (ACI) of electricity generation at the city scale is of great significance for refining electricity emission reduction policies and guiding regional collaborative carbon reduction. This study utilizes micro-level data from 21543 power plants with a capacity of 6000 kW or above, in combination with multiple sources of statistical data related to energy, economy, and society, to calculate ACI of electricity generation in China's cities in 2003, 2010, and 2017. Exploratory spatial data analysis, IDA-LMDI decomposition, and STIRPAT modeling are employed to reveal the spatio-temporal patterns and influencing factors. The findings show that: (1) From 2003 to 2017, the ACI of China's electricity generation sector exhibited a notable decline, albeit with a trend of increasing internal differences. Significant spatial differentiation was observed at city scale, with the northeast half of the Bole-Taipei Line maintaining higher levels than the southwest half over an extended period. The degree of spatial agglomeration also increased significantly during this period, with Northeast and North China identified as regions of particular concern in the decline of ACI. (2) The thermal efficiency was the dominant factor in the decline of ACI in the early stage, whereas the electricity generation structure became increasingly influential in the later period. Meanwhile, other power system factors exhibited less influence, though significant spatial differences were observed. (3) The impact of diverse socio-economic determinants on ACI fluctuated over time, engendering modifications in the attributes of the power system through their interactions with the intricate network of power demand, policy, technology, and clean energy expansion opportunities. (4) An inverted U-shaped correlation was observed between ACI and per capita GDP in 2003 and 2010, which transformed into a linear positive association in 2017. This shift can be attributed to the swift emergence of renewable electricity that have challenged the traditional interpretive framework of the Environmental Kuznets Curve hypothesis, which was previously applicable only to thermal power generation. In the future, endeavors aimed at reducing emissions in the electricity sector must comprehensively acknowledge the spatial heterogeneity and sustain attention towards the ramifications of abrupt shifts arising from emerging technologies on the conventional theoretical framework.

Key words： aggregate carbon intensity of electricity generation; city scale; Environmental Kuznets Curve hypothesis; spatio-temporal pattern; influencing factor

Cite this article

MA Shiping , XIE Yongshun , CHEN Hongyang , ZHANG Wenzhong . Spatio-temporal evolution and influencing factors of aggregate carbon intensity of electricity generation in China's cities[J]. Acta Geographica Sinica, 2024 , 79(3) : 712 -731 . DOI: 10.11821/dlxb202403010

1 引言

电力生产是中国碳排放最主要的贡献部门。国际能源署的统计数据表明，2020年中国电力及热力生产碳排放量占全国总排放量的53.38%，该比例比全球水平高10.53%。在碳达峰、碳中和的发展目标下，中国电力部门面临巨大的减排压力[1]。近年来中国电力部门经历了多次技术升级和结构调整，取得了一定的减排成效，展现出极大的减排潜力[2]。在此背景下，开展电力系统碳排放水平及减排效果的时空演变规律及影响因素研究，能够为电力部门实现碳达峰、碳中和及区域协同降碳提供有利参考。
电力生产总碳强度（Aggregate Carbon Intensity, ACI）是衡量电力系统碳排放水平的重要指标之一，即电力生产消耗化石燃料产生的二氧化碳量与所有生产方式的发电总量的比值。该指标综合考虑了多种发电方式，是一种标准化指标，计算方法简单且便于横向和纵向比较[3]。已有学者分别从国家[3]、六大区域电网[4]和省级尺度[5⇓⇓-8]对中国电力生产总碳强度进行了核算。多尺度核算结果均表明，中国电力生产总碳强度具有明显的空间差异，且近年来变化显著。受制于数据精度及可获取性，现有研究只能利用省级能源统计数据开展电力生产总碳强度核算。但在现实之中，同一省（区）内电力生产特征分异明显，例如冀北和冀南地区、蒙东和蒙西地区均表现出较大差异。因此，突破宏观统计数据限制，开展城市及更精细尺度的电力生产总碳强度核算具有重要价值。
基于电力生产总碳强度的核算结果，现有研究一般通过IDA-LMDI分解进一步探索电力生产总碳强度时空演变的影响因素[9]。根据电力部门的技术特征，电力生产总碳强度通常被分解为化石燃料排放因子、化石燃料组合结构因子、火电能耗因子、发电结构因子、地理效应因子等的乘积，从而反映电力系统自身技术特征变化对总碳强度的影响[10]。中国电网级及省级尺度的研究表明，电力生产总碳强度变化的驱动因素存在明显的时空差异和尺度效应[5-6]。虽然电力生产总碳强度的时空差异由电力系统的技术特征直接决定，但从本质上看是由社会经济因素的时空差异导致。现有研究多关注电力系统技术特征变化对总碳强度的影响，缺乏对社会经济影响因素的分析。
尽管目前少有论文对电力生产总碳强度的社会经济影响因素开展研究，但已有大量研究对碳排放总量[11-12]、人均碳排放量[13-14]以及碳排放强度[15⇓-17]的社会经济影响因素进行了分析，具有重要参考价值。相关研究多以STIRPAT模型为理论基础，以人口规模及密度、人均GDP水平、技术水平、城镇化率、投资水平、产业结构等为解释因素[18]。此外，部分研究引入了环境库兹涅茨曲线假说，探讨碳排放相关指标与人均GDP之间是否存在倒“U”型关系，但受研究方法、数据时间范围、研究尺度等多方面条件影响，研究结论并不一致[11⇓⇓-14]。上述影响因素对电力生产总碳强度的作用效果有待验证，电力生产总碳强度与人均GDP的关系也需要进一步检验。
总体而言，既有研究受制于省级宏观统计数据，对中国电力生产总碳强度的刻画过于粗放；局限于对电力部门技术特征的分解研究，忽略了社会经济因素的作用机制。基于此，本文利用6000 kW及以上电厂微观数据等多源数据，对2003年、2010年和2017年中国城市电力生产总碳强度进行核算，将中国电力生产总碳强度的时空演化特征精细至城市尺度；利用IDA-LMDI分解方法、基于STIRPAT模型的空间回归分析等方法，剖析其电力系统因素和社会经济因素；进而凝练其相互作用机制，检验电力生产总碳强度与经济增长之间的倒“U”型关系，以期为电力部门减排及区域协同降碳工作提供借鉴。

2 研究方法及数据来源

2.1 研究区域与数据来源

2.1.1 研究区域

综合研究目标和数据的可获取性，本文以中国360个城市（数据暂未包含西藏和港澳台）为研究区域，以2003年、2010年和2017年为研究年份。

2.1.2 数据来源

本文核心研究数据为中国6000 kW及以上电厂数据，来自对应年份的《电力工业统计资料汇编》。6000 kW是电力行业统计工作中默认的电厂最小装机容量。2003年、2010年和2017年中国6000 kW及以上电厂数量分别为3327座、5691座及12525座，发电量占全国所有发电机组发电总量的比例分别为97.41%，98.04%和97.96%，包括火电、水电、核电、风电、光伏及其他6种发电类型，利用该数据能够有效反映中国电力生产特征。微观电厂数据包含电厂名称、所在省份、电厂装机容量、发电量、火电发电标准煤耗、火电发电耗用化石燃料量等字段信息。其中，原始数据中少数火电厂（分别占2003年、2010年和2017年发电量比重的8.70%、3.77%和6.86%）缺失“发电标准煤耗”和“发电耗用原煤量”数据，对于此类火电厂进行数据插补，以其所在城市其他火电厂的平均“发电标准煤耗”作为其“发电标准煤耗”，乘以发电量及标煤转换系数获得该火电厂“发电耗用原煤量”。
基于插补后的微观电厂数据，分市统计获得各发电类型对应的装机容量、发电量，以及火电发电耗用不同化石燃料量。由于2010年和2017年原始数据中火电发电消耗各种化石燃料量均被折算为原煤量，本文依据对应年份《中国能源统计年鉴》地区能源平衡表中各省火电消耗不同化石燃料的比例，将2010年和2017年基于微观电厂数据统计获得的城市火电发电耗用原煤量分配为不同类型化石燃料消耗量，2003年则按微观电厂实际消耗不同化石能源量直接分市统计。
电力生产总碳强度核算所需的能源缺省数据如表1所示。其中，化石燃料的平均热值及单位热值含碳量数据来自《中国能源统计年鉴》，发电锅炉的平均碳氧化率数据来自生态环境部发布的《企业温室气体排放核算方法与报告指南——发电设施》。本文所需的社会经济统计数据来自对应年份的《中国城市统计年鉴》、各省市统计年鉴、统计公报、人口普查公报和R&D普查公报等。缺失数据通过插值法补齐，所有经济指标均换算为2003年固定价格。
表1 电力生产总碳强度核算相关缺省数据

Tab. 1 Default data related to aggregate carbon intensity calculation of electricity generation

原煤
 石油 天然气
平均热值(kJ/kg, kJ/m3) 20908 41816 35585
单位热值含碳量(tC/TJ) 26.37 20.08 15.32
发电锅炉平均碳氧化率(%) 99.00 98.00 99.00
标煤转换系数(kg ce/kg, kg ce/m3) 0.71 1.43 1.22

2.2 研究方法

2.2.1 城市电力生产总碳强度核算

根据电力生产总碳强度的定义，其计算公式如下：
V j = C j Q j
式中：Vj表示城市j的电力生产总碳强度；Cj是城市j电力生产产生的二氧化碳总量；Qj表示城市j的发电总量（包括火电、水电、风电、光伏和核电及其他发电方式）。其中，Cj核算仅考虑电力生产的直接排放，即火电生产消耗化石燃料产生的排放，不考虑各种发电方式生产过程中的间接排放，Cj采用基于化石燃料表观消费量的碳排放核算方法①(①政府间气候变化专门委员会（IPCC）的指导方法。)进行计算，具体计算公式如下：
C j = ∑ i C i j = ∑ i F i j × A C V i × C C i × O i ÷ 12 44
式中：Cij是城市j利用化石燃料i发电产生的碳排放量；Fij是城市j火电生产消耗的化石燃料i的量，在本文中仅考虑原煤、石油和天然气3种化石燃料；ACVi是化石燃料i的平均热值；CCi是化石燃料i的单位热值含碳量；Oi是化石燃料i发电主要设备的平均碳氧化率； 12 44是碳与二氧化碳分子量的比值。

2.2.2 泰尔指数

本文利用泰尔指数反应城市间、六大区域电网间和区域电网内的电力生产总碳强度空间差异，具体公式如下：
T a = 1 n ∑ j = 1 n V j V - l n V j V -
T a = T b + T w = ∑ k = 1 6 Y k l n Y k n k / n + ∑ k = 1 6 Y k T k
T k = ∑ m ∈ G k Y m Y k l n Y m / Y k 1 / n k
Y k = ∑ m ∈ G k V m / ∑ j = 1 n V j    
Y m = V m / ∑ j = 1 n V j
D b = T b T a
D w = Y k × T w T a
式中：Ta、Tb、Tw及Tk分别表示总体、区域电网间、区域电网内及第k个区域电网内泰尔指数，数值越大代表电力生产总碳强度的差异越大；n表示研究范围内的城市总数；表示所有城市电力生产总碳强度的平均值；nk表示第k个区域电网Gk包含的城市数量；Yk表示第k个区域电网内城市电力生产总碳强度占所有城市的份额；Ym表示城市m的电力生产总碳强度占所有城市的份额；Vm表示区域电网Gk内城市m的电力生产总碳强度；Db和Dw分别表示各区域电网的组间及组内贡献率。

2.2.3 IDA-LMDI分解

本文采用IDA-LMDI分解方法探究影响电力生产总碳强度的电力系统因素。将全国电力生产总碳强度分解为化石燃料排放因子、化石燃料组合因子、火电能耗因子、发电结构因子和地理效应因子，分别反映化石燃料的碳排放强度、火电部门不同化石燃料的替代情况、火电部门的技术水平、电力生产的清洁化程度和电力生产的空间分布。具体分解公式如下：
V = C Q = ∑ i ∑ j C i j F i j × F i j F j × F j K j × K j Q j × Q j Q = ∑ i ∑ j e i j × q i j × f j × p j × g j
式中：V表示全国电力生产总碳强度；C表示全国电力生产的碳排放总量，由Cij加总获得；Fj表示城市j发电消耗的所有类型化石燃料总量，由Fij折算标煤量后加总获得；Kj表示城市j火电发电量；Qj表示城市j所有类型机组的发电总量；Q表示全国所有类型机组的发电总量，由Qj加总获得；eij为化石燃料排放因子；qij为化石燃料组合因子；fj为火电能耗因子；pj为发电结构因子；gj为地理效应因子。
根据加法分解方法[9]，全国电力生产总碳强度从第t'年到第t年变化ΔV可以被分解为：
Δ V = V t - V t ' = Δ V e + Δ V q + Δ V f + Δ V p + Δ V g
式中：ΔVe、ΔVq、ΔVf、ΔVp和ΔVg分别代表因子eij、qij、fj、pj和gj从第t'年到第t年对全国电力生产总碳强度变动的影响效应。
由式（1）可知，eij由化石燃料i的平均热值、单位热值含碳量和燃烧设备的平均碳氧化率决定，因此eij不随时间和地区发生变化，即∆Ve = 0。其他因子效应的计算方法为：
Δ V q = ∑ i ∑ j V i j t - V i j t ' l n V i j t - l n V i j t ' × l n q i j t q i j t '
Δ V f = ∑ i ∑ j V i j t - V i j t ' l n V i j t - l n V i j t ' × l n f j t f j t '
Δ V p = ∑ i ∑ j V i j t - V i j t ' l n V i j t - l n V i j t ' × l n p j t p j t '
Δ V g = ∑ i ∑ j V i j t - V i j t ' l n V i j t - l n V i j t ' × l n g j t g j t '
本文对2003—2010年、2010—2017年两个时间段内电力生产总碳强度变化的驱动因素进行IDA-LMDI分解分析。IDA-LMDI分解原理要求研究区域在2003年、2010年和2017年3个截面年份的电力生产总碳强度均大于0，因此共280个符合要求的城市进入分解模型。参考既有研究[19-20]，使用极小值（δ = 10-50）对原始数据的零值进行替换。

2.2.4 基于STIRPAT模型的空间回归分析

STIRPAT模型是分析社会经济因素与环境问题之间关系的经典模型[21]，由IPAT模型[22]发展而来，其标准形式为：
I = a × P b × A c × T d × e
式中：I、P、A、T分别表示环境效应、人口、富裕度和科技水平，可根据研究需要扩展；a为模型系数；b、c、d为影响指数；e为误差项。本文以电力生产总碳强度（V）代表环境效应作为被解释变量。在解释变量选择上，参考既有研究，以人口密度（PD）和城镇化率（UR）代表人口因素[11,14,16]，以人均研究与试验发展经费投入（RDP）代表科技水平因素[14]，以人均固定资产投资额（INV）和人均工业增加值（INDP）指标代表富裕度水平，亦能反映产业结构的影响效果[16,23]。考虑到加入人均GDP指标将引发严重的共线性问题，没有将该指标纳入模型之中。将上述变量代入式（16），并对等式两侧分别取对数，可得：
l n V = l n α + β 1 l n P D + β 2 l n U R + β 3 l n R D P + β 4 l n I N V + β 5 l n I N D P + ε
式中：β1, β2, …, β5为解释变量弹性系数，表示对应解释变量每变化1%时，将引起V的β1%, β2%, …, β5%的变化；ε为随机误差项。
为检验电力生产总碳强度与人均GDP之间的关系是否符合环境库兹涅茨曲线，构建如式（18）所示的模型：
l n V = l n α + γ 1 l n G D P P + γ 2 l n G D P P 2 + ε
式中：GDPP代表人均GDP；γ1和γ2为解释变量弹性系数；ε为随机误差项。若γ2 < 0，则说明电力生产总碳强度与人均GDP之间存在倒“U”型曲线关系，即符合环境库兹涅茨曲线假说。
考虑到碳排放可能存在空间集聚效应和空间溢出效应[14,23]，使传统OLS回归方法的估计结果存在一定偏误，因此本文引入空间回归方法进行估计。采用极大似然法分别估计空间滞后方法（SLM）和空间误差方法（SEM），通过似然比检验（LR test）和拉格朗日检验（LM test）判断空间回归方法的有效性。根据数据的可获取性，共325个符合要求的城市进入回归模型。

3 中国电力生产总碳强度的时空演变与集聚特征

3.1 整体发展趋势

基于城市电力生产总碳强度核算结果，分别计算中国及六大区域电网的发电量、电力生产碳排放量及电力生产总碳强度（图1）。就中国整体而言，2003—2017年电力生产总碳强度呈现加速下降趋势，由920.33 gCO2/kWh降至636.90 gCO2/kWh，2003—2010年的年均降幅为1.85%，2010—2017年的年均降幅提升至3.34%。研究期内全国发电总量增加了2.46倍，而电力生产造成的碳排放总量仅增加了1.40倍，表明电力部门减排效果显著。对比既有研究[5,24⇓ -26]的中国电力生产碳排放总量核算结果（图2），本文核算结果的变化趋势与既有研究类似，数值在既有研究估计结果区间范围内，结果可信度较高。
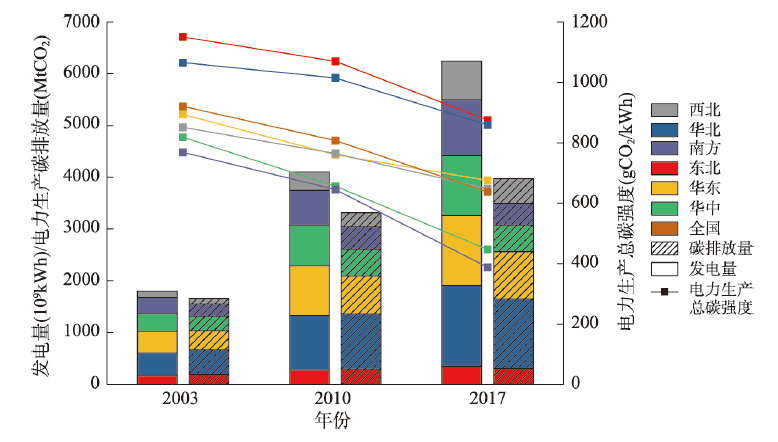
图1 2003—2017年中国及六大区域电网碳排放量、发电量、电力生产总碳强度变化

Fig. 1 The change in CO2 emissions, electricity generation, and ACI of China and six regional power grids, 2003-2017

图2 不同研究中中国电力生产碳排放总量核算结果对比

Fig. 2 Comparison of CO2 emissions in China's electricity generation from different research works

就六大区域而言：① 南方电网和华中电网的电力生产总碳强度最低，在研究期内始终低于全国平均水平。其中，南方电网不仅电力生产总碳强度最低，而且下降幅度最大，研究期内降幅达到380.96 gCO2/kWh；华中电网次之，降幅为370.93 gCO2/kWh。② 东北电网和华北电网的电力生产总碳强度明显高于其他区域，2003年两者均超过1000 gCO2/kWh，2017年仍超过850 gCO2/kWh。但由于电力生产规模的不同，二者对碳排放的贡献有显著差距。华北电网始终是发电规模最大、碳排放量最高的区域电网，2017年电力生产碳排放量占到全国的33.78%；而东北电网的电力生产总碳强度始终最高，但是发电量增长速度明显慢于其他区域，到2017年成为电力生产规模和排放规模最小的区域电网。③ 华东电网和西北电网的电力生产总碳强度下降速度落后于全国平均水平，总碳强度由2003年优于全国平均水平演变为2017年劣于全国平均水平。其中，华东电网2003—2010年电力生产总碳强度下降了133.28 gCO2/kWh，降幅仅次于华中电网，但是2010—2017年降幅仅有85.25 gCO2/kWh，是唯一电力生产总碳强度降幅收窄的区域。而西北电网虽然电力生产总碳强度变化较小，但2017年发电量快速增长到2003年的5.86倍，导致电力生产碳排放量快速增加，至2017年已超过东北电网和南方电网。
利用泰尔指数进一步反映各区域电网内及区域电网间的城市电力生产总碳强度差异的变化（表2）。① 从总体上看，2003—2017年中国城市电力生产总碳强度的总体泰尔指数从0.0876增加至0.1803，说明城市间电力生产总碳强度的差异在不断扩大。② 对比区域电网内和区域电网间的泰尔指数可知，区域内部差异是导致中国城市电力生产总碳强度差异的主要原因，其泰尔指数对总体的贡献度始终在75%以上。③ 从各区域来看，华东电网的区域泰尔指数始终明显低于其他区域，说明华东电网内城市的电力生产总碳强度差异最小；华中电网和南方电网的区域泰尔指数在研究期内持续上升，到2017年均明显高于其他区域，说明华中电网和南方电网内的城市差异非常突出。综合上述分析结果，不难发现中国城市间电力生产总碳强度的时空差异十分显著，这充分印证了城市尺度研究的必要性。
表2 2003—2017年区域电网内及区域电网间电力生产总碳强度泰尔指数

Tab. 2 Thiel index of ACI within and between regional power grids of China, 2003-2017

2003年 2010年 2017年
全国 0.0876 0.1220 0.1803
区域电网内 0.0780(89.09%) 0.1033(84.67%) 0.1379(76.52%)
区域电网间 0.0096(10.91%) 0.0187(15.33%) 0.0423(23.48%)
东北电网 0.1477 0.1808 0.2279
华北电网 0.1075 0.0801 0.1022
华东电网 0.0512 0.0426 0.0548
华中电网 0.1992 0.2811 0.4287
南方电网 0.1119 0.2141 0.3947
西北电网 0.1461 0.1883 0.1383

注：括号中数字表示贡献度。

3.2 时空演化特征

以200 gCO2/kWh为间隔，将城市电力生产总碳强度划分为8个等级，并进行可视化处理。2003—2017年中国城市电力生产总碳强度呈整体下降趋势，但东高西低、北高南低的空间分布特征始终保持不变（图3）。① 从高值区来看，2003年总碳强度超过1200 gCO2/kWh的城市共有72个，主要出现在东北地区、山西、河南和安徽。这些地区拥有丰富的煤炭资源，形成了粗放的能源消费模式，煤电生产技术水平落后、能耗水平较高，从而导致了较高的电力生产总碳强度。随着电力技术水平提升、非煤电力发展以及环境规制政策限制，上述地区电力生产总碳强度呈明显下降趋势，其中有90%以上的城市电力生产总碳强度在2017年降至1200 gCO2/kWh以下，但由于这些地区高度依赖火电，电力清洁化水平较低，其总碳强度仍明显偏高。② 从低值区来看，2003年电力生产总碳强度低值区的范围较小，主要集中在四川和云南，这是由于川滇地区水能资源丰富，前期的大规模水电开发显著提升了电力生产清洁化水平。2017年城市电力生产总碳强度的低值区扩展到长江中上游地区，以及以青海省为代表的西北地区。前者主要得益于长江流域水电的进一步发展，后者则源于风光资源的大规模开发，从而大幅提升了电力生产的清洁化水平，显著降低电力生产总碳强度。③ 尽管绝大多数城市电力生产总碳强度呈下降趋势，但有55个城市2017年的电力生产总碳强度高于2003年水平。其中，48个城市在2003年没有火电生产活动或火电占比较低，电力生产总碳强度明显低于全国平均水平，此后电力生产总碳强度随火电生产活动出现或比例提升而增加。另有鄂尔多斯、鹤岗、淮北、铁岭和邯郸5个城市，电力生产总碳强度在高于全国平均水平的基础上波动上升，而毕节、六盘水两市的电力生产总碳强度持续增加，表明煤炭资源富集地区的电力生产部门降碳难度较大。
图3 2003—2017年中国城市电力生产总碳强度的时空分布

注：基于自然资源部标准地图服务网站GS(2020)4630号标准地图制作，底图边界无修改。

Fig. 3 The spatiotemporal distribution of ACI in China's cities from 2003 to 2017

本文进一步对比分析“胡焕庸线”东南半壁、西北半壁及“博台线”东北半壁、西南半壁的发电总量、电力生产碳排放量和电力生产总碳强度水平。以2017年为例（表3），“胡焕庸线”两侧发电总量的差异明显高于“博台线”两侧，碳排放总量差异略高于“博台线”两侧；但从电力生产总碳强度来看，“博台线”两侧差异却更加显著；2003年和2010年亦是如此。上述结果说明电力生产总碳强度的空间分布格局不同于发电量、碳排放量以及其他人口、经济等传统指标，以“博台线”为分界线形成了较明显的东北—西南分异，这种分异规律的形成与资源禀赋、技术水平、电力结构等多方面因素有关。
表3 2017年“胡焕庸线”及“博台线”两侧发电总量、碳排放总量及电力生产总碳强度对比

Tab. 3 Comparison of total electricity generation, total CO2 emissions and ACI on both sides of the Hu Huanyong Line and Bole-Taipei Line in 2017

“胡焕庸线” “博台线”
东南半壁 西北半壁 差值 东北半壁 西南半壁 差值
发电总量(TWh) 5159.96 1082.13 4077.83 3992.05 2250.03 1742.02
碳排放总量(MtCO2) 3210.40 765.20 2445.20 3140.52 835.08 2305.45
电力生产总碳强度(gCO2/kWh) 622.17 707.13 84.95 786.69 371.14 415.55

3.3 空间集聚态势

利用Moran's I指数检验中国城市电力生产总碳强度的空间自相关性，结果显示3个年份的Moran's I指数均为正值，且通过1%水平的显著性检验，表明中国城市的电力生产总碳强度分布具有显著的空间相似性特征。Moran's I指数由2003年的0.18上升至2010年的0.24，至2017年达到0.35，表明城市电力生产总碳强度的空间集聚程度在加速提升。
通过LISA图分析城市电力生产总碳强度的空间集聚特征（图4）。整体而言，城市电力生产总碳强度呈低—低集聚（L-L）与高—高集聚（H-H）两级分化的显著特征。“博台线”西南半壁的城市以低—低集聚型为主，且集聚规模在研究期内显著扩大；东北半壁的城市以高—高集聚型为主，至2017年形成东北、华北2大片区。具体而言：① 2003年低—低集聚型主要集中分布于川西、滇西区域，其次在华南、东南地区分散了若干小规模片区；至2017年，低—低集聚型规模更大、更集中，形成以青海、四川、云南为主的大规模低—低集聚区域，而分散于东南地区的零散集聚区消失。② 2003年高—高集聚型主要集中分布于东北地区，少数分布在华北和中部地区；至2017年围绕华北地区的集聚组团显著扩张，形成以陕西、山西、蒙西、河北、河南为主的大规模高—高集聚区域；蒙东地区的高—高集聚区逐步萎缩，而东北东部地区逐步演变为高—高集聚型。
图4 2003—2017年中国城市电力生产总碳强度LISA图

注：基于自然资源部标准地图服务网站GS(2020)4630号标准地图制作，底图边界无修改。

Fig. 4 The LISA distribution of ACI in China's cities, 2003-2017

在全国电力生产结构转型的大背景下，低—低集聚区范围逐渐扩大，表明中国城市电力生产总碳强度逐渐呈现出以点带面的良好发展趋势。然而，高—高集聚区范围亦在扩大，城市数量由2003年的38个上升至2017年的66个，甚至反超了低—低集聚型。这是由于部分地区依旧高度依赖燃煤发电，电力生产总碳强度下降的效果相较于其他地区并不明显，特别是东北和华北两处高—高集聚区，在未来电力降碳的过程中应重点关注。

4 中国城市电力生产总碳强度的影响因素

4.1 电力系统因素

利用IDA-LMDI分解法对2003—2010年及2010—2017年中国电力生产总碳强度变化的电力系统驱动因子进行解析。从整体分解结果看（图5）：① 火电能耗因子（ΔVf）是2003—2010年电力生产总碳强度下降的主导因素，由火电能耗下降导致的全国电力生产总碳强度的下降占总变动的93.44%，2010—2017年这一份额降至35.82%。② 发电结构因子（ΔVp）在2010—2017年替代火电能耗因子成为电力生产总碳强度下降的最主要影响因素，影响效果从2003—2010年的-28.05 gCO2/kWh扩大到-81.61 gCO2/kWh。③ 不同种类化石燃料占比变化的影响效果方向各异，在2003—2010年间差异尤为显著；2003—2010年煤炭（ΔVq1）占比的提高导致电力生产总碳强度上升57.03 gCO2/kWh，剔除石油（ΔVq2）和天然气（ΔVq3）占比同步下降的影响，最终化石燃料组合因子（ΔVq）的累计效应为20.92 gCO2/kWh，即煤电占比提升抑制了全国电力生产总碳强度的下降；2010—2017年全国以煤炭为主的化石燃料组合结构基本保持稳定，化石燃料组合因子对电力生产总碳强度变动的影响很小，仅有-3.96 gCO2/kWh。④ 地理效应因子（ΔVg）对电力生产总碳强度的影响始终较弱，2003—2010年仅0.99 gCO2/kWh，2010—2017年变为-13.78 gCO2/kWh。
图5 2003—2010年及2010—2017年整体分解结果

Fig. 5 Overall performance of driving factors in the IDA-LMDI analysis during 2003-2010 and 2010-2017

将各个驱动因子的效应进一步分解到城市尺度，并进行统计特征分析（表4）及可视化处理（图6），不同驱动因子的影响效果呈现出明显的时空差异。
表4 城市尺度分解结果的统计特征

Tab. 4 Statistical characteristics of IDA-LMDI analysis results at the city scale

ΔVf ΔVp ΔVq1 ΔVg
T1 T2 T1 T2 T1 T2 T1 T2
负值占比(%) 72.14 80.71 48.57 83.93 62.14 53.57 50.00 53.93
最大值(gCO2/kWh) 2.26 3.68 1.84 1.31 11.09 1.42 11.49 11.61
最小值(gCO2/kWh) -14.33 -2.44 -9.46 -5.73 -1.38 -3.15 -13.09 -6.90
平均值(gCO2/kWh) -0.32 -0.20 -0.10 -0.29 0.20 -0.04 0.00 -0.05
标准差 1.26 0.60 0.77 0.70 1.05 0.26 2.20 1.59

注：T1、T2分别代表2003—2010年、2010—2017年。

图6 2003—2017年中国城市尺度分解结果的时空分布

注：基于自然资源部标准地图服务网站GS(2020)4630号标准地图制作，底图边界无修改。

Fig. 6 Distribution of IDA-LMDI analysis results at the city scale, 2003-2017

（1）火电能耗因子。2003—2010年城市尺度火电能耗因子效应的极差达到16.59 gCO2/kWh，标准差为1.26，2010—2017年上述指标分别降至6.12 gCO2/kWh和0.60，说明不同城市火电能耗因子的变动方向及效应在2003—2010年存在显著差异。2010—2017年80.71%的城市火电能耗下降，高于2003—2010年的72.14%，但是平均影响效果仅有-0.20 gCO2/kWh，不及2003—2010年的-0.32 gCO2/kWh，说明研究后期尽管更多城市的火电能耗呈下降趋势，但是产生的减排效应已渐弱。从空间分布来看（图6a、6b），2003—2010年以朔州、鄂尔多斯、淮北、锦州、张家口、乌兰察布为代表的部分北方煤炭资源型城市电力生产总碳强度显著增加，这是由于上述城市煤炭资源丰富、火电技术水平较差，粗放型的电力生产模式导致火电能耗上升明显，总碳强度随之提升。相较之下，以苏州、上海、石家庄、武汉、郑州、南京为代表的发达地区电力生产总碳强度下降明显，这主要受益于技术水平提升带来的火电能耗降低；长治、临汾等少数资源型城市的电力生产总碳强度也呈现了明显的下降态势，但这些地区既往火电能耗水平过高，技术升级空间充裕，最终表现为总碳强度的大幅降低。2010—2017年“博台线”东北半壁除东北地区外火电能耗上升城市数量明显减少，另有少量火电能耗上升城市散布于西南半壁，全国城市火电能耗水平趋于稳定。
（2）发电结构因子。2003—2010年仅有48.57%城市火力发电占比下降，2010—2017年占比变为83.93%，发电结构因子变动对电力生产总碳强度的平均效应则从2003—2010年的-0.10 gCO2/kWh扩大至2010—2017年的-0.29 gCO2/kWh。这说明2010—2017年非化石燃料发电在全国范围内普遍推广，成为电力生产总碳强度下降的主要驱动力。分城市来看（图6c、6d），2003—2010年间，发电结构因子效应为正值的地区主要出现在“博台线”西南半壁。这些城市普遍具有较好的水电开发历史，随着水电开发潜力的降低以及电力需求的上升，比水电更加高效稳定的火电生产规模扩大，这些城市发电结构清洁化水平降低，导致了电力生产总碳强度的上升。2010—2017年“博台线”西南半壁内火电占比上升的城市数量明显减少，说明风电、光伏等新能源电力的替代效果明显。
（3）化石燃料组合因子。由于不同化石燃料之间具有替代关系，而煤炭因子（ΔVq1）对电力生产总碳强度的效应较其他种类更为明显，因此以煤炭为代表对化石燃料组合因子的效应进行分析。2003—2010年城市尺度煤炭占比变化对电力生产总碳强度影响效果的极差为12.47 gCO2/kWh，标准差为1.05，2010—2017年上述指标分别降至4.56 gCO2/kWh和0.26，说明2003—2010年间不同城市化石燃料组合的变动较2010—2017年更加明显。从空间分布上看（图6e、6f），2003—2010年煤炭占比显著提高的地区主要分布在东南沿海、华北地区及辽宁省内。其中东南沿海主要受燃油燃气机组利用率下降影响。改革开放后东南沿海地区因电力供应短缺曾引入一批燃气燃油发电机组，因此2003年部分城市具有相对较高的油气发电占比，但由于油气供应短缺，燃油燃气机组经济性严重不足，2003—2010年间煤电机组建设速度和利用率大幅提升，替代原有燃油燃气机组，导致电力生产总碳强度上升。相较之下，华北及辽宁地区部分城市的煤炭消耗量占比提升主要与自身的高火电煤耗有关，煤电发电量扩大带来煤炭消耗量的显著提升。受数据估计方式变化影响，2010—2017年城市尺度化石燃料组合因子变化以省际变化替代，煤炭占比提高地区主要分布在“博台线”东北半壁，但变动幅度很小，所有城市煤炭因子对电力生产总碳强度的平均影响仅有-0.04 gCO2/kWh。
（4）地理效应因子。两个研究时段内，城市尺度地理效应因子对电力生产总碳强度的平均值极小，但极差和标准差始终保持较高水平，反映出不同城市发电量增长率的显著差异。从空间分布看（图6g、6h），地理效应因子变化而导致电力生产总碳强度显著增加的城市主要分布在“博台线”东北半壁，内蒙古地区尤为突出。这些城市普遍具有较高的电力生产总碳强度，同时伴随着电力生产份额的大幅提升，对全国电力生产总碳强度的下降产生了明显的抑制作用，说明这些地区应当成为未来电力部门节能降碳的重点关注地区。
综上所述，火电能耗因子是全国电力生产总碳强度的主导因素，前期电力生产总碳强度的下降主要依赖于对火电能耗的控制，但其影响效果在后期被发电结构因子超越，其他因子的作用效果始终较弱；电力系统因素的影响效果具有显著的空间分异，城市发电结构的变化方向在“博台线”两侧截然相反，化石燃料组合结构变动在东南沿海、华北和辽宁地区尤为突出，城市发电份额在内蒙古地区快速上升。

4.2 社会经济因素

分别对2003年、2010年及2017年数据开展空间滞后与空间误差回归分析，并对空间自回归项（rho）及空间误差项（lambda）进行检验，基于STIRPAT模型的空间回归分析检验结果如表5所示。2003年和2010年空间自回归项始终在1%的水平上显著，但空间误差项均不显著，且无法通过卡方检验及似然比检验；2017年空间自回归项和空间误差项均在1%的显著性水平上显著，综合AIC统计量及相关系数平方可知，空间滞后模型拟合效果略优于空间误差模型。由此可知，城市电力生产总碳强度及其解释变量存在显著的空间滞后效应。不同年份的基于STIRPAT模型的空间滞后回归结果如表6的模型Ⅰ、Ⅲ、Ⅴ所示，此外增加模型Ⅱ、Ⅳ、Ⅵ的结果，用于验证环境库兹涅茨曲线的成立与否。
表5 基于STIRPAT模型的空间回归分析检验结果

Tab. 5 Test results of spatial regression analysis based on STIRPAT model

回归模型 2003年 2010年 2017年
SLM SEM SLM SEM SLM SEM
rho 0.045*** 0.047*** 0.078***
lambda 0.015 0.010 0.143***
Wald test 11.275*** 1.073 14.645*** 0.916 50.251*** 92.404***
LR test 11.078*** 1.718 14.318*** 1.281 46.668*** 59.039***
LM test 10.138*** 6.432** 13.802*** 6.814** 45.867*** 46.841***
AIC 1829.508 1838.868 1709.554 1730.151 1615.438 1603.068
Squared correlation 0.318 0.292 0.371 0.341 0.369 0.206

注：***、**和*分别代表回归结果在1%、5%和10%的显著性水平显著，下同。

表6 空间滞后模型估计结果

Tab. 6 Estimation results of spatial lag model

2003年 2010年 2017年
模型Ⅰ 模型Ⅱ 模型Ⅲ 模型Ⅳ 模型Ⅴ 模型Ⅵ
lnPD 1.186***(4.37) 0.632**(2.43) 0.195(0.90)
lnUR 3.039***(5.15) 3.985***(4.81) 3.361***(4.24)
lnINV -1.043**(-2.13) -1.164**(-2.44) -0.455(-1.43)
lnINDP 0.534*(1.84) 0.653**(2.28) -0.030(-0.11)
lnRDP 0.271(1.20) 0.338**(2.28) 0.323**(2.42)
lnGDPP 1.913***(5.54) 4.369***(7.41) 1.853*(1.85)
(lnGDPP)2 -1.823***(-4.86) -1.549***(-4.09) -0.111(-0.25)
_cons -14.425***(-5.75) 4.403***(9.52) -16.082***(-5.53) 1.978***(5.21) -12.783***(-4.48) 0.734(1.34)

注：括号中的数值为t检验值。

（1）人口因素。从人口密度来看，2003年和2010年人口密度的回归系数分别在1%和5%的显著性水平上显著，人口密度每上升1%将分别导致电力生产总碳强度上升1.186%和0.632%，2017年人口密度的回归系数不显著。这说明前期人口密度的上升会导致电力生产总碳强度的增加，但影响效果逐步削弱。从城镇化率来看，城镇化率的回归系数始终在1%的显著性水平上显著，城镇化率每提升1%对电力生产总碳强度提升效果在3%~4%之间，始终高于其他影响因素。这说明城镇化率的提升是导致电力生产总碳强度增加的重要因素。
（2）富裕度因素。从投资水平来看，人均固定资产投资的回归系数始终为负，但仅有2003年和2010年在10%的显著性水平上显著，人均固定资产投资每提高1%将分别使电力生产总碳强度下降-1.043%和-1.164%。这说明前期增加人均固定资产投资能够导致电力生产总碳强度的同比例下降。从产业结构角度来看，人均工业增加值的回归系数在2003年和2010年分别在10%和5%的显著水平上显著为正，人均工业增加值每提高1%将导致电力生产总碳强度分别增加0.534%和0.653%，但人均工业增加值的回归系数在2017年不显著。这说明前期提高人均工业增加值将一定程度上导致电力生产总碳强度的增加。
（3）科技水平因素。人均R&D经费投入的回归系数始终为正，仅有2010年和2017年在5%的显著性水平上显著，人均R&D经费投入提高1%将导致电力生产总碳强度分别增加0.338%和0.323%。这说明在研究后期提高人均R&D经费投入会导致电力生产总碳强度的小幅增长。
（4）环境库兹涅茨曲线假说检验。2003年和2010年，人均GDP的回归系数为正，人均GDP平方项的回归系数为负，均在1%的显著性水平上显著。但2017年仅有人均GDP的回归系数在10%的显著性水平上显著为正，人均GDP平方项的回归系数不显著，人均GDP每增长1%导致电力生产总碳强度同步增长1.853%。这说明电力生产总碳强度和人均GDP在2003年和2010年存在倒“U”型曲线关系，即符合环境库兹涅茨曲线理论假设；而2017年则表现为线性正相关关系，即不符合环境库兹涅茨曲线理论假设。
总的来看，城镇化率始终是电力生产总碳强度的重要影响因素，高城镇化率往往伴随着高电力生产总碳强度；其他因素的作用效果则具有阶段性特征，前期人口密度、人均工业增加值和人均固定资产投资具有显著影响，而随着社会经济发展人均R&D经费投入演化为主要影响因素；环境库兹涅茨曲线假说可以在一定程度上解释人均GDP与电力生产总碳强度的关系，但这种倒“U”型曲线关系可能因为能源技术的进步而被突破，这一规律有待后文更深入地探讨。
除电力系统因素和社会经济因素外，自然地理条件也是电力生产总碳强度的重要影响因素。就资源禀赋而言，西南地区水能充沛，西北地区风能及太阳能资源丰富，上述地区可再生电力的大规模发展促进发电结构清洁化水平的提升，进而降低电力生产总碳强度。就地形地貌而言，海拔较高及坡度较陡地区的人口密度及城镇化率普遍偏低，这些地区火电需求较小，且能够为可再生能源电力发展提供充足的空间，从而促进电力生产总碳强度的下降。上述自然地理条件因素直接或间接作用于电力生产总碳强度，与电力系统因素和社会经济因素相互关联。

5 讨论

5.1 电力生产总碳强度影响机制

结合实证结果及理论分析，进一步凝练2003—2017年中国城市电力生产总碳强度时空演化的影响机制。本文认为人口、富裕度、科技水平等社会经济因素通过电力需求、电力技术、电力政策、清洁电力发展空间等要素的传导机制，改变化石燃料组合、火电能耗、发电结构等电力系统特征，最终表现为电力生产总碳强度的差异化时空分布及演变（图7）。
图7 电力生产总碳强度时空演变的影响机制

Fig. 7 The mechanism influencing spatial and temporal evolution of ACI

对传导机制进行细化分析：① 从电力需求来看，既有研究已经证实人口[27-28]、城镇化率[29-30]、投资[31]和工业产值[32-33]对电力需求的正向影响，高电力需求地区将布局更多效率高、经济性好的火电，从而导致电力生产总碳强度上升。相比之下，科技水平与电力需求两者间存在更为复杂关系：科技水平的提升一方面可以通过提高特定部门的用电效率来抑制电力需求，另一方面也会因为电气化水平和经济活动水平的提高而导致电力需求增加，即表现为“反弹效应”[34-35]，这可以解释人均R&D经费投入的回归系数后期显著为正的实证结果。② 从电力技术来看，在人口规模大、富裕程度高、科技投入多的地区，技术相对优势、环境规制压力、成本控制需求将促进火电技术进步及电力生产设施更新换代，从而降低电力生产总碳强度。但是这些社会经济特征在促进电力技术发展的同时也提高了电力需求，因此在实证中对电力生产总碳强度的影响表现出阶段性变化及方向性差异。③ 从电力政策来看，社会经济因素的空间异质特征导致了差异化的电力规划布局、价格政策和扶持手段。例如，2010年以前针对东南沿海等高城镇化率、高人均GDP的工业化地区的发电燃油补贴政策、核电规划布局，2010年后分区的风电、光伏标杆上网电价补贴制度、以及面向集中连片贫困地区的光伏发电扶贫政策等。上述政策对化石燃料组合情况以及电力结构产生重要影响，进而向不同方向改变电力生产总碳强度。④ 从清洁电力发展空间来看，高人口密度、城镇化率及经济活动水平地区既不是风、光、水资源富集地区，又因为土地资源短缺而具有较高的清洁电力开发成本[36]，因此严重制约清洁电力发展空间，不利于电力生产总碳强度的降低。
上述传导要素不仅受到社会经济因素的作用，彼此之间也相互影响。例如，高电力需求将推动电力促进政策的出台，推动电力技术进步，并将由于偏好效率更高的火力发电而挤压清洁电力发展空间，最终综合作用于电力系统。在社会经济因素、传导中介及电力系统特征3个层级间的复杂关系作用下，电力生产部门的总碳强度呈现显著的时空差异。

5.2 关于环境库兹涅茨曲线假说的讨论

环境库兹涅茨曲线假说是指环境质量与人均GDP之间呈倒“U”型曲线关系，其传统解释因素包括规模效应、结构效应、技术效应、环境质量的收入弹性及贸易[37]。本文的实证结果表明，2003年和2010年电力生产总碳强度和人均GDP之间的关系符合环境库兹涅茨曲线假说。如图8所示，在这一研究期内，人均GDP从较低水平开始提升会导致电力需求规模迅速扩大，由于技术水平和环境规制政策的不足，高排放强度的火电是电力供应的主要形式，从而导致电力生产总碳强度的上升。但当人均GDP达到一定水平后，经济的进一步发展伴随着产业结构的升级，带来电力技术的进步和环保意识的提升，促进了电力去煤化、低碳化发展，甚至通过电力交易实现排放转移，从而抵消需求上涨的规模效应，实现电力生产总碳强度的下降。
图8 电力生产总碳强度与人均GDP的关系及影响因素

Fig. 8 The relationship and influencing factors between ACI and per capita GDP

2017年电力生产总碳强度和人均GDP之间的关系不符合环境库兹涅茨曲线的假设，本文认为其主要原因是新能源电力作为一种突变因素，突破了适用于火力发电的传统解释框架。2010年后中国风电、光伏快速发展，增加发电量却不增加碳排放量，对于降低电力生产总碳强度的效果非常明显。但是如前文所述，经济发达地区风光资源禀赋较弱、可再生能源支持政策较少，且经济发展将进一步挤压清洁电力发展空间，即高人均GDP表现出对可再生能源发展的抑制作用。因此，随着人均GDP的持续增长，在火电为主时代具有明显减排效果的结构效应、技术效应、收入弹性等效应，将不及其对新能源电力的抑制效应，电力生产总碳强度将持续升高，无法复现倒“U”型曲线走势。
未来电力生产总碳强度与人均GDP的关系仍有待进一步论证。在可预见的未来，若火电部门的碳捕获、利用与封存技术（即CCS、CCUS技术）实现产业化的技术突破，则高人均GDP地区可以通过这一技术路径实现电力生产总碳强度的快速下降；亦或是随着储能技术、电力远距离传输技术的进一步突破，以及电力市场壁垒的解除，高人均GDP地区可以通过外购绿色电力、淘汰本地高耗能火电部门，实现本地电力生产总碳强度的快速下降。在上述路径下，未来电力生产总碳强度与人均GDP的关系有可能仍符合环境库兹涅茨曲线（图7）。总而言之，新能源和新技术的快速发展不可避免地对传统理论假说及其解释框架提出挑战，值得持续研究跟进。

6 结论

本文以中国城市电力生产总碳强度为研究对象，对其时空演化及影响因素进行了量化研究，并对环境库兹涅茨曲线假说进行了深化探讨。主要研究结论如下：
（1）2003—2017年中国电力生产总碳强度整体呈现加速下降趋势。城市间电力生产总碳强度的时空差异持续扩大，主要由各区域电网的内部差异导致，区别于发电量、碳排放量等指标，以“博台线”为分界线形成了较明显的东北—西南分异格局。城市电力生产总碳强度的空间集聚程度加速提升，“博台线”西南半壁的城市以低—低集聚型为主，且集聚规模在研究期内显著扩大；“博台线”东北半壁的城市以高—高集聚型为主，至2017年形成东北、华北两个集聚组团。
（2）从电力系统因素来看，火电能耗因子是2003—2010年电力生产总碳强度下降的主导因素，贡献率达到93.44%。2010—2017年发电结构因子以52.73%的贡献率，超过火电能耗因子成为电力生产总碳强度下降的重要影响因素。化石燃料组合因子仅2003—2010年综合表现为对整体电力生产总碳强度下降的具有一定抑制作用，地理效应因子则在2010—2017年综合表现为对整体电力生产总碳强度下降具有微弱的促进作用。城市尺度下，各因子的变动方向和影响效果具有明显的时空差异。
（3）从社会经济因素来看，城镇化率始终是导致电力生产总碳强度上升的重要因素；2003和2010年人口密度和人均工业增加值与电力生产总碳强度存在显著正相关关系，人均固定资产投资与电力生产总碳强度存在显著负相关关系；2010年和2017年人均R&D经费投入的提高会导致电力生产总碳强度小幅提升。对其作用机制进行凝练发现，各项社会经济因素通过作用于电力需求、电力政策、电力技术、清洁电力发展空间的复杂系统，从而引起电力系统的技术及结构变化，最终导致城市电力生产总碳强度的差异化演变。
（4）基于环境库兹涅茨曲线理论假设，电力生产总碳强度和人均GDP间在2003和2010年存在倒“U”型曲线关系，符合规模、结构、技术效应及收入弹性、电力贸易的传统解释框架。但随着新能源电力的快速发展，到2017年适用于火力发电的传统解释框架被突破，高人均GDP对新能源电力的抑制效应明显，因此电力生产总碳强度和人均GDP在较弱的置信水平上表现为正相关关系。未来若CCUS或远距离传输等技术实现突破，则电力生产总碳强度和人均GDP之间有望回归倒“U”型曲线关系。
电力生产部门是中国实现“双碳”目标的关键部门，基于上述结论本文提出以下政策建议：① 电力生产部门节能降碳政策设计应更多地考虑空间异质性，重点关注东北和华北地区的高电力生产总碳强度的集聚组团、电力生产总碳强度与发电量双高的火电供应基地以及能源消费模式粗放的煤炭资源富集地区，从而平衡城市间电力生产总碳强度的巨大差异。② 促进新能源电力的合理布局、推进远距离输电技术研发及基础设施建设、优化电力市场交易，从而缓解可再生能源发展与城镇化、富裕度、科技水平的互斥作用，实现经济发达及人口密集地区与新能源资源富集地区的协同降碳。
面对能源转型加速的时代背景，后续研究应持续跟踪电力技术突变，关注由此导致的“电力—环境—经济”系统关系演化，不断更新修正相关理论框架。此外，本文重点关注了真实产生碳排放的电力生产端，但实际上电力的传输和消费环节同样重要，上述环节将导致隐含碳在生产地和消费地之间转移，产生碳排放责任分配难题，这将是下一步研究的重点。

References

Publishing order | Descend order by publishing year | Descend order by cited within
[1]
He J K, Li Z, Zhang X L, et al. Towards carbon neutrality: A study on China's long-term low-carbon transition pathways and strategies. Environmental Science and Ecotechnology, 2022, 9: 100134. DOI: 10.1016/j.ese.2021.100134.

[2]
Liu Z, Deng Z, He G, et al. Challenges and opportunities for carbon neutrality in China. Nature Reviews Earth & Environment, 2022, 3(2): 141-155.

[3]
Ang B W, Su B. Carbon emission intensity in electricity production: A global analysis. Energy Policy, 2016, 94: 56-63.

DOI

[4]
Wang Y X, Yan Q Y, Li Z Y, et al. Aggregate carbon intensity of China's thermal electricity generation: The inequality analysis and nested spatial decomposition. Journal of Cleaner Production, 2020, 247: 119139. DOI: 10.1016/j.jclepro.2019.119139.

[5]
Ma S P, Liu Q Q, Zhang W Z. Examining the effects of installed capacity mix and capacity factor on aggregate carbon intensity for electricity generation in China. International Journal of Environmental Research and Public Health, 2022, 19(6): 3471. DOI: 10.3390/ijerph19063471.

[6]
Zhao Y, Cao Y, Shi X, et al. Structural and technological determinants of carbon intensity reduction of China's electricity generation. Environmental Science and Pollution Research, 2021, 28(11): 13469-13486.

DOI

[7]
Liu N, Ma Z J, Kang J D. A regional analysis of carbon intensities of electricity generation in China. Energy Economics, 2017, 67: 268-277.

DOI

[8]
Wang J F, He S T, Qiu Y, et al. Investigating driving forces of aggregate carbon intensity of electricity generation in China. Energy Policy, 2018, 113: 249-257.

DOI

[9]
Ang B W. LMDI decomposition approach: A guide for implementation. Energy Policy, 2015, 86: 233-238.

DOI

[10]
Goh T, Ang B W, Xu X Y. Quantifying drivers of CO2 emissions from electricity generation: Current practices and future extensions. Applied Energy, 2018, 231: 1191-1204.

DOI

[11]
Huang Rui, Wang Zheng, Ding Guanqun, et al. Trend prediction and analysis of influencing factors of carbon emissions from energy consumption in Jiangsu province based on STIRPAT model. Geographical Research, 2016, 35(4): 781-789.

DOI

[ 黄蕊, 王铮, 丁冠群, 等. 基于STIRPAT模型的江苏省能源消费碳排放影响因素分析及趋势预测. 地理研究, 2016, 35(4): 781-789.]

DOI

[12]
Liu Y S, Yan B, Zhou Y. Urbanization, economic growth, and carbon dioxide emissions in China: A panel cointegration and causality analysis. Journal of Geographical Sciences, 2016, 26(2): 131-152.

DOI

[13]
Wang Shaojian, Xie Zihan, Wang Zehong. The spatiotemporal pattern evolution and influencing factors of CO2 emissions at the county level of China. Acta Geographica Sinica, 2021, 76(12): 3103-3118.

DOI

[ 王少剑, 谢紫寒, 王泽宏. 中国县域碳排放的时空演变及影响因素. 地理学报, 2021, 76(12): 3103-3118.]

DOI

[14]
Wang Shaojian, Su Yongxian, Zhao Yabo. Regional inequality, spatial spillover effects and influencing factors of China's city-level energy-related carbon emissions. Acta Geographica Sinica, 2018, 73(3): 414-428.

DOI

[ 王少剑, 苏泳娴, 赵亚博. 中国城市能源消费碳排放的区域差异、空间溢出效应及影响因素. 地理学报, 2018, 73(3): 414-428.]

DOI

[15]
Liu Weidong, Tang Zhipeng, Xia Yan, et al. Identifying the key factors influencing Chinese carbon intensity using machine learning, the random forest algorithm, and evolutionary analysis. Acta Geographica Sinica, 2019, 74(12): 2592-2603.

DOI

[ 刘卫东, 唐志鹏, 夏炎, 等. 中国碳强度关键影响因子的机器学习识别及其演进. 地理学报, 2019, 74(12): 2592-2603.]

DOI

[16]
Wang Shaojian, Huang Yongyuan. Spatial spillover effect and driving forces of carbon emission intensity at city level in China. Acta Geographica Sinica, 2019, 74(6): 1131-1148.

DOI

[ 王少剑, 黄永源. 中国城市碳排放强度的空间溢出效应及驱动因素. 地理学报, 2019, 74(6): 1131-1148.]

DOI

[17]
Jiang Wanbei, Liu Weidong, Liu Zhigao, et al. Inequality and driving forces of energy-related CO2 emissions intensity in China. Progress in Geography, 2020, 39(9): 1425-1435.

DOI

[ 姜宛贝, 刘卫东, 刘志高, 等. 中国化石能源燃烧碳排放强度非均衡性及其演变的驱动力分析. 地理科学进展, 2020, 39(9): 1425-1435.]

DOI

[18]
Wang Zheng, Fan Jie. The characteristics and prospect of influencing factors of energy-related carbon emissions: Based on literature review. Geographical Research, 2022, 41(10): 2587-2599.

DOI

[ 王正, 樊杰. 能源消费碳排放的影响因素特征及研究展望. 地理研究, 2022, 41(10): 2587-2599.]

DOI

[19]
Wood R, Lenzen M. Zero-value problems of the logarithmic mean divisia index decomposition method. Energy Policy, 2006, 34(12): 1326-1331.

DOI

[20]
Ang B W, Liu N. Handling zero values in the logarithmic mean Divisia index decomposition approach. Energy Policy, 2007, 35(1): 238-246.

DOI

[21]
Dietz T, Rosa E A. Rethinking the environmental impacts of population, affluence and technology. Human Ecology Review, 1994, 1(2): 277-300.

[22]
Ehrlich P R, Holdren J P. Impact of population growth. Science, 1971, 171(3977): 1212-1217.

PMID

[23]
Zhou K L, Yang J N, Yang T, et al. Spatial and temporal evolution characteristics and spillover effects of China's regional carbon emissions. Journal of Environmental Management, 2023, 325: 116423. DOI: 10.1016/j.jenvman.2022.116423.

[24]
Liao C Y, Wang S G, Zhang Y Y, et al. Driving forces and clustering analysis of provincial-level CO2 emissions from the power sector in China from 2005 to 2015. Journal of Cleaner Production, 2019, 240: 118026. DOI: 10.1016/j.jclepro.2019.118026.

[25]
Wang J, Song C, Yuan R. CO2 emissions from electricity generation in China during1997-2040: The roles of energy transition and thermal power generation efficiency. Science of the Total Environment, 2021, 773: 145026. DOI:10.1016/j.scitotenv.2021.145026.

[26]
He Y, Xing Y T, Zeng X C, et al. Factors influencing carbon emissions from China's electricity industry: Analysis using the combination of LMDI and K-means clustering. Environmental Impact Assessment Review, 2022, 93: 106724. DOI:10.1016/j.eiar.2021.106724.

[27]
Lin B Q, Zhu J P. Chinese electricity demand and electricity consumption efficiency: Do the structural changes matter? Applied Energy, 2020, 262: 114505. DOI: 10.1016/j.apenergy.2020.114505.

[28]
Wu L, Gao X, Xiao Y, et al. Using a novel multi-variable grey model to forecast the electricity consumption of Shandong province in China. Energy, 2018, 157: 327-335.

DOI

[29]
Yuan J H, Zhao D F. A panel empirical modeling on the driving factors of provincial electricity consumption in China. Environmental Science and Pollution Research, 2022, 29(7): 10345-10356.

DOI

[30]
Xie L Y, Yan H S, Zhang S H, et al. Does urbanization increase residential energy use? Evidence from the Chinese residential energy consumption survey 2012. China Economic Review, 2020, 59: 101374. DOI: 10.1016/j.chieco.2019.101374.

[31]
Fang D B, Hao P, Yu Q, et al. The impacts of electricity consumption in China's key economic regions. Applied Energy, 2020, 267: 115078. DOI: 10.1016/j.apenergy.2020.115078.

[32]
Cui W C, Li J Y, Xu W T, et al. Industrial electricity consumption and economic growth: A spatio-temporal analysis across prefecture-level cities in China from 1999 to 2014. Energy, 2021, 222: 119932. DOI: 10.1016/j.energy.2021.119932.

[33]
Li K, Yuan W H. The nexus between industrial growth and electricity consumption in China: New evidence from a quantile-on-quantile approach. Energy, 2021, 231: 120991. DOI: 10.1016/j.energy.2021.120991.

[34]
An H, Xu J J, Ma X J. Does technological progress and industrial structure reduce electricity consumption? Evidence from spatial and heterogeneity analysis. Structural Change and Economic Dynamics, 2020, 52: 206-220.

DOI

[35]
Lin B Q, Zhao H L. Technological progress and energy rebound effect in China's textile industry: Evidence and policy implications. Renewable and Sustainable Energy Reviews, 2016, 60: 173-181.

DOI

[36]
Ioannidis R, Koutsoyiannis D. A review of land use, visibility and public perception of renewable energy in the context of landscape impact. Applied Energy, 2020, 276: 115367. DOI: 10.1016/j.apenergy.2020.115367.

[37]
Sarkodie S A, Strezov V. A review on Environmental Kuznets Curve hypothesis using bibliometric and meta-analysis. Science of the Total Environment, 2019, 649: 128-145.

DOI

Options
Outlines

/

〈 〉