引用本文
王劲峰, 葛咏, 李连发, 孟斌, 武继磊, 柏延臣, 杜世宏, 廖一兰, 胡茂桂, 徐成东. 地理学时空数据分析方法. 69(9): 1326-1345
WANG Jinfeng, GE Yong, LI Lianfa, MENG Bin, WU Jilei, BO Yanchen, DU Shihong, LIAO Yilan, HU Maogui, XU Chengdong. Spatiotemporal data analysis in geography. Acte Geographica Sinica, 69(9): 1326-1345  
Permissions
Copyright©2014, 《地理学报》编辑部
本文是开放获取期刊文献，在以下情况下可以自由使用：学术研究、学术交流、科研教学等，但不允许用于商业目的.
地理学时空数据分析方法
王劲峰1, 葛咏1, 李连发1, 孟斌2, 武继磊3, 柏延臣4, 杜世宏5, 廖一兰1, 胡茂桂1, 徐成东1
1. 中国科学院地理科学与资源研究所, 北京 100101
2. 北京联合大学应用文理学院, 北京 100191
3. 北京大学人口研究所, 北京 100871
4. 北京师范大学遥感与地理学院, 北京 100875
5. 北京大学地球与空间科学学院, 北京 100871

作者简介：王劲峰 (1965-), 男, 研究员, 中国地理学会会员 (BJ1566), 从事地理信息科学的理论创新和实践。E-mail: wangjf@igsnrr.ac.cn

基金:国家自然科学基金 (41023010); 973课题 (2012CB955503); National Natural Science Foundation of China, No.41023010; The National Basic Research Program of China, No.2012CB955503
摘要

随着地理空间观测数据的多年积累,地球环境、社会和健康数据监测能力的增强,地理信息系统和计算机网络的发展,时空数据集大量生成,时空数据分析实践呈现快速增长。本文对此进行了分析和归纳,总结了时空数据分析的7类主要方法,包括：时空数据可视化,目的是通过视觉启发假设和选择分析模型;空间统计指标的时序分析,反映空间格局随时间变化;时空变化指标,体现时空变化的综合统计量;时空格局和异常探测,揭示时空过程的不变和变化部分;时空插值,以获得未抽样点的数值;时空回归,建立因变量和解释变量之间的统计关系;时空过程建模,建立时空过程的机理数学模型;时空演化树,利用空间数据重建时空演化路径。通过简述这些方法的基本原理、输入输出、适用条件以及软件实现,为时空数据分析提供工具和方法手段。

关键词: 时空数据; 时空格局; 时空过程; 时空机理; 样本; 对象总体; 大数据
Spatiotemporal data analysis in geography
WANG Jinfeng1, GE Yong1, LI Lianfa1, MENG Bin2, WU Jilei3, BO Yanchen4, DU Shihong5, LIAO Yilan1, HU Maogui1, XU Chengdong1
1. LREIS, Institute of Geographic Sciences and Natural Resources Research, CAS, Beijing 100101, China
2. College of Applied Arts & Sciences of Beijing Union University, Beijing 100191, China
3. Institute of Population Research, Peking University, Beijing 100871, China
4. School of Geography, Beijing Normal University, Beijing 100875, China
5. School of Earth and Space Science, Peking University, Beijing 100871, China
Abstract

Following the emergence of large numbers of spatiotemporal datasets, the literatures related to spatiotemporal data analysis increase rapidly in recent years. This paper reviews the literatures and practices in spatiotemporal data analysis, and classifies the methods available for spatiotemporal data analysis into seven categories: including geovisualization of spatiotemporal data, time series analysis of spatial statistical indicators, coupling spatial and temporal change indicators, detection of spatiotemporal pattern and abnormality, spatiotemporal interpolation, spatiotemporal regression, spatiotemporal process modelling, and spatiotemporal evolution tree. We summarized the principles, input and output, assumptions and computer software of the methods that would be helpful for users to make a choice from the toolbox in spatiotemporal data analysis. When we handle spatiotemporal big data, spatial sampling appears to be one of the core methods, because (1) information in a big data is often too big to be mastered by human physical brain, so has to be summarized by statistics understandable; (2) the users of Weibo, Twitter, internet, mobile phone, mobile vehicles are neither the total population nor a random sample of the total population, therefore, the big data sample is usually biased from the population, and the bias has to be remedied to make a correct inference; (3) the data quality is usually inconsistent within a big data, so there should be a balance between the variances of inferences made by using data with various quality and by using small but high quality data.

Keyword: spatiotemporal data; spatiotemporal pattern; spatiotemporal process; spatiotemporal mechanism; sample; target population; big data
1 引言

随着社会与经济调查与统计、对地观测技术、计算机网络和地理信息系统的快速发展和普及, 具有空间位置的自然环境与社会经济数据近几十年快速增长, 形成了海量的时空数据集[1]和时空大数据。依据文献分析, 目前科学研究对时空数据分析的理论方法探讨日益增多。如以时空分析为题目的专著有Modern Spatiotemporal Geostatistics[2]、Statistics for Spatio-Temporal Data[3]和Spatial Statistics and Spatio -Temporal Covariance Function and Directional Properties[4]等, 而时空分析实践论文更加广泛[5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17], 涉及各种各样的分析方法。截止2014年8月30日, 以“ 时空数据分析” 为关键词检索google有161万条、百度918万条; 以spatiotemporal analysis为检索词google有1230万条, Web of Science标题719条、主题8680条。专著自成体系, Modern Spatiotemporal Geostatistics[2]核心内容是贝叶斯最大熵理论 (BME), 在BME框架内可以融合一般知识, 例如牛顿定律和传染病SIR模型, 和专有知识, 例如具体数值等硬数据和取值范围等软数据。据此进行时空预测。Statistics for Spatio-Temporal Data[3]一书论述了三类方法：反应扩散方程、Kriging插值和贝叶斯层次回归模型。其中贝叶斯层次模型由数据模型、过程模型、和参数模型逐级嵌套而成。基于这些专著和文献, 本文试图通过对现有时空分析理论和实践进行梳理和分析, 归纳总结出时空数据分析的方法体系和主要工具。

作为地理学量化研究的工具, 空间统计方法基于统计学理论已经发展形成了相对完整的理论体系。借助统计学丰富严谨的数据分析方法, 时空数据分析有可能取得更加丰硕的成果。为地理学从统计学“ 借力” , 首先需要沟通地理学和统计学语言 (表1), 搭建两者连接的桥梁。地理学获取研究对象的数据, 据此推断研究对象的格局、过程和机理。空间统计学将研究区域 (如中国) 看作一个总体 (population); 而时空统计学将研究区域 (如中国)和研究时段 (如新中国成立以来) 看作一个总体。在统计学中, 总体由样本单元 (unit) 组成; 在空间统计学中, 样本单元为空间单元, 如中国近3000个县或960万个公里网格; 在时空统计学中, 样本单元为时空单元, 如中国近3000个县或960万个公里网格与1949-2014年逐年组合形成的县年或公理年单元。为获取数据, 需要从总体中抽取一个样本 (sample), 由有限个单元组成 (如在空间统计中随机抽取300个县, 抽样率为10%; 或在时空统计中抽取300个县并且从1949-2014年的65年中随机抽取10年, 其空间抽样率为10%, 时间抽样率为10/65 = 15%)。

表1 地理学与统计学名词比较 Tab. 1 Comparison between terms in geography and statistics

一个属性y (如GDP) 值随样本单元s和随时间t变化, 被看做是一个时空随机变量[3]。

{y(s, t):s∈Ds⊂Rd, t∈Dt⊂R}(1)

式中, Ds是感兴趣的空间域, Dt是感兴趣的时间域, R是实数, d是维度。一个时空样本的属性值被看做是这个随机变量在一个时空点 (s, t) 上的一次实现。在空间统计中, 一个随机抽取的样本 (300个县2014年GDP) 经统计方法 (如简单算术平均, 再被抽样率除) 推断总体参数 (得到2014年全国GDP总量), 并进一步推断总体背后的超总体的参数 (如全国逐年GDP), 需要对超总体的性质做某种假设, 一般需要使用基于模型的方法 (Model based)。总体被看做是超总体的一次实现。在时空统计中, 样本 (随机抽取的300个县, 随机抽取的10年的GDP) 经统计方法 (如时空插值, 再逐年汇总)推断总体参数 (如全国逐年GDP)。总体背后的超总体可能不是唯一的[18], 超总体可由过程机理, 研究目的和数学处理的方便程度来定义。目前, 时空过程的超总体尚不清楚。这几个概念大体的对应关系是：地学数据 (data)— 统计学样本 (sample); 地学格局 (pattern)— 统计学总体 (population); 地学过程 (process)— 统计学超总体 (superpopulation)。地理学分析立足于数据, 通过数据分析揭示的空间格局和过程, 讨论地理事物的规律和机理。统计学立足于变量, 由变量推断总体, 反演超总体的参数和性质。

空间数据分析、时间序列分析和时空数据分析的研究对象分别是空间数据、时间序列数据和时空数据。我们将输入或者输出为时空数据的各种分析称为时空分析。时空分析的目的是从时空数据中发现规律和异常、分析关联和探究机理, 并进行预警和预测。本文中, 我们首先回顾时空现象观测数据和变量, 以及时空现象产生的机理, 然后对时空数据分析的主要工具类型和适用条件进行梳理和归纳, 最后进行讨论和得到结论。

2 时空数据和时空变量

陆地、海洋、大气、生物、经济和社会现象, 乃至世界万物都具有地理空间分布 (s), 并且随时间 (t) 变化, 被观察并记录为时空数据。时空数据是时空变量的一次或有限次观测值。下文用y(s, t) 表示时空数据或时空变量。

2.1 时空数据

时空数据最直接的记录方式是时空二联表、地图时间序列和状态转换矩阵。

(1) 时空二联表 行表示空间维、列表示时间维, 单元格记录属性值。例如, 以全国34个省市自治区直辖市为34行, 1949-2014年共65年为65列, 单元格记录年度GDP数值, 可以反映我国GDP的时空变化。时空二联表可以完整记录时空各节点的观测值, 但是无法记录时空数据的空间拓扑关系。

(2) 地图时间序列 在各时间节点分别制作某属性专题图, 形成地图序列。例如北京18个区县2003年3月1日至30日逐日SARS新发病例分布图序列, 反映了这种传染病空间分布的时间演变。地图序列能够完整记录时空演化信息, 但是目前的GIS软件中尚缺少有效的时空数据结构来存储和操作这类数据[19]。

(3) 状态转换矩阵 行列分别代表两个时间节点上相同的状态变量, 单元格表示经过一个时间段, 所在行状态转换为所在列状态的量。例如2000-2010年中国耕地、林地、水体、草地、建设用地、和其他用地之间的相互转移量。转换矩阵可以完整记录了各状态之间的流转, 但在时间维度上, 只能局限于两个节点之间。

2.2 时空变量

数学和统计学建立了关于变量的理论。时空分析就是要借助统计学和数学, 通过研究观测样本y, 推断总体或超总体的参数和性质, 即地理学研究事物的格局、过程、规律和机理。时空数据推断总体可以是基于设计的或者基于模型的两个途径。

基于设计的统计推断方法 (design based)。先从总体中以某种方式 (设计) 抽取一定数量的样本, 每个样本单元有一个观测数值; 然后对样本进行统计, 推断总体。样本抽取的方式 (设计) 主要包括随机、系统、分层等。对于一个统计量, 即估算公式, 基于设计的统计估值及其误差随样本设计 (布置方式和密度) 变化而变化。在一定样本量的前提下, 随机或分层随机抽样能够保证样本统计推断总体是设计无偏的 (注意, 不能保证最优, 也就是不保证误差最小)。设计无偏在理论上与总体性质无关; 然而, 估值方差将随着空间相关性和分异性而发生变化。特别地, 当总体是分层异质的 (stratified heterogeneity), 并且样本小到没有覆盖所有的层 (strata) 时, 样本有偏于总体, 传统的统计推断结果将有偏于总体参数。此时, 若有无偏样本或全覆盖的相关辅助数据, 则可用专门算法纠偏, 从而得到无偏估计。

基于模型的统计推断方法 (model based)。假设每个时空格点的值都是一个时空随机变量, 观测值是其一次实现。为进行推断, 假设随机变量具有平稳性, 即各时空点数学期望相等。若不平稳, 则先分层 (stratification), 使层内平稳, 然后对时空变量加权来估计总体参数, 以估值误差最小为目标函数, 以估值无偏为约束, 求解样本权重。基于模型的统计估值及其误差在理论上与样点绝对位置无关。当研究对象性质与模型假设一致时, 基于模型的统计推断可以得到无偏最优估计 (BLUE)。当目标对象性质与模型假设不符时, 模型结果有误。

时空数据分析可以是基于设计的也可以是基于模型的, 结果可能相同或不同。可以根据研究目标 (总体或超总体)、对象性质 (独立同概率分布、空间自相关、空间分层)、以及样本 (布设位置和密度)选择恰当的方法。也可以对数据同时使用基于设计的和基于模型的方法, 但结果具有不同的含义[18], 需参见两种方法的定义和性质, 对结果进行解释。

2.3 变量类型

数据 (基于设计的观点) 或变量 (基于模型的观点) y(s, t) 可以是自然环境, 如温度、降水、水土流失; 经济与社会, 如人口、GDP、交通、疾病等, 以及人地关系, 如土地利用、生态价值、自然灾害等。

(1) 空间变量 当属性存在空间分异并且随时间稳定或不分辨时间, 即y(s, t) = y(s), 如中国地形三级阶地、胡焕庸人口线、气候带、生物区系等, 可以用空间分析方法[20, 21, 22]。

(2) 时间变量 当属性空间均质或不分辨空间差异, 即y(s, t) = y(t), 如区域CPI指数、北京逐年常住人口变化, 可以用时间序列分析方法。当存在空间分异但在分析时不予考虑, 将有可能导致生态谬误。

(3) 时空变量 当属性随空时皆变, 即y(s+u, t+τ ) ≠ y(s, t), 例如中国近3000个区县2008.3-2009.4各周手足口病病例数, 可使用时空分析方法[2, 3], 具体方法请见本文第4节。

(4) 状态变量 属性值变化到一定程度, 从量变产生质变, 状态或类型发生了变化。人们往往对质变, 也就是状态变化更感兴趣, 为此, 可以定义状态变量。状态变量反映格局、规律和大势。例如土地利用类型, 由于城市化而发生变化。一个城市的产业类型和发展阶段也会演化。

空间变量和时间变量是时空变量的特例, 这些变量的测量可以是比值量 (Ratio)、间隔量 (Interval)、顺序量 (Ordinal) 和名义量 (Nominal), 在统计学中分析方法有区别。比值量和间隔量常统称为数值量。地理学中状态 (包括名义量和顺序量) 变化是值得特别关注的, 特用状态变量。例如, 天气状态可以是下雨、多云、晴天; 而天气测量是温度、湿度、气压等数值量。

3 时空过程和时空机理

时空数据有限次地记录了时空过程, 时空过程是过程机理驱动的结果。如, 日地环绕、大陆漂移碰撞和万有引力等机理分别导致了地球气候的经纬度差异、海拔高程地带性和地壳物质分层和迁移等时空现象。自然环境演化等机理产生了生物和人类。进一步, 在自组织机制下, 生物圈发展和演化。时空过程在数学上可由若干时空变量按照过程机理关系表示, 在地理空间上表现为时空现象：

过程机理 — 在时空坐标系中表象→ 时空过程 (用时空变量关系表达) — 时空过程被观测记录→ 时空数据

时空数据分析的目的就是从时空数据出发, 运用各种时空分析工具, 溯源其时空过程乃至机理, 由样本推断总体或超总体的参数。如果时空数据来自于对时空过程有一定密集度的随机采样, 样本将蕴含了过程的所有时空规律、时空异常等信息, 我们称之为完备时空样本。如果时空样本不完备, 则首先需要基于抽样理论进行加密观测或纠偏[18]。本文假设数据集是完备的：

(完备) 时空样本 → 时空规律 + 时空异常 + 时空噪音

时空规律是时空过程中已经被人类认知和掌握的部分, 建立机理或统计模型, 可以预测预报; 时空异常是与人类已认识的规律有明显差异, 不能依据现有规律准确预期的部分; 时空噪音没有规律并且没有明显异常值, 目前尚不为人类所认知的部分。恰当利用分析工具, 对时空异常（如传染病）进行早期预警, 具有重要意义; 另一个努力的方向是从模型残差中提取更多的信息, 增强我们对时空异常的物理机制的理解, 转化为规律, 从而对其有所预期和掌握。

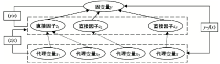
时空过程和机理以因变量y和影响因子z之间的联系 (y|z) 来表达。在地理学, 直接影响因子z往往难以获得, 常用的方法是寻找代理变量x[23], 建立因变量与代理变量的统计关系y = f(x)。代理变量x应当满足两个条件：一是与直接因子z尽量相关 (z|x), 可基于物理机制定性判断, 或基于相关分析定量选择; 二是全覆盖研究区域和研究时段 (图1)。例如, 新生儿出生缺陷发生风险 (y) 与环境污染暴露、遗传和营养等直接因子 (z) 有关, 而遗传和营养测量和调查成本高, 因此寻找其代理变量 (x), 如, 用以村庄为中心做不同距离缓冲区, 分别计算局域空间聚集性指标（Gi）来反映人们社会交往和通婚圈作为遗传代理因子[24], 用人均收入代理营养摄入水平。应当结合具体研究问题将代理变量图1具体化, 图1可以帮助选择代理变量, 理解过程机理, 并且用于解释统计结果。

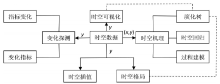
图1 代理变量图Fig. 1 Proxy variable diagram

4 时空分析工具

对于时空因变量数据 (y), 可以进行可视化探索分析、时空变化探测、时空格局识别、时空插值和补缺, 还可以通过影响因子 (x) 分析推测时空机理。其中, 时空机理的认知可以分为物理的 (过程建模)、统计的 (时空回归)和生物的 (演化树)。演化树还是一种可视化的手段, 实现属性空间和地理空间之间的二元协同感知。可以利用时空数据分析工具箱 (图2) 的主要内容和相互关系选择一个或多个工具, 从多角度探索、分析时空数据。

图2 时空数据分析工具箱Fig. 2 Spatial-temporal data analysis toolbox

4.1 时空可视化

时空可视化是以图的形式将时空数据展示出来[25], 时空可视化对于地理学的意义就如显微镜对于生物学的意义。人类视觉先将属性的位置依赖关系及其时间变化信息直接传入大脑, 人脑再根据直觉和形象思维进行知识推理和综合分析。相对于电脑, 人脑擅长处理非数值量, 虽然其处理过程尚不完全清楚。时空数据可视化作为统计数值分析的先导和补充, 提供背景信息和提示时空规律。主要有以下几种方法。

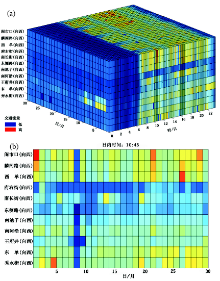
(1) 时空立方 时空立方可以是二维空间加时间维度, 也可以分别以两个时间分辨率为两个维度, 地理空间为第三维, 颜色表示属性值。例如, 图3a展示了北京长安街各主要路口 (纵轴) 在2002年11月共31天及每天24小时 (两个水平轴表示两个时间分辨率) 的交通流量 (颜色) (图3a)。图3b是图3a的在10:45的时间切片; 可以在不同维度上任意点作切片。该方法可以完全保留一维线性对象的空间拓扑关系。

图3 时空立方体Fig. 3 Space-time cube

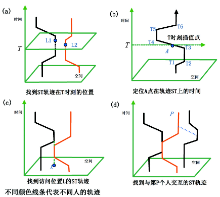
(2) 时空轨迹 以水平二维坐标表示地理空间, 以纵坐标表示时间, 时空轨迹将一个主体, 如人的时空运动轨迹用线连接起来[26]。图4在平面图上可视化了几个人的时空轨迹。图4a给定时间T, 定位两人的空间位置、空间距离和相对方位; 图4b给定地点A, 确定某人到达的时间; 图4c统计地点L的来客的时空路径; 图4d发现与人P有关其他人的时空路径[27]。时空轨迹已经成功运用于犯罪和疾病传染分析。

图4 时空轨迹[27]Fig. 4 Space-time trajectory[27]

(3) 时空剖面 分别以距某地物远近 (欧式或非欧距离) 和时间为两个水平维度, 以属性值为纵轴, 在纸质平面上表达的三维图案, 用以发现某属性与某地物的统计关联, 并且表达这种关系随时间的变化。例如, 从云南省玉溪市某区域的伤寒副伤寒发病率随城市排污渠远近的变化 (图5) 及这种关系随时间的变化[28], 可以发现存在视觉相关性。又如, 分别画出几个不同年份某城市地价距市中心远近变化的剖面图[29]。再如, 从欧洲1890-2010年各纬度带逐年温度年均温变化 (图6), 可以反映出欧洲1960年以来年均温升高的趋势, 并且这种趋势随纬度升高而加剧。

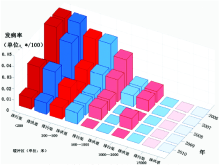图5 云南玉溪市伤寒副伤寒发病率与排污渠关系的时空变化[28]Fig. 5 Space-time variability of typhoid and paratyphoid incidence and sewer system[28]

图6 欧洲1888-2010年年均温随各纬度和逐年变化[30]Fig. 7 Annual mean temperature changes by latitudes in Europe from 1888 to 2010[30]

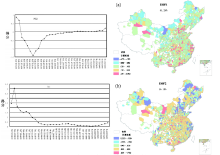
(4) 时空动画 利用计算机图形技术将地图序列的每一幅图片按时间帧连接并播放即生成时空动画, 完整地展示了所有时空信息。图7是我国各省2003年逐日SARS新发病例时空动画两个时间截图, 上图是时间过程, 下图是时空过程。一维的时间序列图不能解释对同一疫情的两个高峰, 而通过下面的时空过程表达, 就知道这两个高峰分别来自2003年初广州和春季北京及周边两个不同地区的SARS疫情爆发。

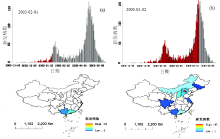图7 中国2003年SARS时空传播动画截图Fig. 7 Animation screenshots of SARS spatiotemporal spread in China in 2002-2003

(5) 虚拟现实 基于相似准则, 运用计算机虚拟现实技术将空间、时间和物体等比例缩小, 将研究对象、环境及其相互作用建立在计算机中[31], 各要素和参数可操作、加减和调控。犹如电子游戏, 使用者沉浸在地理虚拟现实之中, 进行各种仿真和模拟实验。虚拟现实最终有可能取代现在的GIS技术, 成为时空数据管理和分析的基本工具。

以上5种可视化方案可以展示时空数据的不同方面。其中时空轨迹是展示一个或多个个体时空运动的技术, 虚拟现实需要较高的硬件和软件配置。

4.2 指标变化

空间统计量随时间的变化序列。将时空变化看作是空间分布随时间变化, 在每个时间点分别做空间统计, 将其按时间先后次序连接起来, 反映空间统计指标变化。已有的许多空间统计指标, 如几何重心、最邻近距离[32]、BW统计、全局和局域的Moran's I和Getis G、Ripley K, 半变异系数、空间回归系数等[21, 22], 均可做时间维度分析。例如, 收集北京市18个区县2003年4月27日至5月7日各区县每日SARS新发病例, 计算每日北京SARS空间聚集指标Moran's I, 连接起来形成时间序列图8[33], 发现在5月1日前, SARS在空间缓慢扩散, 其后快速聚集收缩, 直至消亡。图9ab分别是中国中东部1456个县2008年5月1日 (第1周) 至2009年3月26日 (第47周) 每周平均气温和手足口病新发病人数的几何重心随时间迁移, 可见平均气温重心从第1周 (2008年5月1日)向东北方向移动, 至第8周 (2008年6月19日) 到达最东北端, 随后向西南折回; 手足口病重心从第1周 (2008年5月1日) 也向东北方向移动, 至第14周 (2008年7月31日) 到达最东北端, 随后也向西南折回。手足口病重心滞后平均气温重心7周[34], 图9ab中的最大最小值分别指全国周发病人数和全国周平均气温。

[33]

'>		图8 北京2003年4月27至5月7日SARS时空传播Moran's I指标逐日变化[33]Fig. 8 Moran's I of SARS incidences in Beijing changes in time, Beijing, April 27 to May 7, 2003[33]

图9 中国手足口病 (a) 和气温 (b) 2008年5月1至2009年3月19逐周几何重心轨迹[34]Fig. 9 Geometric center trajectories of (a) HFMD incidence and (b) temperature in China from May 1, 2008 to March 19, 2009[34]

“ 指标变化” 直接将空间统计运用于时空数据, 熟悉空间统计的读者不需要增加任何新的知识就可以进行时空数据分析。

4.3 变化指标

反映时空变化的综合指标, 用单一值度量时空变化程度[34]。

(1) 动态度 土地利用类型变化动态度 ρ为[12]：

ρ=1T∑ijnΔA(i, j)A(i)(2)

式中, T为时间段, ΔA(i, j) 为监测开始至监测结束时段内第i类土地利用类型转换为第j类土地利用类型面积总和, A(i) 为监测开始时间第i类土地利用类型总面积, 土地利用动态度 ρ反映与T时段对应研究区土地利用变化速率, n为土地利用类型数。显然, 第i类土地利用类型动态度为：

ρi=1T∑jnΔA(i, j)A(i)(3)

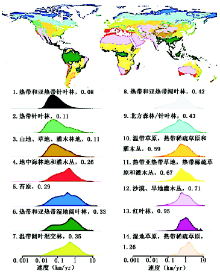
(2) 时空速度 物种的生存可能取决于适应变动的气候, 包括在时间和空间两个方面的气候变动, 据此构造[13]：

温度变化时空速度(km/year)=温度空间梯度(oC/km)温度时间变率(oC/year)(4)

其物理含义是为保持温度不变所需要的沿地球表面的瞬间局部速度。图10上为温度变化时空速度分布, 下图是按生物群系统计的时空速度直方图。所用数据是A1B排放情景全球格网2000-2100逐年。全球平均0.42 km/year, 热带针叶林0.08 km/year, 对气候变化最为敏感; 洪泛草地1.26 km/year, 对气候变化最不敏感。

图10全球温度时空变化速度分布及其按生物群系直方图[13]Fig. 10 The velocity of temperature change by biome[13]

读者可以根据在研问题构造自己的具有物理机制的“ 变化指标” , 有针对性地深刻地揭示再研问题的时空变化机制。

4.4 时空格局和异常探测

时空格局是指事物属性的时空规律性, 能够被人类智力理解、掌握和预测。中国近3000个县级行政单元, 每个空间单元格中的值 (如GDP、温度等) 都随时间变化, 组成高维数据, 超出人脑处理能力。时空格局分析工具将时空变化信息压缩降维, 以二维平面图表达, 反映时空格局。与时空格局相关的概念是景观格局, 后者是指大小和形状各异的景观要素在空间上的排列和组合[36]。表现出规律性的景观格局可以称作时空格局。异常指时空点与其周围时空格局的差别。

(1) SOM时空聚类 自组织映射SOM (Self Organization Mapping) 将y(s, t) 数据, 分类为事先指定的数L = m× n类, 其中s, t分别表示空间点和时间点, m, n是两个正整数, 其值接近[37]。具体算法如下。每一类用一个神经元z(k, t) 表示, k = 1, 2, …, L个类型, 放置一个m× n二维平面上。第一步, 将y(s, t) 标准化为[0, 1]之间的值, 将z(k, t) 赋以[0, 1]间的随机数; 第二步, 计算距离d(s, k)

d(s, k)=∑t|y(s, t)-z(k, t)||(5)

式中, ||· ||表示距离测度, 例如, 欧几里得距离, 􀰐表示求和。第三步, 给定一个s* , 神经元k* 赢得s* , 假如min d(s* , k) (∀ k); 第四步, 对于神经元k* 及其周围, z(k* , t)τ +1 = z(k* , t)τ +a[y(s* , t)-z(k* , t)τ ], 其中a是一个事先给定的 (0, 1) 之间的学习速度; 第五步, 对于另外一个s, 到第三步, 直至∀ s; 第六步, 到第二步开始下一轮迭代, 直至τ max; 第七步, 每个s都被分类到一个类型k; 按z(k) 均值大小将L个神经元升序排列。将中国中东部1456个县市 (s = 1, 2, …, 1456) 2008年5月至2009年3月共11个月 (t = 1, 2, …, 11)手足口病和降雨分别进行SOM时空聚类, 各分16类, 可见中国中东部手足口病和降水的时空类型, 发现手足口病高发区在降雨高发区之内[38]。

(2) EOF时空分解 经验正交函数EOF (Empirical Orthogonal Function), 也称主成分分析PCA (Principal Component Analysis), 将时空数据y(s, t), 其中空间s = 1, …, N和时间t = 1, …, T, 通过坐标变换矩阵RN× N将信息即方差压缩到z(k, t), k = 1, …, N和时间t = 1, …, T中k的前几项[39]：

z=Ry(6)

式中, R是待求矩阵。使z方差最大, 得到R由y的协方差矩阵CN× N的N个特征向量r组成, RN× N: (C-λ ) R = 0。R按特征值降序排列, z的N个方差等于C的N个特征值, R的第i列即为第i个EOF, EOFs = R, PCs = yR。图11是中国手足口病的EOF和PC分解, 两个模态EOF1和EOF2已解释了原始数据中66%的信息[40], 控制了手足口病时空变异, 反映了其时空格局。

图11 中国2008年手足口病EOF时空分解[40]Fig. 11 EOF modes of HFMD in China in 2008[40]

(3) 时空热点探测 SatScan是当今有代表性的时空热点扫描技术[41], 以此为例简述时空热点探测原理。对于研究区域 R, 有时空全覆盖监测数据y(s, t), 对于某个时空点(s, t), 该时空点的期望发病人数等于整个研究区 R的平均发病率乘以该时空点人数, 该时空点实际发病人数与期望发病人数之比即为该时空点的OR值 (odd ratio); 同样地可以计算该点以外的OR值; 这两个OR值之比即为该时空点的RR值 (relative rate)。当RR值大于1, 该时空点患病风险大于其外时空。逐步扩大该时空点的时空半径, 直至覆盖研究区1/2人口, 每次计算半径内的实际RR值, 取RR值最大的半径作为潜在热点区。将研究区所有时空点的观测病例数在所有时空点上随机重新排列999次, 分别计算潜在热点区在这999次病例随机排列下的RR值, 降序排列RR值。实际RR值在降序排列RR值中的位次, 例如第5位, 即为其有别于随机排列的统计显著水平, 即0.005的显著性水平, 热点高度显著。

(4) 多维热点探测 时间— 空间— 属性多维聚集智能搜索技术[42]。将研究区域内每个病例都看成一个待聚类的对象, 首先不考虑这些病例对象的实际空间位置, 只是利用群聚类算法 (Ant-based Clustering Algorithm, ACA) 将它们根据属性投影到一个二维平面上。然后在平面上放置若干只人工蚂蚁, 每只蚂蚁能随机选择一个病例对象, 并计算该病例对象与其周边病例在多维属性值上的相似度, 以此来决定是否拾起、移动或放下该对象, 通过若干次循环迭代运算后, 蚂蚁把属性相似的病例点放在了一起, 得到了病例的属性聚类结果。最后通过判断同一属性聚类的病例点之间的空间邻近关系, 以使属性聚类又有了空间聚集性意义。利用Bayesian Gamma-Poisson模型和过去有关研究区域疫情暴发先验值来计算每个可能存在的传染病聚类成为真实暴发的后验概率以及研究区域存在传染病暴发的可能性。若研究区域内有较大的可能性发生了传染病暴发, 那么真实暴发后验概率排在前几位的病例划分就被判定为传染病高发热点区域, 并在地图上进行定位。由于前一步考虑的是病例的“ 属性— 空间” 信息, 第二步又加入病例发生地以往传染病暴发的时间信息, 所以方法得到的最终结果是传染病在“ 时间— 空间— 属性” 多维度上的聚集。

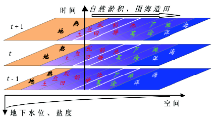
(5) 地球信息图谱 通过人脑对各种信息的直觉和综合分析与逻辑推理, 制作地球信息图谱, 揭示时空演化所遵循的规律[43]。例如, 淤积海岸带生态系统受地下水位和盐度强烈控制, 而地下水位和盐度随距海距离递减呈现有规律的条带状分布 (图12最下部坐标系)。如黄河三角洲和江苏海岸带, 受地下水位和土壤盐度空间条带状分布所控制, 其上的天然植物、养殖业、种植业的空间分布自海岸线向陆地方向自然演化, 呈条带状依次排列[44]。随着淤积海岸向海洋方向不断延伸, 可以预测, 地点s过去 (t - 1) 是芦苇地, 现在 (t) 是池塘, 按照演替规律, 未来 (t+1) 将是稻田。

图12 淤积海岸土地利用演化图谱[44]Fig. 12 Evolution of land use in alluvial coast[44]

时空格局或异常的发现, 即可以基于观测数据运用SOM、EOF、扫描和搜索等数值和智能算法, 也可以基于专家知识运用地球信息图谱思想的定性方法, 还有景观生态学关于时空格局的理论。因输入数据和知识的差异, 算法和信息综合方式不同, 时空格局的含义有区别。SOM将高维数据按照相似性聚类。如果数据中不存在分异性 (strata), SOM将消失。EOF将高维数据按照方差 (信息量) 分解为几个互相正交的的主要模态以及噪音。如果数据中不存在相关性, EOF将消失。地球信息图谱揭示时空过程的规律性, 给定地点, 可以根据图谱定性地预测其状态随时间的变化。时空热点探测通过比较与周围时空属性值的差异发现异常值, 进行预警。

4.5 时空数据插值

时空抽样数据, 可以通过时空插值技术, 得到遍历时空的数据集。例如, 中国960万km2现有700多个国家级地面气象台站, 每天进行4次观测。要获得每月全国任意一点的月平均气温值, 就需要进行时空插值。y(s, t) 记一个时空点 (s, t) 上的变量。基于统计学的方法主要有时空Kriging, BME和综合法等。这些都昰基于时空相关性[45]的单变量方法。

(1) 时空Kriging插值模型 时空Kriging是空间Kriging方法的简单推广。对时空点 (s0, t0) 的估计值 y^(s0, t0) 是该时空点周围观测值y(s, t) 的加权和。估计值, 估值方差和无偏约束分别为[3]：

y^(s0, t0)=∑w(s, t)y(s, t)(7)

v=E[y^(s0, t0)-y(s0, t0)]2→最小(8)

Ey^(s0, t0)=y(s0, t0)(9)

式中, w(s, t) 为权重, v是估值方差, E为数学期望。为求解, 需要假设y(s, t) 时空二阶平稳, 即y(s, t) 的数学期望时空处处相等, 并且两时空点(s, t) 和 (s + h, t + τ ) 之间的协方差只与时空距离有关, 与时空绝对位置无关, cov[Y(s; t), Y(s + h, t + τ )]= C(h; t), 给定指数如exp[-(h + τ )β ]或其他函数形式, 由实测样本值拟合参数。以上有约束极值问题在二阶平稳假设条件下可求得权重w(s, t), 从而得到 y^(s0, t0) 及其均方差。

(2) BME插值模型 贝叶斯最大熵BME (Bayesian Maximum Entropy) 为时空建模和插值建立了一个知识综合框架, 包括一般核心知识G-KB (包括自然法则如遗传和变异, 理论模型如SIR, 科学理论如质量守恒, 和经验关系如剂量— 反应弹性) 和特定知识S-KB (如硬数据, 不确定性)。BME包括下面两个基本方程[2, 46]：

fy(s, t)=A-1∫ξeμgdy(s, t)(10)

∫(g-g̅)eμgdy(s, t)=0(11)

式中, fy(s, t) 是属性y(s, t) 的概率密度函数; A是标准化参数; ξ 代表S-KB; g是一个向量, 其元素代表G-KB; μ 是g的权重向量, 求解该方程组得到。 g̅表示g的均值。在时空点 (s, t) 气象要素的BME平均估计及其方差分别是： y^(s, t)=∫y(s, t)fy(s, t)dy(s, t), σy(s, t)2=∫y^(s, t)-y(s, t)2fy(s, t)dy(s, t)。网络搜索BMElib即可找到BME的最新免费软件下载。

时空Kriging是线性方法, 而BME可以是线性或者非线性, 并且可以融合多种知识和多种数据, 更加符合实际。当只有采样点数据y时, 时空Kriging和BME插值结果接近, 时空Kriging比较简单易行。无论是时空kriging还是BME方法, 在用于海量数据时空估计时都面临如何减小计算量的问题。Cressie等[47]发展了一套基于数据降维来降低计算量的kriging方法, 称作FRK (Fixed Rank Kriging, 固定顺序克里格), 并将该方法扩展到时空数据, 发展了FRF (Fixed Rank Filter, 固定顺序滤波) 的方法[48, 49]。Furrer等[50]发展了CT (Covariance Tapering, 协方差锥) 算法克服海量数据kriging中的大计算量问题。

4.6 时空回归

回归的目的是寻找因变量y和自变量x的关系。实际上对经典回归或空间回归模型进行简单延伸即可得到时空回归模型。包括时空面板模型、时空BHM (Bayes Hierarchical Model)、贝叶斯网络有向无环图模型[51]、时间T-GWR (Geographical Weighting Regression)、时空GAM (Generalized Addable Model) 等等。

(1) 时空多元线性回归模型。包括被解释变量y和k个解释变量x。

y(s, t)=ρWy(s, t)+∑k=2kβkxk(s, t)+ε(s, t)(12)

式中, y, x为观测值, s, t分别表示空间位置和时间点; 参数ρ , β 为待估计参数, W为空间连接矩阵, e为回归误差。可由MLE (最大似然估计) 和 GLS (广义最小二乘) 求解[52]。

(2) 时空BHM。时空贝叶斯层次模型较难理解[20], 举例说明：令y(s, t) 表示全国各省市自治区直辖市 (s = 1, …, 34) 自2010年以来逐年 (t = 1, …, 4) H7N9新发病例数

y(s, t)~ Poisson(n(s)θ(s, t))(13)

logθ(s, t)=α+u(s)+v(t)+ϕ(s, t)+βx(s)(14)

式中：Poisson为普松概率密度函数; n(s) 为省s的病例数, θ(s, t) 为发病率, α 为中国过去4年H7N9流行率, u(s) 为随机效应以抓取H7N9发病率过去4年共同且稳定的空间格局 (可用空间自回归模型+正态分布建模), v(t) 为随机效应以抓取H7N9发病率横跨全国稳定的时间趋势 (可用一阶随机走路模型), ϕ (s, t) 为无结构随机效应项 (iid正态, 所有年份具有共同方差) 以允许时空相互作用 (特定时间方差) 和过离散, β 为回归系数, x(s) 为解释变量。求解使用基于MCMC算法的WinBUG软件和考虑空间相关性的GeoBUGS软件, 网络可搜索这两个软件名下载。

时空多元线性回归模型揭示了因变量和自变量之间的弹性关系, 解释清晰。如果时空过程存在空间异质性和时间非平稳性时, 模型 (12) 式的将扭曲因变量和自变量的关系。使用面板数据模型, 允许截距项和斜率项空间可变, 可以克服这一问题, 并且刻画更加细致的关系[52]。对于小样本, 可以通过假设参数概率分布和“ 邻居借力” 进行弥补, 这时需要使用时空BHM。BHM通过假设数据y, 过程u和v, 以及参数的概率分布还可以考虑多种不确定性, 使得估算更加准确。时空面板模型和BHM一般需要使用MCMC算法求解, 常用GeoBUG软件。

4.7 过程建模

当时空过程机理清晰和主导时, 可以据此建立时空过程的数学模型。相对于统计模型而言, 过程模型反映运动本质, 容易解释, 用于仿真和预测。不同的过程具有不同机理, 因而有不同的模型。这种不同体现在模型机理不同、或者模型形式不同、或者变量不同、或者参数不同。

(1) CA和ABM (元胞自动机和智能体模型) 地理元胞自动机CA (Cellular Automaton)[53]首先将研究区划分为格网, 一个格网的土地利用类型y(s, t) 与解释变量x(s, t) 与上一时段相同格网状态y(s, t') 和周围格网状态y(s', t') 有关, 据此构建格网状态转换规则f：

y(s, t)=f[y(s, t'), y(s', t'), x(s, t)](15)

可以是观测数据拟合多元线性回归、遗传规划、粒子群、神经网络、贪婪算法、案例推理等模型。给定初始和边界条件, CA模型运行, 空间格局随时间演化。地理ABM (Agent Based Model)[54]用计算机智能体模拟现实中的个体行为, 多智能体可以是个人、汽车、格网土地等。给个体赋予参数、个体间相互作用规则、和个体与环境关系参数。大量个体在计算机中开始运动和相互作用, 演化。CA和ABM模型可以对个体设置人们已经理解的各种个体、相互作用和环境参数, 但是有可能产生高度非线性行为, 并且大量个体相互作用使得对计算机运算能力需求巨大。

(2) 反应扩散方程 根据能量或质量守恒定律, 热量或物质扩散方程为：

∂y(s, t)∂t-β∂2y(s, t)∂s2+ay(s, t)=δ(s, t)(16)

式中, ∂y(s, t)∂t反映了温度或物质浓度随时间变化, 它与热量或物质空间扩散 ∂2y(s, t)∂s2和热或物质源y(s, t) 有关, δ (s, t) 是损耗项。Cressie[3]将此物理模型运用于地理时空模拟。适用于具有反应扩散机制的地理现象模拟, 例如大气污染物扩散。

(3) 其他时空动力学模型。区际经济CGE (Computable General Equilibrium) 模型。一个地区的经济由七个舱室组成：消费者、生产者、要素市场、商品市场、政府、储蓄与投资、和区外; 各舱室之间通过实物流和资金流所组成的社会核算表SAM联系起来, 保持流入流出平衡; 各变量之间的弹性系数用统计数据估算。由此得到该地区模型; 多个地区CGE连立起来即得到区际CGE模型, 可以用于多种经济和环境政策的时空效果模拟[55]。大气动力学GCM (General Circulation Model) 模型。大气变化遵循能量、质量、动量守恒, 据此建立了大气动力学方程组, 模拟大气的时空变化。传染病时空传播SIR模型。某区域的易感者 (Susceptible)、传染者 (Infective)、移除者 (Removed) 三个舱室在该地区及与其周围三舱室之间的相互作用是传染病时空传播的动力学机制, 据此联立各地的时间SIR方程组形成传染病时空传播模型[56]。过程建模因过程机理不同而不同, 无法通用。对于相同机理的时空过程, 地理环境空间异质性使模型的参数因地而异。在给定初始和边界条件后模型不断迭代运行, 误差可能累计, 用观测数据对模型进行同化可减少模拟误差。

4.8 时空演化树

时空数据是时空过程的产物, 因此并不是一堆杂乱无章的数字沙堆, 而人为界定在一维、二维或高维笛卡尔坐标系统, 未必能够充分地表达出演化过程。实际上, 有可能通过机理分析和观测数据反演时空过程。时空过程可能是物理的。例如, 大气动力及对应的GCM模型; 可能是经济的, 例如投入产出联系及对应的CGE模型; 可能是传染的, 例如接触传播及对应的SIR模型, 也可能是演化遗传变异的, 例如城市群演化树。

针时空演化过程所产生的时空数据, 时空演化树借鉴生物学发展演化理论, 不做维度的约束, 通过事物发展规程规律的梳理, 将多维数据中可能蕴藏的机理关联脉络和演化变异以一种简单清晰可视化的形式表达出来, 多维数据中的生命系统结构及其演化规律一览无遗[57]。

时空演化树的核心理念是：个体状态变化形成状态空间的演化路径, 多个个体的演化路径, 产生状态空间的层次结构, 用状态变量刻画。状态变量可以通过人类知识经验获取, 也可以通过统计聚类。得到群体的演化规律, 预测个体下一个状态。因此时空演化树的思路是：确定状态变量 (数据项)→ 确定状态空间 (树的结构)→ 把属性变量时空数据投影到状态空间→ 个体 (树叶) 演化路径 (树枝)→ 总结不同类型群体演化规律→ 个体状态沿着演化树的结构进行发育、成长、演化、变异, 据此可以进行状态预测和分析。不管是城市演化、地貌水系发育, 或是生物和生态系统进化, 都遵循以上规律。

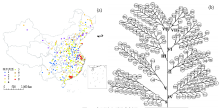
以中国城市群为例, 253个城市在地理空间上看不出太多的分布规律 (图13a)。而若将这253个城市的多元统计数据分别按城市类型和发展阶段分别聚类, 顺序地安排在一颗“ 树” 的干、支和叶上, 组成一颗城市群演化树, 我国城市群的演化规律和变异清晰可见 (图13b)。图13b每个叶子代表一个城市, 2000年共253个; 所在细枝代表同一个发展阶段的城市, 从初期的1至最高第6阶段; 8个树干表示城市类型; 越接近树根的细枝发展阶段越高。图13中的罗马字母分别表示8个城市类型, 叶子中的数字从左到右第一位表示该城市在2000年的城市类型, 第二位数字表示该城市在1990年所处的发展阶段, 第三位数字表示该城市2000年所处的发展阶段。图13中的双向箭头表示地理分布的253个城市与演化树上的253个叶子一一对应, 可互相查询检索。该树被应用于两个案例：(1) 可视化地表达各城市在国家的当前地位、发展方向和途径。(2) 解释城市化占地规律, 以此预测城市扩张, 精度较高[56]。演化树还被用于区域人群的残疾发生状况与流行病学、人口学转变的关联分析[58]、可持续发展[11]问题的研究。

图13 中国城市群演化树[57]Fig. 13 Evolution tree of cities in China[57]

时空机理方法从物理过程、影响因素和状态演化来理解和掌握时空规律, 包括过程建模、时空回归和演化树。其中演化树构建的理论依据是物理学的遍历定理：个体演化组成群体演化, 通过数据建立的群体演化规律, 个体演化将遵循群体演化所展示出来的规律性。演化树还是一种可视化手段, 也建立了属性状态空间和时空格局之间的映射关系, 反映了属性值的时空变化由量变到质变导致状态变量的时空格局。这里映射关系可以通过SOM、K-means等分类算法建立。

4.9 工具组合及其他工具

每个工具都有其长处和局限性, 单独使用犹如管中窥豹。恰当地组合使用将发挥各方法的长处, 取长补短, 形成“ 优势组合拳” , 对目标形成的完整认识。以下举例说明。

(1) BME-SOM组合 BME是插值方法, SOM是分类算法。研究手足口病与气象要素的关系, 前者以县级行政单元记录每周数据, 后者以全国700多个国家级地面气象台站观测数据, 需要统一时空数据尺度。用BME将气象台站数据时空插值到周、县的时空格网中; 然后分别对手足口病和气象要素实施SOM降维, 分析其时空格局异同, 得到两者之间的关系[38]。

(2) 模型驱动的时空协方差矩阵 协方差矩阵是时空统计建模的基本参数, 一般由实测样本拟合给定的函数形式得到。当样本量小时, 误差较大。这一缺憾可由动力学模型克服。例如, 传染病传播的时空SEIR模型包含了多个变量的时空相互关系, 据此建立各变量的时空协方差机理关系, 再用几个观测数据即可对其进行标定, 从而建立时空协方差矩阵[55]。

(3) 多模型耦合推理[33] BW统计被用来识别北京2003年SARS在18个区县传播影响因子的时间变化[59], HC层次空间聚类获得SARS密切接触者的空间格局, 每日Moran's I的小波分解得到SARS的空间聚集的时间演化, SEIR模型模拟了SARS的时间过程。通过共同项将不同模型两两连接起来：SEIR和I通过共同时间项连接起来, SEIR与BW通过共同时间项连接起来, BW与SEIR通过共同时间项连接起来, I与HC通过空间聚集项连接起来, HC与BW通过交通因子连接起来, 从而将这四个模型的发现连接成网, 形成空间~时间~驱动力的联动推理网。

(4) 逻辑推理 新发突发事件、罕见事件、社会发展导致疾病减少、精细化的小数据分析, 都缺少重复样本, 统计学难以进行。实际上, 逻辑制约关系可以将推断限定在一定范围内。如果再有一些类似案例和背景知识, 可以进一步降低推断的不确定性。对于小概率事件, 可以用逻辑制约和推理关系在一定精度上实现推理[60]。

5 讨论和结论
5.1 讨论

1960年代北美和欧洲掀起的计量地理革命的种子, 与1980年代趋于实用的GIS技术和增强的空间数据获取能力结合, 到1980年代产生了空间统计学并不断发展。现在, 空间插值Kriging, 空间相关性检验Moran's I, 空间热点探测LISA, 空间回归, 地理加权回归GWR, Bayes空间多水平建模, 空间扫描统计SatScan、地理探测器等方法已经被普遍使用[20, 21, 22, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71], 为空间数据分析提供了有力工具。

一个粒子运动存在3个自由度, 即上下、左右、前后, 按照牛顿力学方法, 确定它的运动方向, 就可以计算它的运动速度、轨迹等。但如果是大量的粒子, 加在一起会有无法计算的自由度量, 无法计算出它们全体总的运动效果, 只能用统计方法计算, 即概率论和数理统计的方法计算。类似地, 统计学也是时空数据和时空大数据分析的基础。

大数据信息量巨大, 需要归纳总结, 也就是统计, 才能被人脑掌握。时空大数据为事件发现和统计推断提供了大样本, 符合统计学大数定律, 更加适合统计学的使用条件。同时, 由于时空大数据多是方便采样、选择性采样、非重复抽样和样本质量无控, 这对基于随机样本的统计学方法提出挑战, 从而对基于统计学的时空数据方法提出了挑战。

(1) 微博、网络、手机、浮动车等大数据 (样本) 的生成者通常并不是全体人群 (总体), 也不是总体的随机样本, 因此样本有偏于总体, 用有偏样本推断总体时需要纠偏[72, 73], 结合大数据类型进行纠偏是一个值得研究的关键科学问题。

(2) 大数据质量参差不齐, 是用全体数据进行统计推断, 还是基于其中一部分质量好的子样本进行统计推断, 以达到无偏最优推断的目的, 子样本量的选取存在临界点, 这是大数据理论中值得研究的另一个关键问题。

(3) 由于样本量增加, 直接使用大数据辅以统计学方法和机器学习方法可以增加事件发现的灵敏度, 减少漏报率, 减少统计学第一类错误; 同时, 由于样本质量无控, 虚报率将增加, 增加统计学第二类错误, 统计推断的置信区间也将变宽。因此, 大数据分析需要大智慧, 空间抽样和统计推断将是时空大数据分析的核心方法之一。另一方面, 空间抽样与统计推断方法本身也需要进一步发展以更好地适应大数据特点, 以准确地挖掘出大数据中的信息。

时空数据分析对象是地学, 方法是统计学。由于地学对象的多样性和复杂性, 数学和统计学理论的单纯性和准确性, 两者结合不可能一蹴而就。数学基础好的地理学家 (例如Luc Anselin, Robert Haining, Manfred Fischer, George Christakos, Arthur Getis, Stewart Fotheringham, Micheal Goodchild) 和对地学有兴趣的统计学家 (例如Julian Besag, Patrick Moran, George Matheron, Noel Cressie), 或者两个学科的合作 (例如地理学家A.D. Cliff 和统计学家J.K. Ord), 经过近半个世纪的努力, 发展建立了空间统计学。国内外学者以此为理论基础, 以近年大量的时空数据分析实践和需求为牵引, 正在创新和发展时空统计方法及理论体系。

5.2 结论

随着时空数据的积累和大数据时代的到来, 有大量的时空数据分析挖掘工作。工欲善其事, 必先利其器, 需要对已有的时空数据分析方法做系统的归纳总结形成工具箱, 并且研发新的工具。按照使用目的的不同, 时空数据分析主要包括可视化工具集、变化统计工具集、插值与格局识别工具集、以及机理建模工具集等四大类。前三类是单变量方法, 时空机理工具是多变量方法。不同的方法不是完全独立割裂的, 有时可以同时或组合使用。例如, 时空机理工具集是为了建立因变量和自变量之间的关系, 也可以用于空间插值。变化探测工具是为了度量时空变化, 也可以作为其他时空分析的先导。

致谢：张志宏修改了文中的图件。评审人的意见使本文得到改进。

The authors have declared that no competing interests exist.

参考文献
[1] Li X, Cheng G D, Liu S M, et al. Heihe Watershed Allied Telemetry Experimental Research (HiWATER). Bulletin of American Meteorological Society, 2013, 94(8): 101175/BAMS-D-12-00154. [本文引用:1] [JCR: 6.591]
[2] Christakos G. Modern Spatiotemporal Geostatistics. Oxford: Oxford University Press, 2000. [本文引用:4]
[3] Cressie N, Wikle C K. Statistics for Spatio-Temporal Data. Wiley, 2011. [本文引用:6] [JCR: 4.186]
[4] Sherman M. Spatial Statistics and Spatio-Temporal Data: Covariance Function and Directional Properties. Wiley, 2011. [本文引用:1] [JCR: 4.186]
[5] Cai Yunlong, Lu Dadao, Zhou Yixing, et al. Chinese progress and international trends of geography. Acta Geographica Sinica, 2004, 59(6): 803-810.
[蔡运龙, 陆大道, 周一星等. 地理科学的中国进展与国际趋势. 地理学报, 2004, 59(6): 803-810. ] [本文引用:1] [CJCR: 2.937]
[6] Wang Zheng, Xia Haibin, Wu Jing. GeneralGeography. Beijing: Science Press, 2010.
[王铮, 夏海斌, 吴静. 普通地理学. 北京: 科学出版社, 2010. ] [本文引用:1]
[7] Gu Chaolin. An Introduction to Human Geography. Beijing: Science Press, 2012.
[顾朝林. 人文地理学导论. 北京: 科学出版社, 2012. ] [本文引用:1]
[8] Zhang Hui. Spatio -temporal variations of population and population distribution with data at county level in Northwest China in 1990-2010 Journal of Arid Land Resources and Environment, 2013, 27: 33-39.
[张慧. 1990-2010年西北地区县域人口数量与空间集疏变化时空分析. 干旱区资源与环境, 2013, 27: 33-39. ] [本文引用:1] [CJCR: 0.861]
[9] Wang Xingfeng, Wang Yunjia. Analysis and assessment model of environmental cumulative effects based on the integration of SD, CA and GIS methods and its application. Acta Scientiae Circumstantiae, 2013, 33(7): 2078-2086.
[王行风, 汪云甲. 基于SD-CA-GIS 的环境累积效应时空分析模型及应用. 环境科学学报, 2013, 33(7): 2078-2086. ] [本文引用:1] [CJCR: 1.689]
[10] Luo Chengfeng, Xu Changjun, You Haoyan, et al. Analysis on grassland degradation in Qinghai Lake Basin during 2000-2010 Acta Ecologica Sinica, 2013, 33(14): 4450-4459.
[骆成凤, 许长军, 游浩妍等. 2000-2010年青海湖流域草地退化状况时空分析. 生态学报, 2013, 33(14): 4450-4459. ] [本文引用:1]
[11] Zhang Wei, Duan Xuejun, Zhang Weiyang. Evaluation and evolution of sustainable development in Yangtze River Delta. Resources and Environment in the Yangtze Basin, 2013, 22(10): 1243-1249.
[张伟, 段学军, 张维阳. 长三角地区可持续发展测度与演化分析. 长江流域资源与环境, 2013, 22(10): 1243-1249. ] [本文引用:2] [CJCR: 1.536]
[12] Liu Jiyuan, Kuang Wenhui, Zhang Zengxiang, et al. Spatial patterns and driving forces of land use change in China in the early 21st century. Acta Geographica Sinica, 2014, 69(1): 3-14.
[刘纪远, 匡文慧, 张增祥等. 20世纪80年代末以来中国土地利用变化的基本特征与空间格局. 地理学报, 2014, 69(1): 3-14. ] [本文引用:2] [CJCR: 2.937]
[13] Loarie S R, Duffy P B, Hamilton H, et al. The velocity of climate change. Nature, 2009, 462: 1052-1055. [本文引用:2] [JCR: 38.597]
[14] Li A, Bo Y, Zhu Y, et al. Blending multi-resolution satellite sea surface temperature (SST) products using Bayesian maximum entropy method. Remote Sensing of Environment, 2013, 135: 52-63. [本文引用:1] [JCR: 5.103]
[15] Chalmond B. Spatio-temporal graphical modeling with innovations based on multi-scale diffusion kernel. Spatial Statistics, 2014, 7: 40-61. [本文引用:1]
[16] Diaz-Avalos C, Mateu P J J. Significance tests for covariate-dependent trends in inhomogeneous spatio-temporal point processes. Stoch Environ Res Risk Assess, 2014, 28: 593-609. [本文引用:1]
[17] Wang J F, Xu C D, Hu M G, et al. A new estimate of the China temperature anomaly series and uncertainty assessment in 1900-2006. Journal of Geophysical Research: Atmospheres, 2014, 119(1): 1-9. [本文引用:1]
[18] Wang J F, Stein A, Gao B B, et al. A review of spatial sampling. Spatial Statistics, 2012, 2(1): 1-14. [本文引用:3]
[19] Goodchild M M. Prospects for a space-time GIS. Annals of the Association of American Geographers, 2013, 103(5): 1072-1077. [本文引用:1]
[20] Haining R. Spatial Data Analysis: Theory and Practice. UK: Cambridge University Press, 2003. [本文引用:3]
[21] Wang Jinfeng. SpatialAnalysis. Beijing: Science Press, 2006.
[王劲峰. 空间分析. 北京: 科学出版社, 2006. ] [本文引用:3]
[22] Fischer MM, Getis A. Hand book of Applied Spatial Analysis. Berlin: Springer, 2010. [本文引用:3]
[23] Wang J F, Liu X, Christakos G, et al. Assessing local determinants of neural tube defects in the Heshun Region, China. BMC Public Health, 2010, 10: 52. [本文引用:1] [JCR: 2.076]
[24] Wu J L, Wang J F, Meng B, et al. Exploratory spatial data analysis for the identification of risk factors to birth defects. BMC Public Health, 2004, 4: 23. [本文引用:1] [JCR: 2.076]
[25] MacEachren A. How Maps Work: Representation, Visualization, and Design. New York: Guilford Press, 1995. [本文引用:1]
[26] Hägerstrand T. What about people in regional science? Papers of the Regional Science Association, 1970, 24: 1-12. [本文引用:1]
[27] Shaw S L. Fleming Lecture, AAG Meeting. 2009. [本文引用:1]
[28] Wang J F, Wang Y, Zhang J, et al. Spatiotemporal transmission and determinants of typhoid and paratyphoid fever in Hongta District, China. PLoS Neglected Tropical Diseases, 2013, 7(3): e2112. [本文引用:1] [JCR: 4.569]
[29] Zheng Xinqi, Wang Jiayao, Yan Hongwen, et al. Design and application of digital land price model for land price evolvement in urban area. Resources Science, 2004, 26(1): 14-21.
[郑新奇, 王家耀, 阎弘文等. 数字地价模型在城市地价时空分析中的应用. 资源科学, 2004, 26(1): 14-21. ] [本文引用:1] [CJCR: 2.123]
[30] Sulçe A, Drate P, Costa A C, et al. Space-time patterns of temperature in Sweden and Europe. Multidisciplinary research on geographical information in Europe and beyond. Proceedings of the AGILE'2012 International Conference on Geographic Information Science, Avignon, April 24-27, 2012. [本文引用:1]
[31] Lin H, Chen M, Lu G N, et al. Virtual geographic environments (VGEs): A new generation of geographic analysis tool. Earth-Science Reviews, 2013, 126: 74-84. [本文引用:1] [JCR: 7.339]
[32] Pei T, Zhou C H, Zhu A X, et al. Windowed nearest-neighbour method for mining spatio-temporal clusters in the presence of noise. International Journal of Geographical Information Science, 2010, 24(6): 925-948. [本文引用:1] [JCR: 1.613]
[33] Wang JF, Christakos G, Han WG & Meng B. Data-driven exploration of 'spatial pattern-time process-driving forces' associations of SARS epidemic in Beijing, China. Journal of Public Health, 2008, 30(3): 234-244. [本文引用:2] [JCR: 1.993]
[34] Wang J F, Xu C D, Tong S L, et al. Spatial dynamic pattern of hand -foot-mouth disease in China. Geospatial Health, 2013, 7(2): 381-390. [本文引用:2] [JCR: 1.648]
[35] Kwan MP. Space-time and integral measures of individual accessibility: A comparative analysis using a point-based framework. Geographical Analysis, 1998, 30(3): 191-216. [本文引用:1]
[36] Fu Bojie, Chen Liding, Ma Keming, et al. Principle and Application of Land scape Ecology. 2nd ed. Beijing: Science Press, 2011.
[傅伯杰, 陈立顶, 马克明等. 景观生态学原理及应用. 2版. 北京: 科学出版社, 2011. ] [本文引用:1]
[37] Kohonen T. Self-OrganizingMaps, Springer-Verlag: Berlin, 2001. [本文引用:1]
[38] Wang J F, Guo Y S, Christakos , et al. Hand , foot and mouth disease: spatiotemporal transmission and climate. International Journal of Health Geographics, 2011, 10: 25. [本文引用:2]
[39] Lorenz E N. Empirical Orthogonal Function and Statistical Weather Prediction. Statistical Forecasting Project Scientific Report No. 1. MIT, 1956. [本文引用:1]
[40] Shi R X, Wang J F, Xu C D, et al. Spatiotemporal pattern of hand -foot-mouth disease in China: An analysis of empirical orthogonal functions. Public Health, 2014, 128: 367-375. [本文引用:1] [JCR: 1.35]
[41] Kulldorff M. A spatial scan statistic, communications in statistics: Theory and Methods, 1997, 26: 1481-1496. [本文引用:1] [JCR: 0.298]
[42] Liao Yilan, Wang Jinfeng, Yang Weizhong, et al. A study on detecting multi-dimensional clusters of infectious disease. Acta Geographica Sinica, 2012, 67(4): 435-443.
[廖一兰, 王劲峰, 杨维中等. 传染病多维度聚集性探测方法. 地理学报, 2012, 67(4): 435-443. ] [本文引用:1] [CJCR: 2.937]
[43] Chen Shupeng. Research on Geo-information Atlas. Beijing: The Commercial Press, 2001.
[陈述彭. 地球信息图谱探索研究. 北京: 商务印书馆, 2001. ] [本文引用:1]
[44] Wang Jinfeng. Qualitative and quantitative analysis of map. Journal of Geo-information Science, 2009, 11(2): 169-175.
[王劲峰. 地图的定性和定量分析. 地球信息科学学报, 2009, 11(2): 169-175. ] [本文引用:1]
[45] Li Xiaowen, Cao Chunxiang. The first law of geography and spatial-temporal proximity. Nature Magazine, 2007, 29(2): 69-71.
[李小文, 曹春香. 地理学第一定律与时空邻近度的提出. 自然杂志, 2007, 29(2): 69-71. ] [本文引用:1]
[46] Christakos G, Bogaert P, Serre M L. Temporal GIS. Berlin: Springer-Verlag, 2002. [本文引用:1]
[47] Cressie N and Johannesson G. Fixed rank kriging for very large spatial data sets. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 2008, 70(1): 209-226. [本文引用:1]
[48] Cressie N, Shi T. Fixed rank filtering for spatio-temporal data. Journal of Computational and Graphical Statistics, 2010, 19(3): 724-745. [本文引用:1] [JCR: 1.269]
[49] Kang L, Cressie N, Shi T. Using temporal variability to improve spatial mapping with application to satellite data. Canadian Journal of Statistics, 2010, 38(2): 271-289. [本文引用:1] [JCR: 0.591]
[50] Furrer R, Genton M G, Nychka D. Covariance tapering for interpolation of large spatial datasets. Journal of Computational and Graphical Statistics, 2006, 15(3): 502-523. [本文引用:1] [JCR: 1.269]
[51] Li L F, Wang J F, Leung H, et al. A Bayesian method to mine spatial datasets to evaluate the vulnerability of human beings to catastrophic risk. Risk Analysis, 2012, 32(6): 1072-1092. [本文引用:1] [JCR: 2.278]
[52] Gujiarati. Basic Econometrics. 4th ed. McGraw-Hill Company, 2004. [本文引用:2]
[53] Li Xia, Liu Xiaoping. Case-based cellular automaton for simulating urban development in a large complex region. Acta Geographica Sinica, 2007, 62(10): 1097-1109.
[黎夏, 刘小平. 基于案例推理的元胞自动机及大区域城市演变模拟. 地理学报, 2007, 62(10): 1097-1109. ] [本文引用:1] [CJCR: 2.937]
[54] Gong Jianhua, Lin Hui. Virtual Geographic Environments. Beijing: Higher Education Press, 2001.
[龚建华, 林珲. 虚拟地理环境: 在线虚拟现实的地理学透视. 北京: 高等教育出版社, 2001. ] [本文引用:1]
[55] Zhao Yong, Wang Jinfeng. CGE Model and Its Applications in Economic Analysis. Beijing: China Economy Press, 2008.
[赵永, 王劲峰. 经济分析CGE模型与应用. 北京: 中国经济出版社, 2008. ] [本文引用:2]
[56] Kolovos A, et al. Model-driven development of covariance for spatiotemporal environmental health assessment. Environmental Monitoring and Assessment, 2013, 185: 815-831. [本文引用:2] [JCR: 1.592]
[57] Wang J F, Liu X H, Peng L, et al. Cities evolution tree and its application in land occupation prediction. Population and Environment, 2012, 33: 186-201. [本文引用:1]
[58] Liao Y L, Wang J F, Chen G, et al. Clustering of disability caused by unintentional injury amongst the population aged from 15-60 years: A challenge in rapidly developing China. Geospatial Health, 2013, 8(1): 13-22. [本文引用:1] [JCR: 1.648]
[59] Meng B, Wang J F, Liu J Y, et al. Understand ing the spatial diffusion process of SARS in Beijing. Public Health, 2005, 119: 1080-1087. [本文引用:1] [JCR: 1.35]
[60] Christakos G, Wang J F, Wu J P. Stochastic Medical Reasoning and Environmental Health Exposure. London: Imperial College Press, 2014. [本文引用:1]
[61] Matheron G. Principles of geostatistics. Economic Geology, 1963, 58: 1246-1266. [本文引用:1] [JCR: 2.493]
[62] Tang Guoan, Yang Xin. ARCGIS GIS Spatial Analysis and Experiment Course. Beijing: Science Press, 2006.
[汤国安, 杨昕. ARCGIS地理信息系统空间分析实验教程 . 北京: 科学出版社, 2006. ] [本文引用:1]
[63] Zhou Xiaonong. Spatial Epidemiology. Beijing: Science Press, 2009.
[周晓农. 空间流行病学 . 北京: 科学出版社, 2009. ] [本文引用:1]
[64] Jiao L M, Liu Y L, Zou B. Self-organizing dual clustering considering spatial analysis and hybrid distance measures. Science in China-Earth Science, 2011, 54(8): 1268-1278. [本文引用:1]
[65] Zhou Chenghu, Pei Tao. Principles of GIS Spatial Analysis. Beijing: Science Press, 2011.
[周成虎, 裴韬. 地理信息系统空间分析原理. 北京: 科学出版社, 2011. ] [本文引用:1]
[66] Chen Yanguang. Mathematical methods for Geography: Foundations and Applications. Beijing: Science Press, 2011.
[陈彦光. 地理数学方法: 基础和应用. 北京: 科学出版社, 2011. ] [本文引用:1]
[67] Yan Qingwu. Spatial Data Analysis Methods Used in the Spatial Distribution of Population. Nanjing: Publishing House of Southeast University, 2011.
[闫庆武. 空间数据分析方法在人口数据空间化中的运用. 南京: 东南大学出版社, 2011. ] [本文引用:1]
[68] Hu M G, Jia L, Wang J F, et al. Spatial and temporal characteristics of particulate matter in Beijing, China with empirical mode decomposition method. Science of the Total Environment, 2013, 458-460: 70-80. [本文引用:1] [JCR: 3.258]
[69] Lucia P, Gelfand A E. Spatio-temporal modeling for real-time ozone forecasting. Spatial Statistics, 2013, 4: 79-93. [本文引用:1]
[70] Cliff A, Ord J K. Spatial Processes: Models & Applications. London: Pion, 1981. [本文引用:1]
[71] Wang Jinfeng, Li Lianfa, Ge Yong, et al. A theoretical framework for spatial analysis. Acta Geographica Sinica, 2000, 55(1): 92-103
[王劲峰, 李连发, 葛咏等, 地理信息空间分析的理论体系探讨. 地理学报, 2000, 55(1): 92-103. ] [本文引用:1] [CJCR: 2.937]
[72] Wang J F, Reis B Y. Area disease estimation based on sentinel hospital records. PLoS ONE, 2011, 6(8): e23428. [本文引用:1] [JCR: 3.73]
[73] Wang J F, Hu M G, Xu C D, et al. Estimation of citywide air pollution in Beijing. PLoS ONE, 2013, 8(1): e53400. [本文引用:1] [JCR: 3.73]