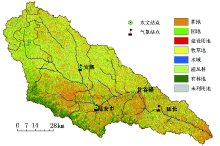
延河发源于陕西靖边县姬家畔附近的白于山东坡, 自西北向东南流经志丹、安塞、延安、延长等县 (市), 于延长县凉水岸汇入黄河, 属于黄河一级支流, 全长286.9 km, 流域面积7725 km²。延河流域, 其北部是清涧河流域、西南部为北洛河流域、南部和云岩河流域相接, 海拔最高为1731 m, 宝塔区平均海拔为958 m, 属黄土丘陵沟壑区。年降水量偏少, 年降水量在400~550 mm, 多年平均降水量为520 mm, 本地区年均气温为8.8~10.2 ^oC, 由西北向东南递增, 平均日温差13.2 ^oC。光能资源丰富, 年总辐射量为125~134千卡/cm², 有效辐射量为67.8千卡/cm²。无霜期为157~187天。延河流域残存的天然林不多, 森林草原为地带性植被, 但是, 少量的灌丛林也呈块状分布, 从而形成以牧草为主的景观现状, 干旱草本植物是植被的优势种。延河水系为延安地区第二大水系, 主要支流包括了杏子河、平桥川、西川河、南川河、蟠龙川等^{[14, 15]}。延河可以分成上、中、下游三段, 可以将流域相应划分为上、中、下游三段区域：上、中游的分界是安塞县的化子坪; 中、下游的分界是宝塔区的甘谷驿。根据中国土地利用现状分类系统, 结合研究区土地利用现状及其特点, 将土地利用类型共分为8个一级土地类型 (图1), 即：耕地 (旱地和水田)、灌丛林地、有林地、牧草地 (天然草地和人工草地)、建筑用地 (居民点、工矿及城镇用地)、园地 (果园、菜园)、水域 (河流、水库和池塘等)、和未利用地 (沼泽和滩涂地)。

图1

Fig. 1

	Figure Option ViewDownloadNew Window
	图1 延河流域2010年土地利用图Fig. 1 Land use map of the Yanhe River basin in 2010

本文主要参考延安市地理志^[14]等地理和历史文本文献^[15], 数字高程数据DEM、统计数据, 2010年土壤类型图、地形图、地貌图以及交通图、行政图等相关图件, 野外实地考察获得的植被、水文、土壤分布、土地利用和退耕还林实施情况等资料; 1956-2011年逐月实测气象数据和1990-2010年水文站点的实测水文数据; 本研究中选用的影像资料包括Landsat TM、Landsat ETM+和SPOT4 卫星遥感数据。其中, 2010年为SPOT4数据, 共9景, 空间分辨率为20 m。运用ERDAS 9.2 软件, 对2010年SPOT影像进行解译, 得到1:5万的延河流域土地利用类型空间分布图和土地利用类型的属性数据库。

SWAT模型是由美国农业部的农业研究中心研发的, 是免费、开源的, 是一种基于GIS基础之上的分布式流域水文模型, 在调参、径流模拟、地表水、非点源污染计算、面源污染、数据构建、生态修复、作物生长、参数率定、敏感性分析、农业管理措施等方面都有着广泛的应用。

SWAT模型主要的运行步骤如下：(1) 划分子流域。当流域内不同区域的土地利用或土壤属性等差异明显足以影响水文过程时, 在模拟中就需划分子流域。各子流域的输入有：气候、HRUs、坑塘/湿地, 地下水及子流域排水的主河道或河段^[16]。(2) 确定水文响应单元。水文响应单元 (hydrologic response units, HRUs) 是具有相同的植被类型、土壤条件的陆面表面综合体^[16]。水文响应单元在子流域内呈块状分布, 包含有唯一的土地覆盖、土壤和管理措施^[16]。水文响应单元 (HRUs) 体现植被覆盖类型、土壤属性和地形等信息, 这就要求输入流域的土地利用类型、土壤类型属性及地形数据。SWAT模型单独计算每个HRU的径流量, 进行汇流验算, 最后求得出口断面的流量, 从而提高模拟的精度, 可以更好地反映本流域的水量平衡。(3) 输入气象要素。划分出HRUs后, 模型的SWAT View可以为每一个HRU输入用于水文计算的气象数据, 每一个HRU的气象数据是由最近站点的气象资料赋予的^[16]。(4) 构建数据库及数据库的调整。完成以上输入工作后, 水文计算就全由模型自动完成了。(5) 模型运行。最后一步是选择合适的计算方法及输出项后执行模型运行的命令, 输出结果^[16]。

景观指数可分为斑块水平 (Patch-Metric)、景观类型水平 (Class-Metric) 和景观水平 (Landscape-Metric) 等类型, 本文应用景观格局分析软件FRAGSTATS4.1来计算景观指数。因此, 对所获得景观指数进一步做主成分分析。确定选取的景观指数共有7个, 即“ 独立核心斑块密度指数DCAD、回旋半径指数GYRATE_SD、整体性 (斑块凝聚度) 指数COHESION; 香农均匀度指数SHEI、核心斑块总面积TCA、周长面积分维指数PAFRAC、散布与并列指数IJI” 。具体景观指数表达式参见参考文献^{[17, 18]}。

本研究依据水文响应单元的三个特性：土地利用类型、土壤类型、坡度, 给每一个水文响应单元的“ 源” 、“ 汇” 景观特型赋值。

3.3.1 土地利用类型权重的确定 植被覆盖与管理因子 (C值) 区别土地利用类型。某一单元上某一种土地利用类型可能即是水土流失的源, 也是水土流失的汇, 但源和汇的贡献率不同, 例如, 林地可能汇的贡献大, 耕地源的特征很明显。本研究中土地利用类型借鉴了土壤侵蚀通用方程中的植被覆盖与管理因子(C值)^{[21, 22]}对其“ 源” 和“ 汇” 的贡献权重进行了简单赋值。确定权重的方法很多, 本研究采用专家咨询法, 并结合经验权数法和层次分析法进行修正, 对各个类型赋值。源的指数依次为：建设用地 (1.0)、耕地 (0.8)、园地 (0.6)、有林地 (0.2)、灌丛地 (0.3)、草地 (0.4)、未利用地 (0.5)、水域 (0); 汇的指数：建设用地 (0)、耕地 (0.2)、园地 (0.4)、林地 (0.8)、灌丛地 (0.7)、草地 (0.6)、未利用地 (0.5)、水域 (1)。各指数采用无量化。

3.3.2 土壤影响定量化 在本文中, 结合流域侵蚀强烈的水文过程特点, 将土壤可蚀性K值作为土壤类型的表征指标。K值越大, 抗水蚀能力越小; 反之, K值越小, 抗水蚀能力越强^[23]。为了反映土壤可蚀性K值在地块源属性和汇属性中的不同意义, 用下面公式 (1) 求得K_源和K_汇, 反映同一地块作为源和汇时其土壤的不同作用效果。

K源=1+K-K̅K̅K汇=1-K-K̅K̅(1)

式中：K_源和K_汇分别是源和汇时其土壤侵蚀能力; K为土壤可蚀性因子。

3.3.3 地形因子定量化 地形因子是影响土壤侵蚀的主要因素之一, 同时也是进行水土流失评价和土壤侵蚀预测计算的重要因子。黄土地貌则是通过其形态、结构和类型影响着侵蚀过程、方式及强度。

3.3.4 水文响应单元水土流失权重 综合上述分析, 将植被覆盖与管理因子C值、土壤可蚀性K值和坡度三者综合, 得到了水文响应单元水土流失权重 (P), 公式如下：

P源=C源×K源×sina(2)

P汇=C汇×K汇×cos a(3)

式中：C_源和C_汇分别为源和汇的植被覆盖与管理因子, 取值0~1之间^{[21, 22]}, K为土壤可蚀性值。a为水文响应单元所在坡度, sina取值介于0~1之间, cosa介于1~0之间。

本文尝试建立了小流域的“ 地形— 水文响应单元 (Slope-HRU) 景观指数” , 并确定了相关的基本概念和计算模型。对于研究区域中每一个子流域来说, 本文建立的“ 地形— 水文响应单元 (Slope-HRU) 景观指数” 就是每一个由土地利用、土壤类型和坡度要素共同确定的水文响应单元, 经水土流失“ 源” 、“ 汇” 景观权重赋值后, 作为“ 源” 和“ 汇” 的水文响应单元的累计面积比值。即Slope-HRU景观指数表示以水文响应单元为景观单元, 相对于某一坡度 (slope) 而建立的“ 源— 汇” 景观指数, 分别用源景观单元的面积和源景观的权重相乘得到的积的总和与汇景观单元的面积和汇景观的权重相乘得到的总和相比, 所得到的比值。可以用公式表示为：

R=N/M M=∑SiP源iN=∑SiP源i(4)

式中：R为Slope-HRU景观指数的值, N是汇景观加权面积总和; M是源景观加权面积总和; S_i为第i个水文响应景观单元的面积, P_源i为第i个水文响应景观单元水土流失源的权重; P_汇i为第i个水文响应景观单元水土流失汇的权重;

Slope-HRU指数计算步骤为: 首先将子流域的“ 源— 汇” 景观类型进行栅格化处理, 然后确定水文响应单元的面积和所属土壤类型及其土壤侵蚀k值、植被覆盖与管理因子C值, 所在地平均坡度, 并计算其分别作为源景观和汇景观的权重, 并依据公式4求得加权景观单元面积之和。最后用所得到的汇景观加权面积总和N与源景观加权面积总和M相除, 所得的值R即为Slope-HRU指数值。

本研究根据延河流域地形、土壤、土地利用和水土流失的实际情况, 水文响应单元定义的具体过程中, 分别将延河流域分辨率为30 m的土地利用/覆盖数据和土壤数据导入模型, 参数选取结果如下：(1) 主要参数设定：土地利用图层、土壤类型图层和坡度图层的面积比例阈值设定为, 土地利用类型数据最小面积比例为5%, 土壤类型数据最小面积比例为30%, 坡度最小面积比例为5%。(2) 坡度划分：采用Multiple Slope方法, 将坡度分为3级 (坡度按百分比), 设置坡度系数：“ slope class 1” 为0~10%、“ slope class 2” 为10%~30%、“ slope class 3” 是大于30%。将坡度如此划分的依据是：延河流域地表破碎, 沟壑纵横, 广泛分布梁、峁斜坡和沟谷陡崖, 前者坡度多在10~35度之间, 后者坡度多大于35度。这些陡坡为流水侵蚀和重力侵蚀提供了有利的地貌条件。

水文响应单元 (HRUs) 的命名规则为“ 子流域编码+土地利用/覆被类型编码+土壤类型编码+坡度 (所在区间)” , 例如：“ 18_FRST_FLc_10~30” 是指“ 第18个子流域、土地利用/覆被类型为林地、土壤类型为FLc、坡度在10%~30%之间” 的同一类水文响应单元 (HRUs)。在每个子流域内, 具有相同命名的水文响应单元 (HRUs) 可以看作是景观格局性质相同的同一种类型的“ 斑块” 。子流域中具有相同命名 (即土地利用类型、土壤类型和坡度属性相同) 的斑块是SWAT模型所划分出的最小单元, 而且该类景观单元 (斑块) 在子流域内具有相同的水文过程。HRUs的优势在于其能提高子流域内负荷预测的精度。研究时为了能在一个数据集内涵盖更丰富的信息, 一般要求生成多个子流域, 每个子流域具有的HRUs数量要合适。HRUs创建过程中会产生一个报表, 报表会列出每一个子流域中HRUs的土地利用、土壤和坡度等属性。

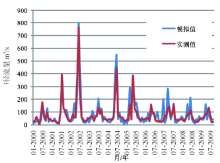
本文利用SWAT模型模拟得到延河流域逐年各月径流和产沙量。为验证结果的准确性, 将实测的资料分为两部分, 一部分用于校准模型, 而另一部分用于模型的验证。本研究方案将选择1990-2010年甘谷驿水文站的径流数据对SWAT模型进行参数率定和验证。其中选择1990-1999年为参数率定期, 而以2000-2009年的径流数据进行结果验证。模型根据径流参数的相对敏感性, 不断调整参数的取值范围, 期望得到一组合适的参数, 以求达到较好的模拟效果。1990-1999年逐月的实测日均径流量跟模拟值周期分布接近, 相关性较好 (图2和图3), 相关性系数R²为0.834; 说明模拟值与实测值接近, 且相关程度高, 可信赖。从图中可以看出, 2000-2009年的径流量模拟结果好, 与实测值的相关性和误差都在接受范围之内。相关性系数R²为0.819, 表明实测值和模拟值的相关性较高; 模拟精度高, 模拟结果可信赖。

图2

Fig. 2

	Figure Option ViewDownloadNew Window
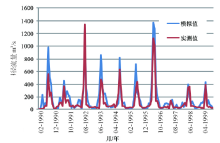	图2 1990-1999验证期逐月径流流量模拟值与实测值对比图Fig. 2 Simulated and realistic monthly runoff data in validation period from 2000 to 2009

图3

Fig. 3

	Figure Option ViewDownloadNew Window
	图3 2000-2009验证期逐月径流流量模拟值与实测值对比图Fig. 3 Simulated and realistic monthly runoff data in validation period from 2000 to 2009

本文对延河各子流域的景观指数与径流、产沙量做耦合分析。用SPSS17.0对2010年延河流域41个子流域的景观指数 (子流域水文响应单元分辨率80 m) 与年累计径流深、年产沙量进行相关分析 (表1)。全部7个所选景观指数与径流量的相关系数很小, 不能通过检验。说明前文选出的7个景观指数与延河流域的径流之间没有显著相关性。

表1

Tab. 1

表1(Tab. 1)

表1 2010年延河各子流域的景观指数与年累计径流深、年产沙量的相关系数 Tab. 1 The correlation coefficient among annual runoff, annual sediment yield and landscape index in the sub-basins of the Yanhe River basin in 2010 景观指数 独立核心 斑块密度 (DCAD) 回旋半径 (GYRATE_SD) 连通度指数 (COHESION) 香农均匀度 指数 (SHEI) 总核心面积 (TCA) 周长— 面积 分形维数 (PAFRAC) 散布与并列 指数 (IJI) 径流深 -0.127 0.057 0.156 -0.139 -0.102 -0.016 -0.288 产沙量 -0.502* * 0.335* 0.428* * 0.340* -0.186 -0.397* 0.233 * * . 在 0.01 水平 (双侧) 上显著相关。* . 在 0.05 水平 (双侧) 上显著相关。

表1 2010年延河各子流域的景观指数与年累计径流深、年产沙量的相关系数 Tab. 1 The correlation coefficient among annual runoff, annual sediment yield and landscape index in the sub-basins of the Yanhe River basin in 2010

但是, 延河流域除了TCA和IJI外其他五个景观指数与产沙量之间有一定相关性, 或者说在一定水平上有显著相关性, 五个水文响应单元景观指数与子流域产沙量数据之间有较为明显的耦合关系。具体来看, 延河流域水文响应单元景观指数与子流域产沙量之间的关系是：独立核心斑块密度 (DCAD) 与其呈显著负相关, 连通度指数 (COHESION) 呈显著正相关, 周长— 面积分形维数(PAFRAC) 与子流域产沙量呈负相关, 香农均匀度指数 (SHEI) 呈正相关, 回旋半径 (GYRATE_SD) 也呈正相关。但是, 以上各景观指数的绝对值都比较小, 在0.3~0.5左右。计算结果也说明水文响应单元总核心面积 (TCA) 和散布与并列指数 (IJI) 与各子流域的径流量和产沙量之间没有耦合关系。可以确信水文响应单元的连通性越好、多样性越高且分布越均匀土壤侵蚀越容易发生, 产沙量越大; 而且水文响应单元的密度和形状对产沙过程有影响。水文响应单元的周边越简单产沙量越大, 边界越曲折对侵蚀的约束越大。

4.4.1 Slope-HRU景观指数与水土流失量的关系 以2010年所获得的延河流域各子流域的水文响应单元数据为基础数据, 利用 MATLAB 编程语言, 实现了延河41个子流域的Slope-HRU景观指数的计算。用SPSS17.0对延河41个子流域的Slope-HRU景观指数与子流域的产流量和产沙量做相关分析 (见表2)。可以看出M与N彼此显著相关, 而且M与R显著相关, 但是N与R之间并不相关。M、N、R与产流量之间没有明显相关关系, 而M、R与产沙量之间有明显相关关系, 尤其是R与产沙量之间有显著的相关性, 相关系数达到0.6。我们也做了以下计算比较：如果去除土壤可蚀性K值, 只考虑地形和土地利用影响权重, 则生成的R与产沙量之间也有显著的相关性, 但相关系数下降为0.561。显然构建景观指数时考虑土壤可蚀性很有必要。在延河流域的Slope-HRU景观格局指数与径流量和产沙量的相关系数分别为0.069、-0.6。可以看出, Slope-HRU景观指数与径流量的相关系数接近于0, 也就是说R值不能体现产流过程, 但是各子流域R值和产沙量的相关性达到显著相关, 而且其相关系数要高于上文中计算所得到的7个景观格局指数与产沙量的相关系数。说明Slope-HRU景观指数能够有效的表征流域水土流失的特征, 在空间分布上也有一定的对应关系。本研究中不同子流域的Slope-HRU景观指数与产沙量的相关性有所差异, 这与不同区域的地理特征和土地利用格局的差异有关系。

表2

Tab. 2

表2(Tab. 2)

表2 延河41个子流域Slope-HRU景观指数 (R值) 与年径流量和产沙量相关分析结果 Tab. 2 The correlation coefficient among landscape Slope-HRU indices (R-value) and annual runoff and annual sediment yield in the 41 sub-basins of the Yanhe River basin in 2010 源景观 (M) 汇景观 (N) Slope-HRU景观指数 (R) 径流量 产沙量 源景观 (M) Pearson 相关性 1 0.809* * 0.429* * -0.075 0.320* 显著性 (双侧) 0.000 0.005 0.640 0.041 N 41 41 41 41 41 汇景观 (N) Pearson 相关性 0.809* * 1 -0.072 -0.129 -0.022 显著性 (双侧) 0.000 0.656 0.420 0.890 N 41 41 41 41 41 Slope-HRU景观指数 (R) Pearson 相关性 0.429* * -0.072 1 0.069 -0.600* * 显著性 (双侧) 0.005 0.656 0.669 0.000 N 41 41 41 41 41 径流量 Pearson 相关性 -0.075 -0.129 0.069 1 -0.077 显著性 (双侧) 0.640 0.420 0.669 0.633 N 41 41 41 41 41 产沙量 Pearson 相关性 0.320* -0.022 -0.600* * -0.077 1 显著性 (双侧) 0.041 0.890 0.000 0.633 N 41 41 41 41 41 * * . 在 0.01 水平 (双侧)上显著相关。* . 在 0.05 水平 (双侧)上显著相关。

表2 延河41个子流域Slope-HRU景观指数 (R值) 与年径流量和产沙量相关分析结果 Tab. 2 The correlation coefficient among landscape Slope-HRU indices (R-value) and annual runoff and annual sediment yield in the 41 sub-basins of the Yanhe River basin in 2010

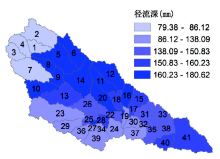
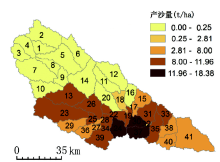
以2010年延河41个子流域的Slope-HRU景观指数和水文数据为代表, 对延河流域的Slope-HRU景观指数和水土流失状况进行了分析, 结果表明Slope-HRU景观指数和产沙状况存在明显的区域分异规律 (图4, 图5)。而且Slope-HRU景观指数R值也表现空间分异规律, 呈现由南向北, 由东向西递变的趋势。所不同的是在子流域尺度上产沙量由南向北, 由东向西递减而R值由南向北, 由东向西递增。 说明产沙量的空间变化除了受径流量作用之外还受到下垫面的地形、土壤、植被等因素影响明显, 这种影响Slope-HRU景观指数R值有所体现。但是R值最大、最小的子流域与产沙量最大、最小的子流域并不重合, 也说明R值也不能完全表征流域景观格局与水土流失过程的关系, 换句话说, Slope-HRU景观指数R值能够部分反映景观格局与水土流失过程的空间相互关系和分异规律。在第17、34子流域R值最小, 在第1、2、3、5、6、7、8、9、11、12、13、14、20子流域R值最大 (图6)。

图4

Fig. 4

	Figure Option ViewDownloadNew Window
	图4 延河流域2010年径流深空间分布图Fig. 4 Spatial distribution of runoff depth of the Yanhe River basin in 2010

图5

Fig. 5

	Figure Option ViewDownloadNew Window
	图5 延河流域2010年产沙量空间分布图Fig. 5 Spatial distribution of sediment yield of the Yanhe River basin in 2010

图6

Fig. 6

	Figure Option ViewDownloadNew Window
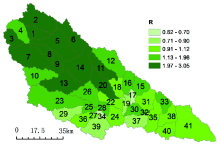	图6 延河流域41个子流域的Slope-HRU景观指数空间分布特征Fig. 6 Spatial pattern of Slope-HRU index in the 41 sub-basins of the Yanhe River basin

基于野外监测数据显示, 延河流域水土流失量存在明显的空间异质性, 呈现出自东南向西北递减的趋势, 这一趋势与本流域的年降雨量分布、地形条件、土壤可蚀性因素以及土地利用与植被覆盖之间有明显的空间变化趋势相似性, 这一趋势在Slope-HRU景观指数R值的空间分布中得到了集中体现。R值与水土流失泥沙数据呈负相关关系, 在子流域尺度上R值自东南向西北增强。水土流失严重的东南部区域R值也较小; 相对来说, 流域的西北部R值较大, 水土流失也较弱。这种空间分异特征与土地利用方式、地形和土壤类型的空间差异有必然联系。由于除了受植被、土壤类型、地形等较稳定的自然要素影响之外, 水土流失还受到降水、耕作方式、土壤管理模式 (如施肥等) 等多变因素影响, 所以, R值表现出的区域分异规律也比较复杂。总体来看, 土地覆盖、地形、土壤类型等景观要素是最重要的参数, 其空间分布格局直接影响着流域土壤侵蚀发生过程, R值是地形、土地覆盖、土壤类型等景观要素的综合量化指标, 集中表现了景观格局与水土流失过程的空间相互关系。

4.4.2 Slope-HRU的景观特征 为了进一步探索流域水文响应单元的景观格局指数, 能够更好的表现水文响应单元景观格局与产沙过程的关系, 尝试新构建的Slope-HRU景观格局指数与常用景观格局指数相结合。本文分别将选取的DCAD、GYRATE_SD、COHESION、SHEI、TCA、PAFRAC、IJI等7个常用景观格局指数与Slope-HRU景观格局指数的R值相乘, 得到独立核心斑块密度Slope-HRU景观格局指数 (DCAD-R)、回旋半径Slope-HRU景观格局指数 (GYRATE-R)、连通度Slope-HRU景观格局指数 (COHESION-R); 香农均匀度Slope-HRU景观格局指数 (SHEI-R)、核心斑块总面积Slope-HRU景观格局指数 (TCA-R)、周长面积分维Slope-HRU景观格局指数 (PAFRAC-R)、散布与并列Slope-HRU景观格局指数 (IJI-R) 等7个新综合景观指数。发现它们都与子流域的产沙量显著相关, 而且, PAFRAC-R和DCAD-R的值比Slope-HRU景观指数的R值具有更好的相关性 (见表3)。子流域的面积与周长分维数PAFRAC与Slope-HRU景观指数相结合, 二者叠加的结果放大了彼此表征生态过程的能力。水文响应单元的独立斑块密度指数DCAD与流域产沙量具有紧密的相关性, 相关系数已经达到-0.502, 比其他几个常用的景观格局指数相关性高, 再将它与Slope-HRU景观指数相结合, 二者相乘得到的DCAD-R指数, 是本文研究中找到的最具表征流域产沙过程的指数。通过分析PAFRAC-R和DCAD-R指数, 我们得到这样的结论, 也就是地形 (坡度)、土地利用、土壤类型 (可蚀性) 决定的水文响应单元的面积周长分维数和独立斑块密度能够很好的反映流域产沙情况, 均呈现负相关关系。因此, 将经过主成分分析筛选出的常用景观格局指数, 与基于水土流失的源汇理论并考虑主要景观因子而构建的源汇Slope-HRU景观指数, 二者相结合得到的综合景观指数, 具有更强的表征生态过程的能力, 其分析结果既优于常用景观格局指数也优于源汇Slope-HRU景观指数。我们再将DCAD、PAFRAC和R值三者相乘得到的积命名为独立核心斑块密度— 周长面积分维— Slope-HRU景观格局指数 (DCAD-PAFRAC-R), 经计算各子流域该指数与产沙量之间也有显著相关性, 但是相关系数与DCAD-R指数和产沙量的相关系数相同, 均为-0.626。

表3

Tab. 3

表3(Tab. 3)

表3 子流域景观格局指数与径流量和产沙量之间的相关性比较 Tab. 3 Comparison of the correlation among annual runoff and annual sediment yield and landscape indexes in the sub-basins of Yanhe River baisn 相关 系数 周长面积 分维Slope-HRU景观 格局指数 (PAFRAC-R) 独立核心 斑块密度Slope-HRU景观格局 指数 (DCAD-R) 连通度Slope-HRU景观 格局指数 (COHESION-R) 核心斑块总面积Slope-HRU景观格局指数 (TCA-R) 散布与并列Slope-HRU景观格局 指数 (IJI-R) 回旋半径Slope-HRU景观格局 指数 (GYRATE-R) 香农均匀度Slope-HRU景观格局指数 (SHEI-R) 独立核心斑块密度-周长面积分维-Slope-HRU景观 格局指数 (DCAD-PAFRAC-R) 径流量 0.067 0.025 0.083 -0.041 0.027 0.096 0.049 0.024 产沙量 -0.601* * -0.626* * -0.580* * -0.431* * -0.587* * -0.550* * -0.572* * -0.626* * * * . 在 0.01 水平 (双侧) 上显著相关。

表3 子流域景观格局指数与径流量和产沙量之间的相关性比较 Tab. 3 Comparison of the correlation among annual runoff and annual sediment yield and landscape indexes in the sub-basins of Yanhe River baisn