本文选择南京市作为研究案例地, 南京凭借其悠久的历史文化和独特的自然风光, 吸引着海内外游客, 旅游经济发展位居全国前列, 是中国著名的旅游城市。本文研究对象为城市内部旅游流动, 研究范围设定为长江以南, 南京绕城公路以内 (包括绕城公路过境) 的47个街道单元。

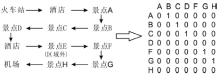
旅游攻略可分为两类, 一类是游览前撰写的预期游览行程, 另一类是游览后撰写的实际游览行程, 本文研究真实游览行程, 因而选择第二类作为研究对象。在进行有效分析之前, 需将每条攻略中所蕴含的景点间流动信息转化为易于分析的数学语言：矩阵。转化思路如下, 如果在一个旅游攻略中存在从景点i到景点j的直接流动, 那么就记为1, 如若不存在, 就记为0, 从而获得一个关系矩阵; 如有攻略涉及到研究范围之外的景点, 那就将与其相连的路径设为无效路径, 而非忽略整个旅游攻略, 转化示意如图1所示。抓取去哪儿网旅游攻略模块中相关网页信息, 将其转化为一系列关系矩阵, 并对所有矩阵进行叠加运算, 从而实现文本信息向数学语言的转换。本研究共收集2012年去哪儿网上有关南京市的实际游览行程攻略1406条, 并最终将其转化为1个45× 45的多值有向关系矩阵。将流动中涉及的景点称为节点, 将两节点间的直接流动称为路径 (E), 将每一个路径上的流动次数称为流量 (l), 将多条路径组成的图形称为流动网络。该矩阵共涉及到节点45个, 路径590条, 流量总和为5195, 笔者通过这个矩阵来分析南京市区景点间流动。需要说明的是, 本文的旅游景点较为宽泛, 既包括传统意义上的旅游景点, 也包括购物街区、酒吧街区、大学校园等旅游场所。

图1

Fig. 1

	Figure Option ViewDownloadNew Window
	图1 旅游攻略的矩阵转换Fig. 1 Matrix from tourism strategy

本文从网络中景点评价相关指标、整体网络评价相关指标和景点作用加权平均距离三个方面来综合评价景点间流动情况, 具体指标如表1所示。计算公式中符号具体含义如下：C_ini、C_outi分别为景点i的流入度和流出度; l_ji为从景点j流向景点i的流量; l_ij为从景点i流向景点j的流量; C_i为景点i的中心度; S_i为景点i的扩散指数; D为网络密度; E为网络的路径数目; C_D为网络中心势; l̅为平均流量; r为流量占比; D_outi、D_ini分别为景点i的流出和流入加权平均距离; d_ij为两景点间的距离; m、n为不同网络中的景点个数。

表1

Tab. 1

表1(Tab. 1)

表1 评价指标 Tab. 1 Evaluation indexes 指标 具体指标 计算公式 结果含义 网络中景点评价相关指标 流入度 Cini=∑j=1nlji (1) 结果数值越大, 景点的流入度、流出度和中心度越强, 在网络中的地位越高。 流出度 Couti=∑j=1nlij (2) 中心度 Ci=Couti+Cini (3) 扩散指数 Si=(Couti-Cini)/Ci×100% (4) 评价景点扩散集聚的强弱, 结果数值越大, 扩散功能越强。 整体网络评价相关指标 网络密度 D=E/n(n-1) (5) 数值介于0~1之间, 结果数值越大, 网络密度越高。 中心势 CD=2∑i=1nmax(Ci)-Ci/(n2-3n+2) (6) 数值介于0~1之间, 结果数值越大, 中心势越强, 分布越不均衡。 平均流量 l̅=∑i=1n∑j=1nlij/E (7) 结果数值越大, 该网络平均流动强度越大。 流量占比 r=∑i=1n∑j=1nlij/∑i=1m∑j=1mlij×100%n⊆m (8) 度量各子网络的重要性, 结果数值越大, 子网络越重要。 景点作用加权平均距离 流出加权平均距离 Douti=∑j=1nlijdij/∑j=1nlij (9) 加权平均距离反映了该景点流出和流入的平均作用距离, 结果数值越大, 作用距离越远。 流入加权平均距离 Dini=∑j=1nljidij/∑j=1nlji (10)

表1 评价指标 Tab. 1 Evaluation indexes

根据公式 (1)-(3), 计算45个景点的3项指标 (图2), 其结果呈现出如下的特征：

(1) 景点中心性和所在景区等级的相关性。从各景点中心度排序结果可以看出, 景点中心性与该景点所在景区等级具有一定的正相关性, 景点中心度越高, 其所在景区的等级也就越高。夫子庙和中山陵中心度排在前两位, 分别达到了1500和1205, 这两个景点是南京仅有的两个5A级景区的核心景点, 也是南京知名度最高的景点。紧随其后的是玄武湖和总统府, 中心度分别为1002和997, 这两个景点同样具有较高的知名度, 为4A级景区的核心组成部分。明孝陵、雨花台的中心性也较高, 均在600以上, 明孝陵为世界文化遗产, 同时也是5A级景区的重要组成部分, 雨花台为4A级景区。古林公园、静海寺等景点的中心性较低, 这些景点等级低, 知名度差。但也有少数景点, 中心性与所在景区等级不匹配, 如鼓楼本身等级不高, 但中心性较高, 而阅江楼为4A级景区核心景点, 但中心性较低。这说明, 景点空间位置也影响着中心性, 鼓楼位于城市中心, 而阅江楼相对偏远。

图2

Fig. 2

	Figure Option ViewDownloadNew Window
	图2 节点的中心度Fig. 2 Centrality of each node

(2) 流动网络中各景点所扮演角色的层级性。为进一步分析各景点在流动网络中所处地位, 笔者对中心度进行层级划分, 通过观察图1中各景点中心度排序曲线斜率变化, 将45个景点划分为5个层级 (表2)。将中心度大于900的景点划分为第一等级, 包含了4个景点：夫子庙、中山陵、玄武湖和总统府, 这些景点在流动网络中处于核心地位, 是市级中心景点; 明孝陵、雨花台、鼓楼3个景点为第二层级, 中心度介于600~900之间, 位于市级中心景点的周边地区, 为市级副中心景点; 中华门、南京大学、鸡鸣寺、湖南路4个景点为第三层级, 中心度数值在300~600之间, 在区域内具有一定影响力, 为区域级中心景点; 大屠杀纪念馆、新街口、瞻园、台城等8个景点中心度介于100~300之间, 为区域级副中心景点; 朝天宫、梅园新村、美龄宫、阅江楼等26个景点的中心度数值小于100, 是一般节点性的景点, 在流动网络中的连接作用较弱, 所起的作用较低。

表2

Tab. 2

表2(Tab. 2)

表2 景点层级划分 Tab. 2 Level distribution of scenic spots 中心度 层级 目录 > 900 市级中心景点 夫子庙、中山陵、玄武湖、总统府 600~900 市级副中心景点 明孝陵、雨花台、鼓楼 300~600 区域级中心景点 中华门、南京大学、鸡鸣寺、湖南路 100~300 区域级副中心景点 大屠杀纪念馆、新街口、瞻园、台城、灵谷寺、长江大桥、莫愁湖、紫金山天文台 < 100 一般性景点 朝天宫、梅园新村、美龄宫、阅江楼、南京博物院、1912、白鹭洲、九华山、明故宫、中山植物园、情侣园、石头城、清凉山、梅花山、燕子矶、海底世界、先锋书店、南京师范大学、东南大学、甘熙故居、云锦博物馆、奥体中心、半山园、静海寺、渡江胜利纪念碑、古林公园

表2 景点层级划分 Tab. 2 Level distribution of scenic spots

(3) 节点在流动网络中的扩散与集聚。依据公式 (4), 计算每个景点扩散指数S_i, 因为景点中心度过小会使S_i失去意义, 为此笔者选择中心度≥ 100的景点进行S_i计算。依据计算结果, 将景点划分为三类：扩散型、平衡型和集聚型 (表3)。中山陵S_i值最大, 为35.44%, 是唯一的扩散型景点; 夫子庙S_i值最小, 为-30.40%, 其次是新街口, 为-28.57%, 这两个景点为集聚型景点; 除这3个景点外的15个景点都为平衡型景点。扩散型景点有更多的游客从景点之外的地方流入, 如酒店、对外交通节点等, 而集聚型景点则有更多的游客从该景点流向景点之外的地方。在南京游览过程中, 中山陵更多的作为一天行程的开始, 而夫子庙、新街口则多作为一天行程的结束, 而后流向酒店或对外交通节点。

表3

Tab. 2

表3(Tab. 2)

表3 景点的扩散与集聚功能类型 Tab. 2 Diffusion and agglomeration function of main scenic spots 类型 扩散型 平衡型 集聚型 Si > 20% [-20%, 20%] < -20% 景点 中山陵 玄武湖、鸡鸣寺、总统府、南京大学、莫愁湖、雨花台、中华门、大屠杀纪念馆、鼓楼、长江大桥、明孝陵、灵谷寺、瞻园、紫金山天文台、湖南路 新街口、夫子庙

表3 景点的扩散与集聚功能类型 Tab. 2 Diffusion and agglomeration function of main scenic spots

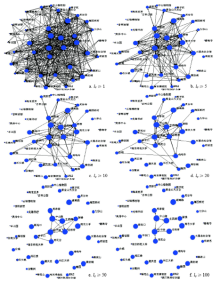
3.2.1 不同流量控制下的流动网络 景点间的流量是存在差异的, 不同流量控制下的网络所涉及的路径和节点是不尽相同的。为此, 需要分析不同流量控制下的网络特征。根据流量差异, 将景点间的路径分为6个层次：l_ij ≥ 1, l_ij ≥ 5, l_ij ≥ 10, l_ij ≥ 20, l_ij ≥ 50, l_ij ≥ 100, 并利用Netdraw软件绘制网络图形 (图3)。统计不同流量控制下流动网络的节点数、路径数和路径流量, 并依据公式 (5)-(8), 计算了各网络的网络密度、中心势、平均流量和流量占比 (表4)。

图3

Fig. 3

	Figure Option ViewDownloadNew Window
	图3 不同流量控制下景点之间流动网络Fig. 3 Networks in different volume of flow

表4

Tab. 4

表4(Tab. 4)

表4 不同流量控制下的流动网络特征 Tab. 4 The characteristic of networks in different volume of flow 流量阀值 节点数 路径数 网络密度 中心势 平均流量 流量占比 lij ≥ 1 45 590 0.298 0.365 8.81 100% lij ≥ 5 30 194 0.223 0.462 23.24 86.80% lij ≥ 10 26 115 0.177 0.459 34.64 76.69% lij ≥ 20 18 62 0.203 0.368 52.48 62.64% lij ≥ 50 8 18 0.321 0.429 99.94 34.63% lij ≥ 100 6 7 0.233 0.400 148.57 20.02%

表4 不同流量控制下的流动网络特征 Tab. 4 The characteristic of networks in different volume of flow

从图表中可以看出, l_ij ≥ 1时, 节点数为45, 包含所有景点, 路径数为590个, 平均流量为8.81, 网络密度为0.298, 中心势为0.365, 中心景点优势不明显, 网络分布相对均衡。l_ij ≥ 5时, 节点数迅速下降为30, 路径数则下降的更为明显, 为194, 下降了67.12%, 说明绝大多数路径流量较小, 联系较弱; 平均流量大幅上升为23.24, 流量占比达86.80%, l_ij ≥ 5的路径主导着网络流动; 网络密度出现下降, 而中心势有所提高, 集中现象较l_ij ≥ 1时明显。l_ij ≥ 10时, 路径下降速度依然快于节点下降速度, 网络密度进一步降为0.177, 平均流量进一步上升, 流量占比依然超过3/4, 中心势相对较高, 达0.459。l_ij ≥ 20时, 节点数和路径数下降为18和62, 网络密度出现上升, 为0.203; 平均流量达52.48, 流量占比超6成, 说明l_ij ≥ 20路径依然可以刻画较多的流动; 中心势较低, 分布均衡。l_ij ≥ 50时, 节点数下降为8, 包含4个市级中心景点、3个市级副中心景点和1个区域级中心景点, 路径数减少到18, 流量占比约为1/3, 平均流量上升为99.94, 网络密度为所有网络中最高, 达到0.321。l_ij ≥ 100时, 节点数进一步下降为6, 这些节点为最核心的景点, 路径数也仅有7, 网络密度为0.233, 但流量占比却达到了20.02%, 平均流量为148.57, 这些路径在景点联系中占有支配地位。从以上的变化中, 可以看出参与的节点数、路径数、流量占比随着流量控制值的增加而减少, 而平均流量随着控制值的增加而增加, 网络密度与中心势与控制值间无明显关系。在控制值的有序变换中, 核心景点和主要路径不断呈现, 核心边缘特征逐渐清晰。

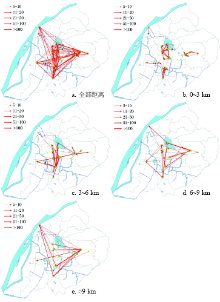
3.2.2 不同距离控制下的流动网络 距离是影响流动的重要因素, 笔者进一步阐述不同流动距离的网络特征。本文通过道路网矢量图的网络分析, 计算两景点间实际通行距离。景点间流量越小, 其产生的偶然性也越大, 为了更好的分析距离的影响, 需要对其进行一定的阀值控制。l_ij ≥ 5路径的流量占比达到了86.80%, 保留了绝大部分的流量。因而本文选取l_ij ≥ 5的路径为研究对象, 这样既保持了大量流动的原真性, 又排除了偶然性的流动。根据距离不同, 景点间路径分为4类：0~3 km, 3~6 km, 6~9 km, > 9 km。依然计算了各相关特征指标 (表5), 并绘制了专题地图 (图4)。

图4

Fig. 4

	Figure Option ViewDownloadNew Window
	图4 不同距离控制下流动网络的空间特征Fig. 4 The spatial characteristic of networks in different distance

表5

Tab. 5

表5(Tab. 5)

表5 不同距离控制下的网络特征 Tab. 5 Characteristics of network in different distance 距离 (km) 节点数 路径数 网络密度 中心势 平均流量 流量占比 全部距离 30 194 0.223 0.462 23.24 100% (0, 3] 29 87 0.107 0.173 27.18 52.45% (3, 6] 23 46 0.100 0.324 22.41 22.87% (6, 9] 17 36 0.132 0.169 18.94 15.12% > 9 14 25 0.137 0.468 17.24 9.56%

表5 不同距离控制下的网络特征 Tab. 5 Characteristics of network in different distance

从图表中可以看出, 全部路径在空间上呈现出四角形格局, 高流量路径呈现出以新街口为中心的十字交叉。在0~3 km区间内, 节点数为29, 路径数为87, 是所有区间节点数和路径数最多的; 平均流量达27.18, 流量占比为52.45%, 同样是各区间最高的, 在整个流动中占有重要地位; 网络密度仅有0.107, 中心势也只有0.173, 中心特征不明显; 在空间上, 景点及其路径主要被分割为3个集聚区, 有近一半的流动在集聚区内完成。在3~6 km区间内, 节点数下降为23, 路径数下降为46, 平均流量下降为22.41, 流量占比大幅下降, 仅有22.87%; 网络密度为所有区间最低, 而中心势较0~3 km区间有明显上升; 在空间上, 无明显分割特征, 0~3 km区间的3个集聚区联系到一起, 呈现出以核心景点为中心的放射性特征。在6~9 km区间内, 节点数进一步下降为17, 路径数下降到36, 网络密度上升为0.132, 平均流量下降为18.94, 流量占比下降为15.12%, 该区间景点间流动更为稀少, 距离效应显著增强; 中心势为各区间最低, 仅为0.169, 分布更为均衡; 在空间上, 整体上呈现出以玄武湖、雨花台、大屠杀纪念馆、中山陵为端点的四边形结构, 其内部以核心景点为中心的放射性特征依然明显。在大于9 km区间内, 节点数仅为14, 路径数也只有25, 网络密度上升为0.137, 平均流量最低, 只有17.24, 流量占比也仅有9.56%, 该区间内景点间流动最少; 中心势是所有区间最高的, 为0.468, 具有一定的中心分布特征; 在空间上, 呈现以雨花台、长江大桥、中山陵为端点的三角形结构, 其内部呈现以中山陵为单中心的放射性特征。从距离变化呈现出的不同特征来看, 随着距离增加, 网络中的节点数、路径数、平均流量、流量占比都逐渐下降, 而其他指标与距离变化并无明显关系。由此可以看出, 距离对景点间流动有着重要影响, 距离衰减规律明显, 景点间距离越远, 流动频率也就越少。

3.2.3 市级中心景点在流动网络中的地位 核心景点在流动网络中占有重要地位, 提取与市级旅游景点相关且l_ij ≥ 5的路径, 从流出、流入两个视角分析市级中心景点在流动网络中的地位 (图5)。统计计算连接节点、流量占比、平均流量等网络指标; 并利用公式 (9) 和 (10), 计算景点的加权平均距离 (表6)。

图5

Fig. 5

	Figure Option ViewDownloadNew Window
	图5 中心景点与其他景点的空间联系Fig. 5 The spatial connection between central scenic spots and others

表6

Tab. 6

表6(Tab. 6)

表6 中心景点参与的网络特征 Tab. 6 The characteristic of networks between central scenic spots and others 景点类型 夫子庙 中山陵 总统府 玄武湖 流出 流入 流出 流入 流出 流入 流出 流入 连接节点 16 22 16 14 18 15 16 13 流量占比 (%) 11.29 23.86 17.65 7.96 11.60 9.67 12.42 8.87 平均流量 31.81 43.59 49.75 25.64 29.06 29.07 35 30.77 加权距离 （km） 3.75 4.58 5.95 6.80 3.58 3.94 3.57 4.82

表6 中心景点参与的网络特征 Tab. 6 The characteristic of networks between central scenic spots and others

表7

Tab. 7

表7(Tab. 7)

表7 回归结果比较 Tab. 7 The comparison of regression analysis 类型 回归方程 R2 幂函数 Tij=7.12×10-4×CoutiCinj/dij0.635 0.652 指数函数 Tij=7.09×10-4×CoutiCinj/e-0.143dij 0.378

表7 回归结果比较 Tab. 7 The comparison of regression analysis

从图表中可以看出, 中心景点涉及面较广, 对整体流动具有较强的支配作用。有38条路径和夫子庙连接, 其中流入22条, 流出16条, 两者流量占全部流动的35.15%, 超过1/3, 夫子庙在整个流动中占有优势。4个景点中, 即便是流量占比最小的总统府也达到了21.27%, 超过1/5。将4个景点叠加, 共计118条路径, 占比60.82%, 流量为3575, 占比79.22%, 这也进一步反映出4个景点在流动网络中的主导地位。从平均流量上来看, 流出流量最大的是中山陵, 为49.75, 流入流量最大的是夫子庙, 为43.59。从流入和流出的平均流量差距上看, 中山陵和夫子庙差距较大, 而玄武湖和总统府差距较小。从加权距离来看, 无论是流入还是流出, 中山陵加权平均距离都是最高的, 这说明中山陵作用距离较远。加权平均距离不仅受景点等级影响, 更多的和其分布区位相关。中山陵位于城区东部, 与其他景点相距较远, 因而其作用距离较远。其他3个景点位于城市内部, 与其他景点相距较近, 因而平均作用距离较近。另外, 各景点流出加权平均距离都小于流入距离, 说明各景点流入影响范围要大于流出影响范围。

通过上述分析可以看出不同景点之间的流动路径是存在差异的。这样的差异体现在两个层面, 一是距离差异, 距离越近, 流动频率越高, 说明距离具有摩擦效应; 二是等级差异, 高中心度景点之间流量较大, 说明景点等级对流量存在影响。基于上述两种现象的分析, 笔者试图构建流动模型, 分析游客在景点之间的流动机制。

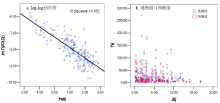
空间流动是空间相互作用的外在表征, 是地理学研究的重要议题, 已有许多成熟的度量方法。在相互作用的研究中, 其中最为重要的是引力模型, 即：I_ij = kP_iP_j/f(d_ij), 其中I_ij为i地和j地之间的作用强度, P_i与P_j分别为i地和j地的吸引力, d_ij为i地和j地之间的距离, f(d_ij) 为距离d_ij的单调递增函数。在实际的计算中, P_i与P_j经常用两地规模来替代, f(d_ij) 通常用d^β (幂函数) 和e^{-β d} (指数函数) 来表示, 并以d^β 居多, β 被称为空间阻尼系数或距离摩擦系数, β 值越大, 对距离越敏感, 作用值衰减速度也就越快。威尔逊进一步发展了引力模型, 基于熵最大化原理, 导出流动模型, 即：I_ij = kO_iD_j/f(d_ij), d_ij与f(d_ij) 的含义不变, I_ij为从i地流入j地的强度, O_i为i地的流出规模, D_j为j地的流入规模。根据O_i和D_j已知与否, 可以将其分为无约束、产出约束、吸收约束和完全约束四种类型。本文研究数据可以准确给出各景点流入量与流出量, 属于完全约束的威尔逊模型。本研究依然选择l_ij > 5的路径作为回归样本, 基于矢量路网计算的实际距离d_ij, 并用T_ij替代I_ij来表示两景点间流量, 用流出度C_outi来替代O_i, 用流入度C_inj来替代D_j。分别选择幂函数和指数函数作为距离函数进行回归分析。运用T_ij、C_outi、C_inj、d_ij样本数据进行回归计算, 在实际计算过程中, 首先要对两个函数进行对数变换, 然后进行线性回归, 其最终回归结果如表7所示。

从回归结果来看, 幂函数回归结果要优于指数函数, 因而本文选择幂函数的威尔逊模型来解释流动机制, 并绘制了该模型的对数回归图 (图6a)。城市内部景点间流动的空间阻尼系数为0.635。在以往人口流动研究中, 学者分别利用移动电话数据和出租车数据来研究城市内部人口迁移, β 值集中于1到2之间^[19-20], 本研究β 值低于这一数值区间。此外, 在利用中国航空旅客数据的城市间长距离流动研究中, 其空间阻尼系数也高于本研究的空间阻尼系数^[21]。这说明距离对游客在城市内部流动的影响既小于长距离出行影响, 也弱于对本地居民日常出行的影响。游客从客源地到目的地过程中需要克服较长的空间距离, 花费较多时间成本和经济成本, 而在目的地城市内部流动所需要克服的距离尺度相对要小的多, 所以其流动摩擦小于长距离流动的距离摩擦。在大交通成本已经投入的前提下, 游客在城市内部对流动具有更强的倾向性, 因而其流动距离摩擦要小于本地居民日常活动的距离影响。利用回归的方程, 计算出所有样本的预测值, 并将观测值和预测值进行比较分析 (图6b), 可以看出两者整体耦合性较好, 但在短距离流量的预测上存在一定的偏差。从以上分析不难看出, 景点间流动是景点流入度、流出度和景点间距离共同作用的结果; 和城市居民流动相比, 游客在城市内部景点间这一特殊流动对距离的敏感度相对较低。

图6

Fig. 6

	Figure Option ViewDownloadNew Window
	图6 流动机制的回归结果Fig. 6 Regression results of flow mechanism

在对不同距离控制下流动网络特征分析的过程中, 可以清晰地看出在0~3 km距离段相关景点聚集为3个组团, 且每个组团内都存在市级中心景点; 结合l_ij > 20流量控制下的景点间流动情况, 提炼出南京目的地景点系统及其景点间流动模式。根据集聚组团将南京市景点划分为3个景点系统：中山陵景点系统、夫子庙景点系统和中心城区景点系统 (图7a)。中山陵景点系统以中山陵为核心, 夫子庙景点系统以夫子庙为核心, 中心城区景点系统以玄武湖、总统府为核心。在实际流动中, 不同系统间主要通过核心景点间的主要流动进行联系, 而系统内部不同景点间主要通过次要流动和一般流动进行连接。从机制模型的推导来看, 景点之间的距离摩擦相对较小, 而景点等级具有更重要的影响, 核心景点之间也更易产生流动, 因而系统间多以其核心景点间流动来构建联系。在此基础上, 绘制了南京旅游目的地系统的空间示意图 (图7b), 3个系统呈相对独立的分布状态。进一步分析各系统核心景点特征, 中山陵景点系统的核心景点中山陵为扩散性型景点, 其系统内部大多呈现出以中山陵为中心的扩散性流动; 夫子庙景点系统的核心景点夫子庙为集聚型景点, 其系统内部流动多为以夫子庙为中心的集聚性流动; 中心城区景点系统的玄武湖、总统府两个核心景点为平衡型景点, 其内部流动多为以这两个景点为核心的平衡型流动。

在景点间流动以及目的地系统划分的基础上, 抽象出更为一般的南京目的地系统结构及其流动模式 (图7c)。依据南京三个景点系统核心景点的不同特征, 可以将目的地系统结构分为三类：多中心平衡结构、单中心集聚结构和单中心扩散结构。在流动模式上, 主要流动形式多存在于主要节点之间, 主导整个系统的流动, 沟通连接着不同的目的地系统; 次要流动多存在于主要景点和次要景点之间, 以及次要景点之间, 主导着系统内部的流动, 且大部分存在于系统内部, 少部分存在于不同系统之间; 一般流动多存在于次要节点和一般节点之间, 以及一般节点之间, 这种形式流动处于整个流动网络的底层, 多存在于系统内部。此外, 需要说明的是, 从南京这一案例地总结出的三种目的地系统结构出发, 还可以进一步推导出其他三种类型的目的地结构, 即：多中心集聚结构、多中心扩散结构和单中心平衡结构, 这三种结构可能存在于其他城市内部。

图7

Fig. 7

	Figure Option ViewDownloadNew Window
	图7 南京目的地系统及其流动模式Fig. 7 Destination systems and flow patterns in Nanjing