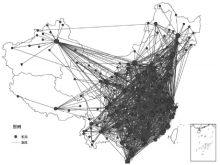
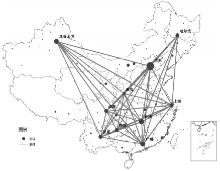
本文收集了截止2012年12月31日中国国内航班数据如图1所示 (台湾目前被分类为国际航线, 本文暂不加以考虑)。由于研究尺度是全国范围, 因此本文将城市抽象为网络节点, 同一城市的机场用该机场所在的城市代表, 而有航班往来的城市用无向边连接。中国航空网络共有城市节点167个, 航线连边1386条, 平均度大小为16.599 (度最大的三个城市分别为北京、上海和广州), 平均路径长度为1.958, 聚类系数达到0.721。

图1

Fig. 1

	Figure Option ViewDownloadNew Window
	图1 中国航空网络 (不含台湾)Fig. 1 Chinese aviation network (excluding Taiwan)

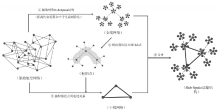
轴辐结构是大部分节点都与少数某些节点连接, 如图2a所示, 可分为单hub结构和多hub结构, 其中多hub结构有种特殊形态, 每个hub形成其局部支配中心, 而所有hub连接起来又构成一棵具有层次性的树, 即引言中提及的Barthelemy在2006年设计的树形轴辐结构 (Tree Hub-Spoke), 如图2b所示, 虚线边连接着各个hub节点, 构成一棵树, 阴影区域的hub节点相比外围hub节点度数更大, 层次更高。在考虑每个节点的地理位置之后, 这种树形轴辐结构的局部hub结构即表现为地域性的聚集性, 而将度数比较大的hub节点彼此连接成互通的枢纽航线^[6], 即能形成图2c所示的航空网络轴辐结构。因此, 从现有网络中抽取图2b所示的树形轴辐结构是构建图2c所示的航空网络轴辐结构的重要环节。又因为该树形轴辐结构同时也是一颗最多叶子生成树, 因而如何根据航空网络的结构特性修改最多叶子生成树算法构建该属性轴辐结构又成为该重要环节的关键部分。

图2

Fig. 2

	Figure Option ViewDownloadNew Window
	图2 网络轴辐结构Fig. 2 Hub-spoke structure of network

本文航空网络轴辐结构的抽取思路如图3所示, 先用距离约束的最多叶子生成树算法从现有的航空网络中抽取树形轴辐结构形成支线网络, 然后从支线网络中抽取hub节点连接成的树形结构, 并选取其中度数比较大的hub节点构成航空枢纽点 (图3中阴影区域节点)。接下来从原始航空网络中抽取这些航空枢纽点之间的连线关系构成干线网络, 最后综合干线和支线网络便形成了航空网络的轴辐结构。

图3

Fig. 3

	Figure Option ViewDownloadNew Window
	图3 航线网络轴辐结构构建思路Fig. 3 The flowchart of generating aviation network hub-spoke structure

生成最多叶子森林是算法的第一步, Lu通过一系列的定理证明, 设计出可以在线性时间内生成一系列的叶子节点最多的子图来构成森林F, 这些子图只由3类点构成：度为1的叶子节点, 度大于等于3的非叶子节点, 以及度为2的节点 (这些节点连接2个度大于3的非叶子节点)。Lu在设计该步骤的原始算法中, 只考虑了图形的拓扑结构, 本文在森林子图的构造过程中进行了距离约束, 在构建森林过程中只考虑了距离小于ds的连边, 其伪代码如图4所示, 下划线加粗部分为算法改进部分。

图4

Fig. 4

	Figure Option ViewDownloadNew Window
	图4 距离约束的最多叶子森林求解伪代码Fig. 4 Pseudo code for creating distance-constraint maximally leafy forest

连接最多叶子森林构成一棵生成树是算法的第二步, Lu的原始连接思想是：筛选出原始图G中未在森林F中出现的边集合UE, 判断UE中边的端点在森林F中是否为叶子节点, 将UE中的边分为“ 非叶子节点连接非叶子节点的边集合II” , “ 非叶子节点连接叶子节点的边集合IL” 和“ 叶子节点连接叶子节点的边集合LL” 三类。然后依次按照II, IL和LL的优先顺序向森林F中添加连边, 直至F构成一棵生成树ST。为了使F中单个点构成的子图能与最近的非叶子节点相连, 维持地域性聚集特征, 本文在给F添加连边前, 分别对II, IL和LL中的边按照其长度len进行了排序, 形成近距离节点优先连接的原则, 伪代码如图5所示, 其中下划线加粗部分为算法改进部分。

图5

Fig. 5

	Figure Option ViewDownloadNew Window
	图5 近距离优先连接原则的伪代码Fig. 5 Pseudo code of principle of preferential connection with short distance

影响距离约束的最多叶子生成树算法运行结果的关键因素是“ 约束距离” 的确定。如果约束距离选择过大, 约束过宽, 所求出的结果与不考虑距离约束的拓扑求解结果基本类似, 体现不出地域性的聚集; 如果约束距离选择过小, 则会因为参与构建森林子图的连边过少, 生成很多单个点的子图, 影响hub的形成。根据现实的航线设计经验, 远途的航线少而集中, 例如图1中大部分东部的机场都只和西北部的乌鲁木齐相连; 而近距离的城市通航的可能性又比较低, 例如北京与天津、深圳与广州等。因此, 必然有一个最适当通航的距离存在, 如果找出该距离作为算法中的“ 约束距离” , 一方面可以保证约束距离不至于过大, 形成地域性聚集, 另一方面也能保证参与构建森林子图的连边数量, 突显hub节点。为了衡量找出最适当通航距离, 本文计算了中国航空网络“ 距离与连接概率关系图” , 用于定量衡量城市距离与通航航线出现可能性之间的关系, 如图6所示。其计算公式如公式 (1) 所示, 其中P_d表示连接概率, d表示距离, G表示现有航空网络, K_n表示由现有航空网络中的节点所生成的完全图, 而#G(d) 和#K_n(d) 分别表示网络G和K_n中连边长度小于d的连边个数。

Pd=#G(d)#Kn(d)(1)

距离与连接概率关系用于衡量不同距离下, 网络中连边出现的概率大小, 是空间网络中常用的衡量指标之一^[23]。从计算所得的图6中可以明显发现两个城市距离相距过小和过大, 存在航线的可能性都比较小, 而中间距离区间600~700 km连接概率最高, 并在693 km处取得峰值, 连接概率最大为0.163。该概率关系曲线与上文中现实生活航线设计经验相符, 因此, 本文将693 km作为最优“ 约束距离” 参与中国航空网络树形轴辐结构的抽取。

图6

Fig. 6

	Figure Option ViewDownloadNew Window
	图6 中国城市航线网络距离-连接概率关系Fig. 6 The relationship between distance and connection-probability of Chinese aviation network

在最优距离693 km的约束下, 抽取中国航空网络的树形轴辐结构, 形成支线网络如图7所示, 图中节点的大小都表示度的大小。度数排名前10位的节点分别是：北京, 上海, 广州, 长沙, 哈尔滨, 乌鲁木齐, 昆明, 西安, 成都, 贵阳, 这些节点构成中国航空网络的航空枢纽点。该10个点在地理分布上都表现为局部hub节点, 分别支配着各自区域内的其他机场 (如图7阴影区域所示)：乌鲁木齐支配着西北地区; 哈尔滨支配着东北地区; 北京支配着华北地区; 长沙和贵阳支配着华中地区; 西安、成都和昆明支配着大部分西部地区; 广东支配着南部沿海地区; 上海则支配着东部沿海地区。从图7中不难发现, 有些节点在地理分布上并没有表现出就近原则, 反而与距离较远的点相连, 如图中与广州相连的大部分节点, 以及西北部未与乌鲁木齐连接的节点。造成这种现象的主要原因是那些不遵循就近原则的节点与最近的hub节点在原图中就不存在航线, 因此在抽取出来的树形轴辐结构中自然也不会存在。

图7

Fig. 7

	Figure Option ViewDownloadNew Window
	图7 中国城市航线网络的树形轴辐结构Fig. 7 The tree-shaped hub-spoke structure of Chinese aviation network

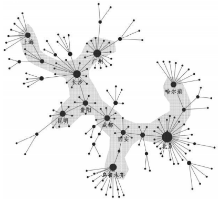
绘制支线网络的拓扑结构如图8所示, 阴影区域为10个枢纽点在拓扑上构成的树形结构, 节点的大小表示度的大小。图中处于外圈的节点是上海、广州、昆明、乌鲁木齐和哈尔滨, 这五个地方在地理上也都处于航线网络的边缘地带; 而另外五个节点不仅拓扑上处于树形结构的内层, 在地理上也处于中国内陆地区。形成这种拓扑结构和地理分布相吻合的现象, 是由构建过程中先进行距离约束构建子图, 再次依次根据近距离优先连边原则连边的构造过程所决定的。然而, 更关心的是这10个节点在原图中的连接关系, 即骨干网的构建。

图8

Fig. 8

	Figure Option ViewDownloadNew Window
	图8 中国城市航线网络的树形轴辐结构拓扑图Fig. 8 The tree hub-spoke topology structure of Chinese aviation network

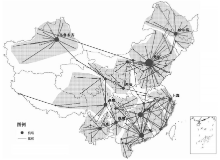
从图1所示的原始航空网络中抽取出10个航空枢纽点之间的连边, 构成图9所示的中国城市航线网络的骨干网。将此干线网络与图7的树形轴辐结构结合即得到了中国城市航线网络的轴辐结构, 其拓扑结构如图10所示。图9显示的干线网络形如中国疆土, 基本覆盖了整个中国, 而图10的航线网络的轴辐结构中枢纽点高度耦合, 每一个枢纽点都支配着相近地域内的其他节点, 非常适合网络流在hub节点集中产生、传播和终结, 降低整个网络流的消耗, 形成一种有序的规模化运输体系。

图9

Fig. 9

	Figure Option ViewDownloadNew Window
	图9 中国城市航线网络的骨干网Fig. 9 The backbone of Chinese aviation network

本文是考虑了机场在国内航线中的连接关系, 筛选了10个支配Spoke点数比较多的Hub节点作为枢纽点, 而金凤君等人根据机场的国内地位、国际地位及枢纽动态性等方面筛选了9个符合实际经济发展情况的城市作为航空枢纽点, 两者的结果对比如表1所示。以下重点讨论航空枢纽点选择的不同之处, 对应枢纽点地理分布, 本文所筛选的长沙和哈尔滨分别对应于金凤君等人筛选的武汉和沈阳, 而且新增了贵阳为航空枢纽点。

表1

Tab. 1

表1(Tab. 1)

表1 轴辐结构构建对比 Tab. 1 Comparative analysis with related research 角度 本文实验 金凤君等人的实验[6] 航空枢纽点 北京, 上海, 广州, 成都, 乌鲁木齐, 昆明, 西安, 长沙, 哈尔滨, 贵阳 北京, 上海, 广州, 成都, 乌鲁木齐, 昆明, 西安, 武汉, 沈阳 干线网络 由航空枢纽点之间的所有连边构成 由航空枢纽点之间的所有连边构成 支线网络 由抽取的树形轴辐构成, 同时考虑了现有航线和距离约束所形成的地域性聚集 只考虑了距离约束的地域性聚集 构建思路 从图论和地理学的角度出发, 直接从现有网络中抽取, 先构建支线网络, 找出枢纽点, 再构建干线网络 从人文地理和经济地理角度出发, 采用人工手动构建方式, 先找出枢纽点, 构建干线网络, 再构建支线网络 优缺点 便于根据现有网络快速进行调整, 效率高, 但为了更好的经济发展需做局部的人工调整 更加适合经济发展, 但人工构建主观性强, 效率较低

表1 轴辐结构构建对比 Tab. 1 Comparative analysis with related research

(1) 长沙和武汉在原图中航班数分别为50和54, 在原图中的航空地位基本相当。结合其他交通运输方式的综合运输能力来看, 武汉是九省通衢, 铁路、公路和河运等交通枢纽都非常的发达, 尤其是近两年开通的高铁, 处于横纵线的交汇点, 极大的替代了航空网络的运输地位; 而长沙相比武汉而言更需要航空网络来支持发展, 因此从此角度来看将枢纽点设在长沙具有一定的发展意义。然而从地理空间分布来看, 长沙离广州过近, 反而武汉的地理位置更加合理。然而本文算法选择长沙的主要原因是：原图中与武汉通航的大部分机场都与其他几个航空枢纽点相连, 因此与武汉连接的大部分节点都已被其他航空枢纽点支配, 而使得长沙在支线网络中的度数更大, 被选中成为航空枢纽点。由于本文只是提出一种轴辐结构构建的通用方法, 建议决策者在实际网络优化中再根据经济发展布局等其他因素做局部调整, 而本文在后续研究中也会进一步根据航空网络的“ 空间结构特性” 对算法做进一步的优化。

(2) 哈尔滨和沈阳在原图中航班数分别为35和37, 在原图中的航空地位也基本相当。从图9中可以发现, 哈尔滨在东北区域控制的范围更加广阔, 而沈阳还有海上航线的运输通道, 而且沈阳支配的区域也处于北京的支配区域范围内, 因此相比而言将枢纽点设在哈尔滨也更加能协助东北内陆地区的经济发展。

(3) 本文新增的贵阳枢纽点处于中国海拔的第二梯度, 而且是内陆地区, 铁路、公路和海运都无法满足其周边的发展, 只能依靠航空, 而且贵阳所支配的节点也较多, 在原网络中航班数也达到35的中上等水平, 贵阳和昆明一起覆盖了第二梯度的云贵高原地区。而中国海拔第一梯度的青藏地区, 本文还未构建出一个强有力的枢纽点, 主要是由于航班数还不足以形成枢纽点, 但随着发展的趋势, 拉萨很有可能发展为西藏区域的枢纽点, 而青海地区要么被兰州支配, 要么独立形成西宁为枢纽点, 这些都要随航空网络的发展进一步调整。

(1) 从干线网络构建方法来看, 金凤君等人将干线网络细分为国内主干线、国内干线和一般干线; 而本文是直接将各枢纽点在原图中现有的所有航线都抽取出来, 并没有进一步细分。如图10所示, 各枢纽点间连接构建的干线网络应该尽量接近完全图, 两两之间都通航, 以加快网络流的集中交换。如果需要进一步划分等级, 本文认为应该利用各枢纽点间的航班数来确定会更加合理, 航班数大的为主干线, 应该重点关注, 航班数小的为一般干线, 应尽力维护使其尽快升级为主干线。

图10

Fig. 10

	Figure Option ViewDownloadNew Window
	图10 中国城市航线网络的轴辐结构拓扑图Fig. 10 The hub-spoke topology structure of Chinese aviation network

(2) 从构建的干线网络结果对比来看, 由于两种方法选取的航空枢纽点基本相同, 而干线网络又是航空枢纽点间的航线, 因此两种方法所构建的干线网络外部形态基本相同, 整体形如中国疆土。另外, 由于本文航空枢纽点中哈尔滨取代了沈阳, 使得本文所构建的干线网络在东北部覆盖更加全面; 而长沙和武汉地理位置基本相当, 并没有对中部的干线网络造成过大的差异。除此之外, 从两种方法构建的干线网络中都能发现, 中国西南部的青藏地区由于缺少一个强有力的枢纽点, 并未被干线网络覆盖, 建议重点加强该地区应的航空建设。

(1) 从支线网络的划分距离来看, 金凤君等人参考了其他学者的一些研究成果, 直接将构建支线网络的距离阈值设置为800 km; 而本文从网络航线距离与其连接概率的关系出发, 选取了连接概率最大所对应的距离693 km作为划分距离, 更加客观, 符合现有网络的特点。连接概率最大, 表示在当前网络中这种连边关系出现的概率最大, 那么在这个距离点上各城市间形成航线的可能性也就更大, 加之本文算法的最多叶子保证, 将其设为截断阈值所能划分出的地域支配集合和Hub节点会更加明显。

(2) 从构建的支线网络结果对比来看, 同样由于两种方法选择的航空枢纽点基本相同, 而支线网络是围绕航空枢纽点的局部聚集性支配性航线网络, 因此两种方法所构建的支线网络大部分结构相同。然而, 金凤君等人所构建的支线网络在黑龙江、甘肃、西藏、内蒙古和新疆等多个地区都存在较多城市串航的网络, 而本文所构建的支线网络一方面由于选择黑龙江作为航空枢纽点, 另一方面也受最多叶子生成树的连通特性作用 (如甘肃地区的偏远点, 同时与乌鲁木齐和西安两个航空枢纽点相连), 使得城市串航这种低效运输情况大大减少, 只在西藏和甘肃等地出现。