中国区域创新的时空动态分析

引用本文

程叶青, 王哲野, 马靖. 中国区域创新的时空动态分析. 69(12): 1779-1789
CHENG Yeqing, WANG Zheye, MA Jing. Analyzing the space-time dynamics of innovation in China. Acte Geographica Sinica, 69(12): 1779-1789 复制到剪切板

Permissions

本文是开放获取期刊文献，在以下情况下可以自由使用：学术研究、学术交流、科研教学等，但不允许用于商业目的.

中国区域创新的时空动态分析

程叶青^1,², 王哲野³, 马靖⁴

1. 海南师范大学地理与旅游学院, 海口 571158

2. 中国科学院东北地理与农业生态研究所, 长春 130102

3. Department of Geography, Kent State University, Kent 44242, Ohio, USA

4. 深圳中学, 深圳 518001

作者简介：程叶青 (1976-), 男, 湖南武冈人, 博士, 副研究员, 中国地理学会会员 (S110006162M), 主要从事经济地理与乡村发展研究。E-mail: yqcheng@iga.ac.cn

基金:中国科学院重点部署项目 (KZZD-EW-06, KSZD-EW-Z-021); 教育部人文社会科学重点研究基地重大项目 (13JJD790008)

摘要

基于探索性空间数据分析和验证性空间面板模型,本文探讨了2000年以来中国区域创新的时空动态。结果表明：① 自创新战略实施以来,中国各省区创新产出的年均增长率几乎都经历了一个剧烈的加速过程,说明区域创新能力的总体提升,但是,东部沿海地区仍然在创新产出中居于压倒性地位,导致“沿海—内陆”分化加剧和区域鸿沟的进一步突出,省区创新可能会陷入“强者愈强,弱者愈弱”的“马太效应”;② 中国区域创新产出与创新投入的空间集聚随时间推移不断强化,通过识别不同时期各变量“热点”,表明创新产出“热点”地区与创新投入“热点”具有高度的时空耦合特征;③ 人均GDP、研发投入、研发人员及在校大学生数对省区创新产出有显著的直接影响。省区间创新活动存在明显的空间溢出效应,其知识溢出的地理区域跨越了省区边界。空间依赖性的存在导致省区间创新活动具有反馈效应,相邻省区的知识溢出对该省区的创新活动具有实质性影响。

关键词: 区域创新; ESDA; CSDA; “热点”; 面板空间杜宾模型; 知识溢出; 中国

Analyzing the space-time dynamics of innovation in China

CHENG Yeqing^1,², WANG Zheye³, MA Jing⁴

1. College of Geography and Tourism, Hainan Normal University, Haikou 571158, China

2. Northeast Institute of Geography and Agroecology, CAS, Changchun 130102, China

3. Department of Geography, Kent State University, Kent, Ohio 44242, USA

4. Shenzhen Middle School, Shenzhen, Guangdong 518001, China

Fund:Key Research Program of the Chinese Academy of Sciences, No.KZZD-EW-06-03, No.KSZD-EW-Z-021; Key Project of the Ministry of Education of China, No.13JJD790008]

Abstract

Through an integration of exploratory spatial data analysis (ESDA) and confirmatory spatial data analysis (CSDA), this study examines the space-time dynamics of regional innovation at the provincial scale in China from 2000 to 2011. The results show that: firstly, since the implementation of national innovation strategy, the annual growth ratio of innovation outputs of the provinces in China has experienced a drastic process of acceleration, which suggests the overall improvement of regional innovation capabilities. However, an overwhelming status in growth rate still belongs to eastern region, leading to the rise of the coastal-interior division and the divergence among regions, and regional innovation in China may fall into the “Matthew Effect” that the strong will become stronger and the weak will be constantly weaker. Secondly, regional innovation outputs and inputs in China experience an increasing change of spatial clustering over time. Various types of hot spots are identified over time, revealing that innovation hot spots overlay well with other variables. Finally, the selected explanatory variables, such as GDP, RDE, RDP and PCH, have significant direct impacts on provincial innovation in China. There exist obvious spatial spillover effects in provincial innovation activities, and the geographic region of which has crossed the provincial border. The spatial dependence of innovation activities gives rise to the feedback among the provinces, and the acknowledge spillover of adjacent province have material influence on a specific province.

Keyword: regional innovation; exploratory spatial data analysis; confirmatory spatial data analysis; hot spot; spatial panel Dubin mode; acknowledge spillover; China

Show Figures

1 引言

在经济全球化背景下, 世界各国都关注到创新对经济发展的至关重要作用^[1]。新经济增长理论认为知识型创新是促进经济增长和提高生活标准的主要驱动力^[2], 研发过程中通过资源投入产生新的知识, 其扩散过程是现代市场经济增长机制的核心^[3]。创新是一种以新的方式生产新知识或融合已有知识的过程, 知识为创新性价值创造 (譬如创新过程) 奠定了最为重要的基础^[4]。然而, 知识创新来源于一定的支撑 (如企业、研究机构和高等教育机构等), 而这些支撑又趋向于集中在某些具体区位, 这就决定了发明和创造不会均衡分布于空间, 而是趋向于在一定区位聚集^{[5, 6]}。实证研究证明, 知识流动遵循地理衰减规律, 意味着地理距离的增加会提高知识传播成本^{[7, 8]}。区域创新系统中的创新人员依赖空间邻近性从其它人员获益, 由于创新过程复杂性的提升, 创新人员趋向于从各种来源吸收和整合新的或互补知识, 由此, 其他处于相邻区位的人员无疑成为获取知识最经济的选择。此外, 某一区域创新人员生产的新知识将随着时间的推移不仅会扩散到同一区域的其它创新人员 (区内知识溢出), 而且会扩散到其他区域的创新人员 (区际知识溢出) ^[9]。事实上, 为了生存和跟上日益白热化全球创新竞争的步伐, 区域创新系统的关键人员不得不寻找更多地理区位较远的知识来源, 导致近几十年来跨区域的知识溢出如雨后春笋般涌现。

针对知识溢出如何测度问题, 国外学者存在争论。Krugman 认为知识流动是看不见的, 知识溢出的实证测度是不可能的^[10]。但是, Jaffe等认为专利记录可能很好的留下知识溢出的纸质痕迹, 因此, 专利引证可以被视为知识溢出的一个指标^[11]。知识溢出的强度可以通过引入空间距离作为解释变量的专利引证强度进行评估, 这种空间相互作用模型已被大量的实证研究所采用^[12]。此外, 引入研发投入的知识生产函数被也被用于识别和测度知识溢出, 在该函数中, 创新产出既取决于“ 区域内部” 研发投入, 也取决于通过地理邻居获取的研发投入^{[13, 14]}。随着空间计量经济学快速发展, 空间计量模型逐渐被应用于分析区域创新和知识溢出效应^[15]。正如Autant-Bernard指出, 创新过程具有明确的空间异质性和空间依赖性, 在知识生产函数中, 通过空间计量工具中的空间自相关可正确计算出模型系数, 且能区分其直接和间接影响^[12]。然而, 除了Lesage等通过解释知识溢出来源地和目的地区域的异质性纠正空间自相关模型外, 现有研究极少将空间计量工具引入到空间相互作用模型的分析框架^[16]。

中国针对知识溢出的文献日益增多, 空间计量工具在知识生产函数中的应用研究快速增长^{[17, 18]}, 空间误差模型和空间杜宾模型等被应用于阐释高校学术研究溢出效应和高新技术产业创新等领域^{[19, 20]}, 研究表明, 知识溢出随地理距离而变化^[21], 研发人员对区域创新有积极的溢出效应^[22]。但是, 已有研究主要从创新投入视角分析了区域知识溢出效应, 未能突出创新产出溢出效应在创新活动中的重要作用^[23]。本文试图从创新投入和创新产出的视角, 应用空间面板杜宾模型定量识别和测度知识创新的溢出效应。

创新活动在地理空间上的分布是不均衡的, 具有高度创新活动的区域往往非常邻近, 表明创新活动存在空间依赖性, 可被视为知识溢出效应在区域间的空间相互作用。因此, 为阐明区域创新的时空动态, 必须考虑空间自相关。GIS技术及探索性数据分析方法 (Exploratory Spatial Data Analysis, 简称ESDA) 为区域发展的空间分析提供了强有力的工具, 且ESDA在近年来区域发展不平衡的实证研究中得到广泛应用^{[24, 25]}, 一些最新的研究也应用该方法探讨了知识创新的空间分布等问题^{[26, 27]}。然而, ESDA实质上是一种数据驱动型方法, 因此在一定程度上缺乏与其它理论模型比较的解释力。为了解决这个问题, 本文在知识生产函数中选择了一些创新投入变量, 以阐明其与创新产出变量间的时空耦合特征。此外, 采用验证性空间数据分析方法 (Confirmatory Spatial Data Analysis, 简称CSDA), 结合知识生产函数和空间杜宾面板模型, 定量研究创新产出与创新投入之间的时空关系, 并着重探讨创新投入和创新产出的溢出效应, 进而阐明中国区域创新的时空动态, 旨在为国家创新发展及战略制定提供有益的参考。

2 研究方法

2.1 知识生产函数模型

本研究以中国31个省 (直辖市、自治区) 为基本空间单元, 分别采集1999-2011年各省级单元数据, 由于缺乏统计数据, 香港和澳门特别行政区和台湾省未被纳入研究范畴。已有文献大多以专利作为创新产出的定量指标^{[28, 29, 30]}, 尽管学术界在探讨哪些指标最适合测度创新产出的问题上未形成共识, 所选择的指标也仅能部分地反映区域创新程度^[31]。但是, 专利在创新过程中的每个阶段都扮演重要角色, 专利数据为分析区域知识创新的时空分布提供了重要的信息^{[32, 33]}, 仍然是到目前为止刻画知识创新最为合适与常用的指标。因为无论专利最终被批准与否, 申请这个产权都包含了支持者重要的成本, 并注重发明相关的新颖性和盈利能力特征^[34]。因此, 本研究仍将专利申请数作为衡量创新产出的表征指标, 并基于最先被Griliches 验证并经过不断发展的知识生产函数^[15], 采用Jaffe的分析框架^[28], 选择4个创新投入变量作为衡量区域创新的决定性因素。Cohen and Klepper指出研发工作是知识创新最重要源泉^[35]。除了研发工作, 内生经济理论强调另一个生产决定性因素的经济理念：技术绩效的经济综合水平^[36]。因此, 将另外两个变量替代知识生产力的整体经济源纳入知识生产函数。这样, 本研究采用的知识生产函数模型为：

$\begin{matrix} PA T_{i, t} = f (RD E_{i, t - 1}, RD P_{i, t - 1}, PC H_{i, t - 1}, GD P_{i, t - 1}) \end{matrix}$ (1)

式中：PAT是指专利申请数; RDE为研发支出; RDP为研发人员数; PCH为在校大学生数; GDP表示国内生产总值。借鉴已有研究成果^{[37, 38]}, 采用滞后一年的创新投入变量, 由于输入变量与可度量的产出变量间的转化需要一些时间, 采用一年时间的滞后可提升观测值的数量和自由度。为了保持输入变量和产出变量数据的一致性, 需对所有变量进行标准化处理。其中, 专利申请数和在校大学生数分别除以总人口数, 以获得人均数; 研发支出除以总人口数, 获得人均研发支出; 研发人员数用与总雇用相关的研发人员代替。原始数据均来源于《中国统计年鉴》(2000-2012) 和《中国科技统计年鉴》(2000-2012)^{[39, 40]}, 为保持数据的可比性, 各省级单元所有GDP数据均转换为1999年不变价。

2.2 ESDA：空间自相关分析

ESDA是一种在评估和测试之前描述性动态因素来解释空间格局的较为复杂的回归模型^[41], 其独特之处在于通过空间权重矩阵建立本区域与周边邻域之间的空间关系, 并通过空间滞后向量确定每一个区域的空间邻域状态^{[41, 42]}。一般采用全局空间自相关 (Moran's I或Geary's C) 和局部空间自相关 (G统计量、Moran散点图和LISA) 来衡量。

Moran's I是测度全局自相关最为常用的指标。本研究采用全局Moran's I统计量测度中国各省级空间单元及其邻阈知识创新的空间关联及差异程度, 该统计量可表达为：

$\begin{matrix} I_{t} = \frac{N}{S_{o}} . \frac{\overset{N}{\sum_{i = 1}} \overset{N}{\sum_{j = 1}} w_{ij} z_{i, t} z_{j, t}}{\overset{n}{\sum_{i = 1}} \overset{n}{\sum_{j = 1}} z_{i, t} z_{j, t}} \end{matrix}$ (2)

式中：W_ij为某一要素的空间权重矩阵; z_it和z_jt表示观测值偏离i和t平均值的程度; N为观测值数量; S_o为所有要素权重的总和。Moran's I 取值范围为[-1, 1], 值趋向于+1, 表明绝对的空间正相关, 高值区域或低值区域趋于集聚; 趋向于0, 表明空间随机分布; 趋向于-1, 表明绝对的负相关, 高值区域被低值区域包围或低值区域被高值区域包围。Moran's I是基于999种排列的排列方法统计推论而得^[43]。

局部空间自相关 (LISA) 认为每个空间单元彼此邻近, 可有助于识别创新投入和创新产出的“ 热点” ^[44]。LISA地图可以刻画局部Moran's I统计量的区位, 也能识别一些有影响的观测值的“ 热点” 。局部Moran's I统计量可表达为：

$\begin{matrix} I_{i} = \frac{z_{i}}{\overset{n}{\sum_{j = 1}} \frac{z_{j}^{2}}{N}} . \overset{N}{\sum_{j = 1}} w_{ij} z_{j} \end{matrix}$ (3)

式中：z_i和z_j为观测值偏离i和j平均值的程度; I_i的期望值 $\begin{matrix} E (I_{i}) = \frac{1}{N - 1} - \overset{N}{\sum_{j = 1}} w_{ij} \end{matrix}$ 。如果I_i大于期望值, 观测值i具有正的空间自相关特征; 如果I_i小于期望值, 则存在负的空间自相关。统计结果服从x(I) = [I - E(I)]/sd(I), 其中sd(I)为I的标准偏离程度。叶信岳和吴林通过叠加不同年份的“ 热点” , 提出了一个时间稳定性“ 热点” 图式, 将Anselin的LISA 意义地图拓展到时序关联^[45]。本研究采用这种方法, 可视化中国多年创新投入和创新产出的空间格局, 并识别其“ 热点” , 旨在以探索性视角阐明中国区域创新投入和创新产出的时空动态关系。

2.3 CSDA：空间回归分析

在当前的研究中, 通过整合知识生产函数, 空间面板回归模型被用于从验证的视角阐明创新投入和创新产出的时空关系, 并解决空间自相关问题和估算空间溢出效应的影响。正如Anselin等指出, 在阐明观测值的空间依赖 (空间自相关) 时, 空间面板数据模型可能包含一个空间滞后因变量或一个空间自回归过程的误差项^[46]。前一个为空间滞后模型 (Spatial Lag Model, 简称SLM), 后一个即为空间误差模型 (Spatial Error Model, 简称SEM)^[47]。空间杜宾模型 (Spatial Durbin Model, 简称SDM) 被认为是第三种空间面板数据模型, 采用这种模型的动机源于当处理区域数据样本时可能会增加遗漏变量等问题, 表明SDM的一个本质特征是因变量中嵌套了空间依赖, 自变量和误差项的参数估计不会受到遗漏变量空间依赖程度的影响^[48]。本研究采用SDM的另一个原因在于测度区内及区际尺度知识溢出效应的可行性, 即知识创新的直接效应和间接效应^[49]。设定省级单元为 i = 1, ..., 31, 时间序列为 t = 1, ..., 12, 时域为2000-2011年, 共12年。量化区域创新投入和创新产出关系的SDM模型如下：

$\begin{matrix} y_{it} = δ \overset{n}{\sum_{j = 1}} w_{ij} y_{jt} + β \overset{n}{\sum_{j = 1}} r w_{ij} x_{i, j, t - 1} + μ_{i} + λ_{t} + ε_{it} \end{matrix}$ (4)

式中：δ 表示空间回归系数; w_ij是空间权重矩阵W中的一个元素; y_jt表示被解释变量在j单元t时期的观测值; x₍_i_,_t_-1) 是i单元和t-1时刻自变量的行向量 (1, K); γ 为k维列向量, 表示空间滞后解释变量的系数; μ _i表示空间固定效应, 其控制了所有空间固定且不随时间变化的变量; λ _i表示时间固定效应, 其控制了所有时间固定且不随空间变化的变量; ε _it表示空间自相关误差项。如果将μ _i看作是一组随机变量而不是一组固定效应, 则SDM就成为随机效应模型。

3 结果与分析

3.1 创新产出的空间分布

中国经济保持了30多年的高速增长态势, 但是, 这种经济增长主要受劳动密集型和出口导向型制造业的推动。中国政府已经认识到创新对国家未来经济发展的重要性, 并且在引导国家创新系统发展中起到了核心和持久的作用^[50]。2006年以来, 随着国家创新战略和《国家中长期科技发展规划 (2006-2020)》的实施, 科学、技术和教育的发展促进了中国区域创新产出的快速增长。统计数据表明, 2000-2011年, 中国的专利申请数从140339项增加到1504670项, 年均增长率达24.07%。其中, 东部沿海发达省份对创新产出的时空格局具有重要的影响, 其专利申请数占全国专利申请总数的65%以上, 专利申请的比重也由65.28%提高到74.74% (表1)。分析表1, 中西部地区19个省区的专利申请数仅占全国的35%, 其在全国的地位持续下降。值得指出的是, 东部沿海地区一些省份的创新产出能力甚至能与整个中部或西部地区抗衡。例如, 广东省2006年专利申请数为90886项, 而同期中部和西部地区申请专利数仅分别为60096项和35857项, 同样, 2011年江苏省专利申请数超过中西部地区的总和, 由此可见, 中国创新产出的空间分布极不平衡。表1显示, 自2006年以来, 中国各省区创新产出的年均增长率几乎都经历了一个剧烈的加速过程, 表明创新能力的总体提升, 但是, 东部沿海地区仍然在创新产出中居于压倒性地位, 导致“ 沿海— 内陆” 分化加剧和区域鸿沟的进一步突出, 中国区域创新可能会陷入“ 强者愈强, 弱者愈弱” 的“ 马太效应” 。

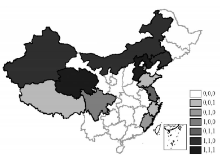
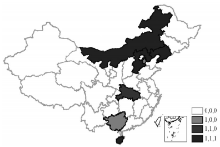
为更清楚地阐明中国区域创新产出的空间分布特征, 本研究基于ArcGIS技术平台, 采用自然断裂点方法, 按照2000年、2006年和2011年的专利申请数分别将中国31个省区划分为5类 (图1)。图1表明, 中国省区创新活动呈现明显的空间分布特征：① 大部分创新活动主要集中在广东、江苏、浙江等几个东部沿海发达省份; ② 高密度创新活动的省份在地理空间上趋于集聚。因此, 可依据区域创新产出的空间特征, 将中国划分为东部沿海创新带和中部内陆创新区两部分。2000年以来, 东部沿海创新带的创新活动密度更高, 并表现出稳定的时空演化特征; 中部内陆创新区主要包括陕西、湖北、重庆、四川、湖南等省区, 并有不断向陕西、重庆、湖北等省区集聚的态势, 导致中国创新产出更为集中的空间分布格局。

表1 2000-2011年中国各省区专利申请数及增长率 Tab. 1 Growth rates of patent applications in China, 2000-2011

3.2 创新产出和创新投入的时空动态

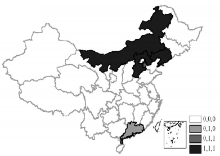
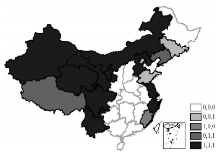
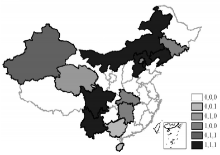
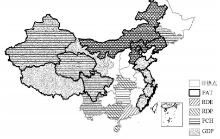
3.2.1 探索性空间数据分析表2揭示了2000-2011年中国创新产出与创新投入的全局空间自相关特征, 除了PCH的全局空间自相关有所波动之外, 其他所有指标均在空间上趋于集聚。但是, 全局空间自相关分析可能掩盖局部空间信息, 会产生一系列问题, 时间关联分析中需要纳入局部空间信息^{[51, 52]}。因此, 本研究通过叠加不同时间截面创新产出和创新投入变量的“ 热点” , 采用时间稳定性“ 热点” 图式方法解决这个问题^[45]。如果某个省区3个时间截面 (2000年、2006年和2011年) 仍为创新产出或创新投入的“ 热点” , 将省区识别为“ 1, 1, 1” ; 如果某一省区除2000年外均为“ 热点” , 标识为“ 0, 1, 1” ; 如果某一省区在3个时间截面中都不是“ 热点” , 则标识为“ 0, 0, 0” 。图2-图7显示了PAT、RDE、RDP、PCH和GDP的时间稳定性“ 热点” 类型。其中, 12个省区的专利申请数可识别为6类“ 热点” ; 5个省区的研发支出可识别为3类“ 热点” ; 16个省区的人均GDP可识别为4类“ 热点” ; 14个省区的在校大学生数可识别为5类“ 热点” ; 7个省区的研发人员可识别为3类“ 热点” 。此外, 专利申请数和人均GDP的“ 热点” 在空间分布上相似, 但具有不同的时间稳定性分布格局 (图2和图4), 而研发支出和研发人员数的“ 热点” 在空间分布和时间稳定性上具有一致性 (图3和图6)。图7显示了5个变量叠加后的时间稳定性“ 热点” 分布格局, 由此看出, 中部省区并未形成显著规模的创新产出“ 热点” 。

表2 创新变量的Moran's I Tab. 2 Moran's I of innovative variables

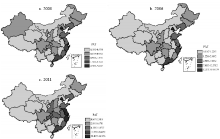	Figure Option View Download New Window
	图1 2000、2006和2011年中国各省区专利申请数Fig. 1 Patent applications in 2000 (a), 2006 (b) and 2011 (c) (piece per 10, 000 persons) in China

	Figure Option View Download New Window
	图2 中国PAT时间热点 (2000, 2006, 2011年)Fig. 2 Temporal hot spots of PAT in China(2000, 2006, 2011)

	Figure Option View Download New Window
	图3 中国RDE 时间热点 (1999, 2005, 2010年)Fig. 3 Temporal hot spots of RDE in China (1999, 2005, 2010)

	Figure Option View Download New Window
	图4 中国GDP时间热点 (1999, 2005, 2010年)Fig. 4 Temporal hot spots of GDP in China (1999, 2005, 2010)

	Figure Option View Download New Window
	图5 中国PCH时间热点(1999, 2005, 2010年)Fig. 5 Temporal hot spots of PCH in China (1999, 2005, 2010)

	Figure Option View Download New Window
	图6 中国RDP时间热点 (2000, 2006, 2011年)Fig. 6 Temporal hot spots of RDP in China (1999, 2005, 2010)

	Figure Option View Download New Window
	图7 中国综合时间热点 (2000, 2006, 2011年)Fig. 7 Comprehensive hot spotsin China in China (2000, 2006, 2011)

3.2.2 验证性空间数据分析采用SDM对创新产出和创新投入进行测试和估算^[53]。首先, 选择具有随机效应的SDM 进行测试, Hausman 测试结果 (11.9384, p= 0.2168) 表明, 随机效应模型不能被空间或时间固定效应替代或拒绝。一般而言, 只有当时域范围T足够大时, 空间固定效应才能够被估算^[54], 而由于本研究中时域 (T = 10) 较短, 采用具有随机效应的SDM更合适。此外, 通过H₀:γ = 0和H_0：γ + δ β = 0两种假设进一步验证SDM能否被简化为SLM或SEM。结果表明, SDM可简化为SLM (Wald 验证：18.9158, p< 0.01) 和SEM (Wald test: 20.7649, p< 0.01) 的假设都不成立 (表3), 因此, 具有随机效应的SDM为最优模型。其次, 创新产出和创新投入的SDM参数估计结果表明 (表3), 除了RDE变量外, SDM中所有解释变量的参数估计均很显著, 但是, 由于模型中纳入了空间滞后解释变量与被解释变量, 估计结果不能直接反映其边际效应, 也难以准确衡量创新投入变量对创新产出变量直接影响^[53], 因此, 需要对SDM求偏微分来检验创新产出变量和创新投入变量的直接效应和空间溢出效应 (表4)。

表3 SDM参数估计 Tab. 3 Parameter estimates of SDM

表4 SDM直接效应和间接效应估计 Tab. 4 Direct and indirect effect estimates of SDM

由于区域创新过程中反馈效应的存在, 创新投入变量的直接效应不同于其参数估计值, 这种反馈作用部分源于PAT变量的空间滞后系数, 部分源于其自身的空间滞后系数^[53]。例如, RDE的弹性系数为0.073244, 其直接效应为0.0964, 造成这种明显差异的原因部分源于W* RDE系数的统计显著为正, 部分源于空间滞后因变量 (W* PAT) 也显著为正。类似的, 由于RDP和PCH两个解释变量的空间滞后系数 (W* RDP 和 W* PCH) 均不显著, 其直接效应和参数估计弹性系数差异主要源于空间滞后变量PAT (W* PAT)。其中, RDP的反馈效应为0.007146, 仅为其直接效应的3.6172%; PCH的反馈效应为0.010531, 仅为其直接效应的5.6415%。由此不难看出, 不同的变量间的反馈效应存在较大的差异。此外, 空间滞后PAT变量统计显著性, 表明其溢出效应的地理区域跨越了省区边界。同时, 某一省区及其相邻省区创新活动的空间平均权重呈正相关, 表明相邻省区创新活动的溢出对本省区的创新活动亦具有实质性影响。同时, 比对分析表3和表4, 空间滞后创新投入变量的参数估计和SDM弹性系数间存在较大的差异, 表明在空间回归模型中, 参数估计结果和空间滞后变量均难以准确衡量间接效应的大小和显著性^[47]。例如, 空间滞后RDE变量的参数估计值为0.498953, 而其间接效应估计值为0.6146; 空间滞后GDP变量的参数估计在5%水平统计显著时, 其间接效应并不具有统计上的显著性。此外, RDP和PCH 变量的间接效不具有统计上的显著性, 表明这两个解释变量只有局部效应, 仅影响某一省区自身的创新产出, 而RDE变量的间接效应具有统计上的显著性, 说明其对相邻省区的创新活动具有显著的溢出效应。依据LeSage 和Pace对知识溢出效应的研究, 两种视角可解释间接效应：一种是某一区域对其他区域的影响; 另一种是其它区域对某一特定区域的影响^[48]。以RDE为例, 考虑某一具体省区对其它相邻省区的影响, 该省区研发支出每增加1%, 将会促进相邻省区创新产出提高0.6146%, 从另一个视角看, 某一省区的相邻省区研发支出每增加1%, 将会使该省区创新产出提升0.6146%。

4 结论与讨论

本研究应用探索性空间数据分析和验证性空间数据分析方法, 分析了中国区域创新的时空动态, 阐明了创新产出与创新投入的时空耦合特征及作用机制。研究结论为中国省区创新活动的时空维度的分析提供了新的视角。主要结论如下：

(1) 中国省区创新活动的空间分布极不平衡, 呈现明显的“ 沿海— 内陆” 分化格局。东部沿海省区专利申请数超过全国总量的65%, 年均增长率达24.07%, 在全国区域创新活动中居于压倒性地位。中国区域创新具有明显的空间集聚特征, 创新活动进一步向东部沿海和中部内陆地区集聚, 并形成了以江苏、广东、浙江等为核心的东部沿海创新带和以陕西、湖北、重庆、四川、湖南等为核心的中部内陆创新区。

(2) 探索性空间数据分析结果表明, 创新产出与创新投入的空间集聚随时间推移不断强化, 通过识别其不同时期各类型“ 热点” , 表明中国区域创新产出的“ 热点” 与创新投入变量的“ 热点” 具有高度的时空耦合特征。采用具有随机效应的SDM, 从验证性视角阐明了中国区域创新产出与创新投入的时空关系, 研究表明, RDE、RDP、GDP和PCH等变量对创新产出具有显著的影响, 创新活动的溢出的地理区域跨越了省区边界, 由于空间依赖性的存在, 省区间创新活动具有反馈效应, 相邻省区的知识溢出对该省区的创新活动具有实质性影响。

(3) 通过对中国区域创新时空动态的量化研究, 进一步佐证已有研究中关于区域间存在正的知识溢出效应的重要论断, 并从创新产出和创新投入动态关系的视角, 阐明知识创新具有双向的溢出效应, 国家或区域的创新发展不仅需要提高自身研发和技术水平, 而且需要不断提升吸纳区外知识的能力, 研究结论可为促进中国省区创新产出和政策设计提供科学参考。

本研究选择中国31个省区12年的时空数据, 采用探索性空间数据分析和验证性空间数据分析方法, 较为客观的阐释了中国区域创新的时空动态。但是, 由于样本数据和时域节点相对较少, 研究结果可能并未充分揭示中国区域创新的时空变化规律, 需要在后续研究中深入开展区域创新的多时域、多尺度和多机制分析。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Lin G C S, Wang C. Technological innovation in China's high-tech sector: Insights from a 2008 survey of the integrated circuit design industry in Shanghai. Eurasian Geography and Economics, 2009, 50(4): 402-424. [本文引用:1]
[2]	Romer P M. Endogenous technological change. The Journal of Political Economy, 1990, 98(5): 71-102. [本文引用:1]
[3]	Bottazzi L, Peri G. Innovation and spillovers in regions: Evidence from European patent data. European Economic Review, 2003, 47(4): 687-710. [本文引用:1]
[4]	Pavitt K. The globalizing learning economy. Academy of Management Review, 2002, 27(1): 125-127. [本文引用:1]
[5]	Feldman M P. The Geography of Innovation. Boston: Kluwer Academic Publishers. 1994. [本文引用:1]
[6]	Moreno R, Paci R, Usai S. Spatial spillovers and innovation activity in European regions. Environment and Planning A, 2005, 37(10): 1793-1812. [本文引用:1]
[7]	LeSage J P, Fischer M M, Scherngell T. Knowledge spillovers across Europe: Evidence from a Poisson spatial interaction model with spatial effects. Papers in Regional Science, 2007, 86(3): 393-421. [本文引用:1]
[8]	Fischer M M, Scherngell T, Reismann M. Knowledge spillovers and total factor productivity: Evidence using a spatial panel data model. Geographical Analysis, 2009, 41(2): 204-220. [本文引用:1]
[9]	Asheim B T, Gertler M S. The geography of innovation: regional innovation systems//Fagerberg J et al. The Oxford Hand book of Innovation. New York: Oxford University Press, 2006. [本文引用:1]
[10]	Krugman P. Geography and Trade. Cambridge, MA: The MIT Press, 1991. [本文引用:1]
[11]	Jaffe A, Trajtenberg M, Henderson R. Geographic localization of knowledge spillovers as evidenced by patent citations. Quarterly Journal of Economics, 1993, 108(3): 577-598. [本文引用:1]
[12]	Autant-Bernard C. Spatial econometrics of innovation: Recent contributions and research perspectives. Spatial Economic Analysis, 2012, 7(4): 403-419. [本文引用:2]
[13]	Griliches Z. Issues in assessing the contribution of R&D to productivity growth. Bell Journal of Economics, 1979, 10(1): 92-116. [本文引用:1]
[14]	Jaffe A B. Technological opportunity and spillovers of R&D: Evidence from firm's patents, profits and market value. American Economic Review, 1986, 76(5): 984-1001. [本文引用:1]
[15]	Anselin L, Varga A, Acs Z J. Geographical spillovers and university research: A spatial econometric perspective. Growth and Change, 2000, 31(4): 501-515. [本文引用:2]
[16]	Fischer M M, Slavtchev V. Universities and innovation in space. Industry and Innovation, 2007, 14(2): 201-218. [本文引用:1]
[17]	Gu Baoguo, Qiao Yanqing, Gu Weiyu. Research on the regional difference of spillover effect from technology transfer by MNCs. China Soft Science Magazine, 2005, 20(10): 100-105. [顾保国, 乔延清, 顾炜宇. 跨国公司技术转移溢出效应区域差异分析. 中国软科学, 2005, 20(10): 100-105. ] [本文引用:1]
[18]	Liu Hedong. Empirical research on spillover effects of regional innovation: Analysis based on dynamic panel model of beyond knowledge production function. Studies in Science of Science, 2011, 19(7): 1087-1093. [刘和东. 区域创新溢出效应的实证研究: 基于超越知识生产函数的动态面板模型分析. 科学学研究, 2011, 19(7): 1087-1093. ] [本文引用:1] [CJCR: 1.341]
[19]	Wu Yuming, He Jiankun. Spatial econometric analysis of R&D spillovers and regional innovation cluster. Journal of Management Sciences in China, 2008, 11(4): 59-66. [吴玉鸣, 何建坤. 研发溢出、区域创新集群的空间计量经济分析. 管理科学学报, 2008, 11(4): 59-66. ] [本文引用:1] [CJCR: 1.411]
[20]	Zhang Yuming, Nie Yanhua, Li Kai. An empirical analysis on the impact of knowledge spillovers on regional innovative output: A case of high technology industry. Soft Science, 2009, 23(7): 99-102. [张玉明, 聂艳华, 李凯. 知识溢出对区域创新产出影响的实证分析: 以高技术产业为例. 软科学, 2009, 23(7): 99-102. ] [本文引用:1] [CJCR: 0.8047]
[21]	Liu Manfeng, Tang Houxing. Empirical study on effect of knowledge spillovers based on spatial Durbin model. Science & Technology Progress and Policy, 2010, 27(18): 28-33. [刘满凤, 唐厚兴. 基于空间Durbin模型的区域知识溢出效应实证研究. 科技进步与对策, 2010, 27(18): 28-33. ] [本文引用:1]
[22]	Bai Shaojun, Zhao Liyu. Innovation production and spillover effects in R&D activities based on a spatial panel model. Science & Technology Progress and Policy, 2010, 27(21): 1-4. [白少君, 赵立雨. 基于空间面板数据模型的R&D活动中知识生产与溢出效应研究. 科技进步与对策, 2010, 27(21): 1-4. ] [本文引用:1]
[23]	Martin S. Spillovers, appropriability, and R&D. Journal of Economics, 2002, 75(1): 1-32. [本文引用:1]
[24]	Cheng Yeqing, Deng Jixiang. Spatio-temporal pattern changes and its driving factors of urban-rural integrated development level in the major grain-producing areas of central Jilin Province. Acta Geographica Sinica, 2010, 65(12): 1591-1601. [程叶青, 邓吉祥. 吉林中部粮食主产区城乡综合发展水平格局特征. 地理学报, 2010, 65(12): 1591-1601. ] [本文引用:1] [CJCR: 2.937]
[25]	Cheng Yeqing, Wang Yanfei, Wang Zheye et al. Changing rural development inequality in Jilin Province, Northeast China. Chinese Geographical Science, 2013, 23(5): 620-633. [本文引用:1] [JCR: 0.5] [CJCR: 0.7263]
[26]	Li Guoping, Wang Chunyang. Spatial characteristics and dynamic changes of provincial innovation output in China: An investigation using the ESDA. Geographical Research, 2012, 31(1): 95-106. [李国平, 王春杨. 我国省域创新产出的空间特征和时空演化: 基于探索性空间数据分析的实证. 地理研究, 2012, 31(1): 95-106. ] [本文引用:1]
[27]	Lim U. The spatial distribution of innovative activity in US metropolitan areas: Evidence from patent data. Journal of Regional Analysis and Policy, 2003, 33(2): 97-126. [本文引用:1]
[28]	Jaffe A B. Real effects of academic research. The American Economic Review, 1989, 79(5): 957-970. [本文引用:2]
[29]	Anselin L, Varga A, Acs Z J. Local geographic spillovers between university research and high technology innovations. Journal of urban economics, 1997, 42(3): 422-448. [本文引用:1]
[30]	Bode. The spatial pattern of localized R&D spillovers: An empirical investigation for Germany. Journal of Economic Geography, 2004, 4(1): 43-64. [本文引用:1]
[31]	Griliches Z. Patent statistics as economic indicators: A survey. Journal of Economic Literature, 1990, 28(4): 1661-1707. [本文引用:1]
[32]	Archibugi D. In search of a useful measure of technological innovation (To make economists happy without discontenting technologists). Technological Forecasting and Social Change, 1988, 35(3): 253-277. [本文引用:1]
[33]	Basberg B L. Technological change in the Norwegian whaling industry: A case-study in the use of patent-statistics as a technology indicator. Research Policy, 1982, 11(3): 163-171. [本文引用:1]
[34]	Polanyi M. Knowing and being. Mind, 1961, LXX(280): 458-470. [本文引用:1]
[35]	Cohen W M, Klepper S. The tradeoff between firm size and diversity in the pursuit of technological progress, Small Business Economics, 1992, 4(1): 1-14. [本文引用:1]
[36]	Furman J L, Porter M E, Stern S. The determinants of national innovative capacity. Research Policy, 2002, 31(6): 899-933. [本文引用:1]
[37]	Liu Shunzhong, Guan Jiancheng. The evaluation on the innovating performance of regional innovation systems. Studies in Science of Science, 2002, 20(1): 75-78. [刘顺忠, 官建成. 区域创新系统创新绩效的评价. 科学学研究, 2002, 20(1): 75-78. ] [本文引用:1] [CJCR: 1.341]
[38]	Fang Yuanping, Xie Man. The effect of innovation elements agglomeration on regional innovation output: Based on Chinese provinces and cities' ESDA-GWR Analysis. Economic Geography, 2012, 32(9): 8-14. [方远平, 谢蔓. 创新要素的空间分布及其对区域创新产出的影响: 基于中国省域的ESDA-GWR分析. 经济地理, 2012, 32(9): 8-14. ] [本文引用:1]
[39]	China State Statistics Bureau. China Statistical Yearbook (2000-2012). Beijing: China Statistics Press, 2000-2012. [国家统计局. 中国统计年鉴 (2000-2012). 北京: 中国统计出版社, 2000-2012. ] [本文引用:1]
[40]	Statistics Bureau of China, Ministry of Science and Technology of China. China Statistical Yearbook on Science and Technology, 2000-2012. Beijing: China Statistics Press, 2000-2012. [国家统计局, 中华人民共和国科学与技术部. 中国科技统计年鉴 (2000-2012). 北京: 中国统计出版社, 2000-2012. ] [本文引用:1]
[41]	Anselin L. Exploring spatial data with GeoDa: A workbook. Center for Spatially Integrated Social Science, 2005. [本文引用:2]
[42]	Anselin L. GIS research infrastructure for spatial analysis of real estate markets. Journal of Housing Research, 1998, 9(1): 113-133. [本文引用:1]
[43]	Anselin L. Local indicators of spatial association: LISA. Geographical analysis, 1995, 27(2): 93-115. [本文引用:1]
[44]	Ord J K, Getis A. Testing for local spatial autocorrelation in the presence of global autocorrelation. Journal of Regional Science, 2001, 41(3): 411-432. [本文引用:1]
[45]	Ye X Y, Wu L. Analyzing the dynamics of homicide patterns in Chicago: ESDA and spatial panel approaches. Applied Geography, 2011, 31(2): 800-807. [本文引用:2]
[46]	Anselin L, Le Gallo J, Jayet H. Spatial panel econometrics//Matyas L, Sevestre P. The Econometrics of Panel Data: Fundamentals and Recent Developments in Theory and Practice. Berlin, German: Springer-Verlag, 2008. [本文引用:1]
[47]	LeSage J P, Pace R K. Introduction to Spatial Econometrics. New York: Taylor & Francis-CRC Press. 2009. [本文引用:2]
[48]	Lee L F, Yu J. Some recent developments in spatial panel data models. Regional Science and Urban Economics, 2010, 40(5): 255-271. [本文引用:2]
[49]	LeSage J P, Pace R K. Spatial econometric modeling of origin-destination flows. Journal of Regional Science, 2008, 48(5): 941-967. [本文引用:1]
[50]	Sun Y F. China's national innovation system in transition. Eurasian Geography and Economics. 2002, 43(6): 476-492. [本文引用:1]
[51]	Rey S, Ye X Y. Comparative spatial dynamics of regional systems//Páez J et al. Progress in Spatial Analysis: Theory, Computation, and Thematic Applications. Berlin: Springer, 2010. [本文引用:1]
[52]	Ye X Y, Rey S. A framework for exploratory space-time analysis of economic data. The Annals of Regional Science, 2013, 50(1): 315-339. [本文引用:1]
[53]	Elhorst J P. http://www.progressingeography.com/richhtml/0375-5444/html_resources/www.regroningen.nl/elhorst/doc/Matlab-paper.pdf,2010. [本文引用:3]
[54]	Elhorst J P. Spatial panel data models//Fischer M M, Getis A. Hand book of Applied Spatial Analysis. Berlin: Springer, 2010: 377-407. [本文引用:1]

2009

0.0

... 1 引言在经济全球化背景下,世界各国都关注到创新对经济发展的至关重要作用^[1] ...

1990

0.0

... 新经济增长理论认为知识型创新是促进经济增长和提高生活标准的主要驱动力^[2],研发过程中通过资源投入产生新的知识,其扩散过程是现代市场经济增长机制的核心^[3] ...

2003

0.0

Bottazzi

, Peri

Innovation and spillovers in regions: Evidence from European patent data.

European Economic Review, 2003, 47(4): 687-710.

2002

0.0

... 创新是一种以新的方式生产新知识或融合已有知识的过程,知识为创新性价值创造 (譬如创新过程) 奠定了最为重要的基础^[4] ...

1994

0.0

... 然而,知识创新来源于一定的支撑 (如企业、研究机构和高等教育机构等),而这些支撑又趋向于集中在某些具体区位,这就决定了发明和创造不会均衡分布于空间,而是趋向于在一定区位聚集^[5,6] ...

2005

0.0

2007

0.0

LeSage J

, Fischer M

, Scherngell

. Knowledge spillovers across Europe: Evidence from a Poisson spatial interaction model with spatial effects. Papers in Regional Science, 2007, 86(3): 393-421.

1 McCoy College of Business Administration, Department of Finance and Economics, Texas State University, San Marcos, Texas 78666, USA (e-mail: jlesage@spatial-econometrics.com ) 2 Institute for Economic Geography and GIScience, Vienna University of Economics and Business Administration, A-1090 Vienna, Austria (e-mail: manfred.fischer@wu-wien.ac.at ; thomas.scherngell@wu-wien.ac.at )

> Abstract. We apply a Bayesian hierarchical Poisson spatial interaction model to the paper trail left by patent citations between high-technology patents in Europe to identify and measure spatial separation effects of interregional knowledge flows. The model introduced here is novel in that it allows for spatially structured origin and destination effects for the regions. Estimation of the model is carried out within a Bayesian framework using data augmentation and Markov Chain Monte Carlo (MCMC) methods, related to recent work in Frühwirth-Schnatter and Wagner (2004 ). This allows MCMC sampling from well-known distribution families, and thus provides a substantial improvement over MCMC estimation based on Metropolis-Hastings sampling from non-standard conditional distributions.

... 实证研究证明,知识流动遵循地理衰减规律,意味着地理距离的增加会提高知识传播成本^[7,8] ...

2009

0.0

Fischer M

, Scherngell

, Reismann

Knowledge spillovers and total factor productivity: Evidence using a spatial panel data model.

Geographical Analysis, 2009, 41(2): 204-220.

Institute for Economic Geography and GIScience, Vienna University of Economics and Business, Vienna, Austria * Manfred M. Fischer, Chair for Economic Geography, Institute for Economic Geography & GIScience, Vienna University of Economics and Business, Nordbergstr. 15/4/A, A-1090 Vienna, Austria e-mail: manfred.fischer@wu-wien.ac.at

> This article investigates the impact of knowledge capital stocks on total factor productivity (TFP) through the lens of the knowledge capital model proposed by Griliches (1979) , augmented with a spatially discounted cross-region knowledge spillover pool variable. The objective is to shift attention from firms and industries to regions and to estimate the impact of cross-region knowledge spillovers on TFP in Europe. The dependent variable is the region-level TFP, measured in terms of the superlative TFP index suggested by Caves, Christensen, and Diewert (1982) . This index describes how efficiently each region transforms physical capital and labor into output. The explanatory variables are internal and out-of-region stocks of knowledge, the latter capturing the contribution of cross-region knowledge spillovers. We construct patent stocks to proxy annual regional knowledge capital stocks for N =203 regions during 1997–2002. In estimating the effects, we implement a spatial panel data model that controls for spatial autocorrelation as well as individual heterogeneity across regions. The findings provide a fairly remarkable confirmation of the role of knowledge capital contributing to productivity differences among regions and add an important spatial dimension to discussions in the literature by showing that productivity effects of knowledge spillovers increase with geographic proximity.

... 实证研究证明,知识流动遵循地理衰减规律,意味着地理距离的增加会提高知识传播成本^[7,8] ...

2006

0.0

... 此外,某一区域创新人员生产的新知识将随着时间的推移不仅会扩散到同一区域的其它创新人员 (区内知识溢出),而且会扩散到其他区域的创新人员 (区际知识溢出) ^[9] ...

1991

0.0

... Krugman 认为知识流动是看不见的,知识溢出的实证测度是不可能的^[10] ...

1993

0.0

... 但是,Jaffe等认为专利记录可能很好的留下知识溢出的纸质痕迹,因此,专利引证可以被视为知识溢出的一个指标^[11] ...

2012

0.0

... 知识溢出的强度可以通过引入空间距离作为解释变量的专利引证强度进行评估,这种空间相互作用模型已被大量的实证研究所采用^[12] ...

... 正如Autant-Bernard指出,创新过程具有明确的空间异质性和空间依赖性,在知识生产函数中,通过空间计量工具中的空间自相关可正确计算出模型系数,且能区分其直接和间接影响^[12] ...

1979

0.0

... 研发投入,也取决于通过地理邻居获取的研发投入^[13,14] ...

1986

0.0

... 研发投入,也取决于通过地理邻居获取的研发投入^[13,14] ...

2000

0.0

Anselin

, Varga

, Acs Z

Geographical spillovers and university research: A spatial econometric perspective.

Growth and Change, 2000, 31(4): 501-515.

1 Regional Economics Applications Laboratory (REAL) and Agricultural and Consumer Economics, University of Illinois at Urbana–Champaign, 2 Institute for Economic Geography, Regional Development and Environmental Management, Vienna University of Economics and Business Austria, 3 U.S. Bureau of the Census and Merrick School of Business, University of Baltimore

> Using data for U.S. metropolitan statistical areas, an earlier study of aggregate local geographic research spillovers generated by universities (Anselin et al.1997) was extended to a sectorally disaggregated level. These findings suggest the existence of significant sectoral variation with respect to local university effects on innovation. Apparent differences were found across sectors with respect to the “mix” of applied local knowledge inputs in general, and the extent to which university research plays a role in innovation in particular. The main conclusion is that local university spillovers seem to be specific to certain industries, such that at the two-digit SIC level, no university spillover effects are at work in the Drugs and Chemicals (SIC28) and in the Machinery (SIC35) sectors. On the contrary, very strong and significant university research spillovers are evidenced in the Electronics (SIC36) and the Instruments (SIC38) industries. These spillovers extend beyond the boundary of the MSA within a 75-mile range from the central city.

... 随着空间计量经济学快速发展,空间计量模型逐渐被应用于分析区域创新和知识溢出效应^[15] ...

... 因此,本研究仍将专利申请数作为衡量创新产出的表征指标,并基于最先被Griliches 验证并经过不断发展的知识生产函数^[15],采用Jaffe的分析框架^[28],选择4个创新投入变量作为衡量区域创新的决定性因素 ...

2007

0.0

... 然而,除了Lesage等通过解释知识溢出来源地和目的地区域的异质性纠正空间自相关模型外,现有研究极少将空间计量工具引入到空间相互作用模型的分析框架^[16] ...

2005

0.0

... 中国针对知识溢出的文献日益增多,空间计量工具在知识生产函数中的应用研究快速增长^[17,18],空间误差模型和空间杜宾模型等被应用于阐释高校学术研究溢出效应和高新技术产业创新等领域^[19,20],研究表明,知识溢出随地理距离而变化^[21],研发人员对区域创新有积极的溢出效应^[22] ...

2011

0.0

1.341

2008

0.0

1.411

2009

0.0

0.8047

Zhang

Yuming

, Nie

Yanhua

, Li

Kai.

An empirical analysis on the impact of knowledge spillovers on regional innovative output: A case of high technology industry.

Soft Science, 2009, 23(7): 99-102.

[张玉明, 聂艳华, 李凯. 知识溢出对区域创新产出影响的实证分析: 以高技术产业为例. 软科学, 2009, 23(7): 99-102. ]

运用空间计量经济学模型,以高技术产业为例,对三种类型的知识溢出对中国省际区域创新产出的影响以及空间相关性问题进行了实证分析.结果发现,中国31个省际区域的创新活动存在空间依赖性,高技术产业的专业化、多样化,省际区域的人力资本对区域创新产出具有正向促进作用.区域创新活动的空间依赖性要求各省际区域在制定区域经济政策时要充分考虑知识溢出的地理特性,加强区域合作. Abstract： Using a spatial econometric model,this paper analyzes the effects of three kinds of knowledge spillovers on innovative output and spatial dependence based on a case of high technology industry. It is found that the inno-vative activity of China' s 31 provincial regions have spatial dependence, and the specialization and diversity of the high technology industry, and provincial regional human capital has the contribution to the innovative output. The spatial dependence of the regional innovative activity desire that when the regional economic policy has been made for every province, the geography trait of knowledge spillovers should be considered, so as to strengthen the region-al cooperation.

2010

0.0

2010

0.0

2002

0.0

Martin

Spillovers, appropriability, and R&D.

Journal of Economics, 2002, 75(1): 1-32.

1.FEE/F&O, University of Amsterdam, Roetersstraat 11, 1018 WB Amsterdam, The Netherlands (e-mail: smart@fee.uva.nl.) NL

... 但是,已有研究主要从创新投入视角分析了区域知识溢出效应,未能突出创新产出溢出效应在创新活动中的重要作用^[23] ...

2010

0.0

2.937

Cheng

Yeqing

, Deng

Jixiang.

Spatio-temporal pattern changes and its driving factors of urban-rural integrated development level in the major grain-producing areas of central Jilin Province.

Acta Geographica Sinica, 2010, 65(12): 1591-1601.

[程叶青, 邓吉祥. 吉林中部粮食主产区城乡综合发展水平格局特征. 地理学报, 2010, 65(12): 1591-1601. ]

By the methods of Principal Component Analysis, Multi-objective Weighted Model, Markov Chains and ESDA, and based on the data of 2000, 2003 and 2007 of 24 spatial units in the major grain-producing areas of central Jilin Province, the spatio-temporal pattern change and its driving factors of urban-rural integrated development level were discussed. The results are shown as follows. First, there exists a phenomenon of “Club Convergence” in regional urban-rural development, and the spatial discrepancy of urban-rural integrated development level in the study area has become greater; Second, there was an obvious trend in the “Polarization”of urban-rural integrated development level, i.e., the higher level spatial units were concentrated in the five prefecture-level municipal districts, and the lower level spatial units were mainly in the central region along the Harbin-Dalian Railway, thus formed a “Dumbbell”-shaped continuous distribution area. It may fall into the“Matthew Effect”that the strong will become stronger and the weak will be constantly weaker. Finally, according to the Principal Component Analysis, it can be concluded that the economic strength, spatial location and income level of residents were the main driving factors of spatio-temporal pattern change of the urban-rural integrated development level in the major grain-producing area of central Jilin Province.

1. Northeast Institute of Geography and Agroecology, CAS, Changchun 130012, China; 2. Department of Urban and Environmental Science, Northwest University, Xi'an 710127, China

运用主成分分析、多目标加权求和模型、马尔可夫链和ESDA方法，在GIS 技术支持下，基于吉林省中部粮食主产区24 个空间单元2000 年、2003 年、2007 年3 个时间断面的数据，探讨该区城乡综合发展水平时空格局演变特征及其动力因子。研究结果表明：① 区域城乡发展存在“俱乐部趋同”现象，城乡综合发展水平的空间差异趋于扩大；② 区域城乡综合发展水平“两极分化”明显，高水平空间单元集中在5 个地级市辖区，低水平空间单元进一步向哈大铁路沿线集聚，并在其北侧形成“哑铃”状连续分布区，该区域有可能陷于强者愈强，弱者恒弱的“马太效应”；③ 主成分分析结果表明，城乡经济实力、空间区位、居民收入等是吉林省中部粮食主产区城乡综合发展水平时空格局演变的主要动力因子。

... GIS技术及探索性数据分析方法 (Exploratory Spatial Data Analysis,简称ESDA) 为区域发展的空间分析提供了强有力的工具,且ESDA在近年来区域发展不平衡的实证研究中得到广泛应用^[24,25],一些最新的研究也应用该方法探讨了知识创新的空间分布等问题^[26,27] ...

2013

0.5

0.7263

Cheng

Yeqing

, Wang

Yanfei

, Wang

Zheye

et al. Changing rural development inequality in Jilin Province, Northeast China. Chinese Geographical Science, 2013, 23(5): 620-633.

1. Northeast Institute of Geography and Agroecology, Chinese Academy of Sciences, Changchun, 130102, China 2. University of Chinese Academy of Sciences, Beijing, 100049, China 3. Department of Urban Planning and Design, Nanjing University, Nanjing, 210093, China

Rural development inequality is an important practical issue during the course of full establishment of a ‘moderately well-off society’ in modern China, and the objective understanding and evaluation of the status and regional inequality of rural development can provide scientific basis for ‘building a new countryside’ and coordination development of rural-urban regions. Based on the county-level data of 2000, 2005 and 2009, this paper examines the rural development inequality of Jilin Province in Northeast China by establishing a rural development index. The spatio-temporal dynamic patterns and domain factors are discussed by using the method of exploratory spatial data analysis and multi-regression model. The results are shown as follows. Firstly, most of the counties were in lower development level, which accounted for 58.3%, 62.5% and 66.7% of the total counties in 2000, 2005 and 2009, respectively. The characteristics of spatial inequality were very obvious at county level. For example, rural development level of Changchun Proper and the proper of seven prefecture-level cities were much higher than that of the surrounding regions. The counties in the eastern and northern Jilin Province were the lowest regions of rural development level, while the middle counties were the rapid growth areas in rural economy. Secondly, Moran’s I of rural development index (RDI) was 0.01, −0.16 and −0.06 in 2000, 2005 and 2009, respectively, which indicated that spatial agglomeration of RDI was not obvious in Jilin Province, and took on the characteristic of random distribution. The counties of both the units and its adjacent units have higher development level (HH) were transferred from the western areas to the eastern areas, while the countries of both the units and its adjacent units have lower development level (LL) were diffused from the eastern to middle and western Jilin Province. Finally, the result of multi-regression analysis showed that the improvement of agricultural production condition, development of agricultural economics and the adjustment of industrial structure were the domain factors affecting rural development inequality of Jilin Province in the later ten years.

2012

0.0

Guoping

, Wang

Chunyang.

Spatial characteristics and dynamic changes of provincial innovation output in China: An investigation using the ESDA.

Geographical Research, 2012, 31(1): 95-106.

[李国平, 王春杨. 我国省域创新产出的空间特征和时空演化: 基于探索性空间数据分析的实证. 地理研究, 2012, 31(1): 95-106. ]

Innovation activities in each region not only depend on their own characteristics,but also on those of the regions that form the neighborhood to which it belongs.Regional spillover as a spatial interaction is important in explaining agglomeration,innovation and regional growth.A great deal of literature has deeply dealt with the issue from a spatial perspective since the 1990s,especially in the context of urban and regional studies.Unfortunately,the traditional approaches to regional innovation suppose that each region is independent from others.This paper uses spatial statistical techniques to establish the statistical relations among data according to the geographical locations.It aims to understand the spatial dependence and autocorrelation related to geographical locations.Using the methods of exploratory spatial data analysis(ESDA) and spatial analysis software,this paper analyzes the spatial distribution of innovation outputs,measured by the number of patient applications,throughout 31 Chinese provinces from 1997 to 2008.The visual patent distribution plot has shown the distribution of innovation outputs at the provincial level and its spatial dynamic changes.A significantly high level of spatial concentration of innovation outputs among Chinese provinces has been captured by the computed spatial Gini coefficient and the Concentration Ratio,and the concentration level has increased steadily over the past 10 years.The analysis using the Moran’s I statistics gives the strong evidence of spatial autocorrelation in innovation activities among provinces,while the concentration pattern of innovation activities among provinces and its changes over time have been revealed by using the local Moran’s I and the Moran scatter plot,which indicate the clustering nature of the spatial distribution of provincial innovation activities.Spatial Gini coefficient and Moran’s I index have indicated that innovation activities of Chinese provinces are not randomly distributed.Our findings suggest that innovation activities are spatially differentiated among Chinese provinces over the 10 years,and innovation activities at the provincial level are highly localized.This study can provide a scientific basis for the intuitive expression of the spatial correlation of innovation outputs among provinces,and puts forward that the spatial statistical analysis could present some references valuable for analyzing spatial structure and patterns and policy-making.

School of Government, Peking University, Beijing 100871, China

以我国31个省域作为空间观测单元,以专利申请受理数作为创新产出的衡量指标,对我国1997～2008年期间省域创新产出的空间分布进行了探索性空间数据分析(ESDA)。通过计算区位基尼系数和集中度指数,发现我国的创新活动显示了相当高水平的空间集中,并且这种集中程度在过去的十多年里表现出了稳定的增长趋势;对全局的Moran’s I 统计分析表明:省际创新活动之间存在着显著的空间自相关(空间依赖性),证明了知识溢出的存在性和空间局限性;对局部的Moran’s I 分析进一步揭示了省际创新活动水平的相关模式,Moran散点图刻画了创新活动的空间集聚模式及其时空演变态势。研究结果说明经过十几年的发展,我国省域创新活动的地域性特征十分显著。

2003

0.0

1989

0.0

... 已有文献大多以专利作为创新产出的定量指标^[28,29,30],尽管学术界在探讨哪些指标最适合测度创新产出的问题上未形成共识,所选择的指标也仅能部分地反映区域创新程度^[31] ...

1997

0.0

Anselin

, Varga

, Acs Z

Local geographic spillovers between university research and high technology innovations.

Journal of urban economics, 1997, 42(3): 422-448.

2004

0.0

1990

0.0

1988

0.0

... 但是,专利在创新过程中的每个阶段都扮演重要角色,专利数据为分析区域知识创新的时空分布提供了重要的信息^[32,33],仍然是到目前为止刻画知识创新最为合适与常用的指标 ...

1982

0.0

Basberg B

Technological change in the Norwegian whaling industry: A case-study in the use of patent-statistics as a technology indicator.

Research Policy, 1982, 11(3): 163-171.

1961

0.0

... 因为无论专利最终被批准与否,申请这个产权都包含了支持者重要的成本,并注重发明相关的新颖性和盈利能力特征^[34] ...

1992

0.0

... Cohen and Klepper指出研发工作是知识创新最重要源泉^[35] ...

2002

0.0

Furman J

, Porter M

, Stern

The determinants of national innovative capacity.

Research Policy, 2002, 31(6): 899-933.

... 除了研发工作,内生经济理论强调另一个生产决定性因素的经济理念：技术绩效的经济综合水平^[36] ...

2002

0.0

1.341

Liu

Shunzhong

, Guan

Jiancheng.

The evaluation on the innovating performance of regional innovation systems.

Studies in Science of Science, 2002, 20(1): 75-78.

[刘顺忠, 官建成. 区域创新系统创新绩效的评价. 科学学研究, 2002, 20(1): 75-78. ]

Based on the method of DEA,this paper analyses the performance of the regional innovation systems of our country. According to the characteristics of the concerned innovation system,the regional innovation systems are classified. We give the different suggestions about how to improve the innovating performance for the different categories of regional innovation systems.

Research Center for Technology Management & Technological Innovation, Beijing University of Aeronautics and Astronautics, Beijing 100083, China

客观评价区域创新系统的创新绩效是制定区域创新政策的前提。本文运用DEA方法分析我国各地区创新系统的特点,并对各系统的创新绩效进行了评价。根据各创新系统的特点和创新绩效,将我国各地区的区域创新系统进行分类。针对每一类创新系统,提出了制定区域创新政策的建议。

... 借鉴已有研究成果^[37,38],采用滞后一年的创新投入变量,由于输入变量与可度量的产出变量间的转化需要一些时间,采用一年时间的滞后可提升观测值的数量和自由度 ...

2012

0.0

2012

0.0

... 原始数据均来源于《中国统计年鉴》(2000-2012) 和《中国科技统计年鉴》(2000-2012)^[39,40],为保持数据的可比性,各省级单元所有GDP数据均转换为1999年不变价 ...

2000-2012

0.0

2005

0.0

... 2 ESDA：空间自相关分析ESDA是一种在评估和测试之前描述性动态因素来解释空间格局的较为复杂的回归模型^[41],其独特之处在于通过空间权重矩阵建立本区域与周边邻域之间的空间关系,并通过空间滞后向量确定每一个区域的空间邻域状态^[41,42] ...

1998

0.0

1995

0.0

... Moran's I是基于999种排列的排列方法统计推论而得^[43] ...

2001

0.0

Ord J

, Getis

Testing for local spatial autocorrelation in the presence of global autocorrelation.

Journal of Regional Science, 2001, 41(3): 411-432.

1 Georgetowm University, Washington, D.C., 2 San Diego State University, San Diego

> A fundamental concern of spatial analysts is to find patterns in spatial data that lead to the identification of spatial autocorrelation or association. Further, they seek to identify peculiarities in the data set that signify that something out of the ordinary has occurred in one or more regions. In this paper we provide a statistic that tests for local spatial autocorrelation in the presence of the global autocorrelation that is characteristic of heterogeneous spatial data. After identifying the structure of global autocorrelation, we introduce a new measure that may be used to test for local structure. This new statistic Oi is asymptotically normally distributed and allows for straightforward tests of hypotheses. We provide several numerical examples that illustrate the performance of this statistic and compare it with another measure that does not account for global structure.

... ^[44] ...

2011

0.0

Ye X

, Wu

Analyzing the dynamics of homicide patterns in Chicago: ESDA and spatial panel approaches.

Applied Geography, 2011, 31(2): 800-807.

Abstract This paper studies the relationship between homicide rate and socioeconomic factors at community area level in Chicago from 1960 to 1995. Most of prior studies of social disorganization theory are based on cross-sectional spatial regression or longitudinal studies. This research integrates space and time in testing social disorganization theory. First, exploratory spatial data analysis (ESDA) is used to examine dynamic spatial patterns of these indicators. This investigation justifies the estimation of homicide rates across community areas through panel-data models that extend to include spatial lag and spatial error autocorrelation. Research highlights ? This research conducts an empirical study of both the spatial and temporal aspects of homicide patterns at the community area level. ? Spatial panel regression is considered a solution to examine the space–time relationship between crime and neighborhood characteristics. ? Historically formed neighborhoods are desirable units of analysis in social disorganization research.

... 图式,将Anselin的LISA 意义地图拓展到时序关联^[45] ...

... 图式方法解决这个问题^[45] ...

2008

0.0

... 正如Anselin等指出,在阐明观测值的空间依赖 (空间自相关) 时,空间面板数据模型可能包含一个空间滞后因变量或一个空间自回归过程的误差项^[46] ...

2009

0.0

... 前一个为空间滞后模型 (Spatial Lag Model,简称SLM),后一个即为空间误差模型 (Spatial Error Model,简称SEM)^[47] ...

... 同时,比对分析表3和表4,空间滞后创新投入变量的参数估计和SDM弹性系数间存在较大的差异,表明在空间回归模型中,参数估计结果和空间滞后变量均难以准确衡量间接效应的大小和显著性^[47] ...

2010

0.0

Lee L

, Yu

Some recent developments in spatial panel data models.

Regional Science and Urban Economics, 2010, 40(5): 255-271.

Abstract Spatial econometrics has been an ongoing research field. Recently, it has been extended to panel data settings. Spatial panel data models can allow cross sectional dependence as well as state dependence, and can also enable researchers to control for unknown heterogeneity. This paper reports some recent developments in econometric specification and estimation of spatial panel data models. We develop a general framework and specialize it to investigate different spatial and time dynamics. Monte Carlo studies are provided to investigate finite sample properties of estimates and possible consequences of misspecifications. Two applications illustrate the relevance of spatial panel data models for empirical studies.

... 空间杜宾模型 (Spatial Durbin Model,简称SDM) 被认为是第三种空间面板数据模型,采用这种模型的动机源于当处理区域数据样本时可能会增加遗漏变量等问题,表明SDM的一个本质特征是因变量中嵌套了空间依赖,自变量和误差项的参数估计不会受到遗漏变量空间依赖程度的影响^[48] ...

... 另一种是其它区域对某一特定区域的影响^[48] ...

2008

0.0

LeSage J

, Pace R

. Spatial econometric modeling of origin-destination flows. Journal of Regional Science, 2008, 48(5): 941-967.

1 McCoy Endowed Chair of Urban and Regional Economics, Texas State University, San Marcos, Department of Finance and Economics, San Marcos, TX 78666. E-mail: jlesage@spatial-econometrics.com 2 LREC Endowed Chair of Real Estate, Department of Finance, E.J. Ourso College of Business Administration, Louisiana State University, Baton Rouge, LA 70803-6308. E-mail: kelley@pace.am

> ABSTRACT Standard spatial autoregressive models rely on spatial weight structures constructed to model dependence among n regions. Ways of parsimoniously modeling the connectivity among the sample of N = n 2 origin-destination (OD) pairs that arise in a closed system of interregional flows has remained a stumbling block. We overcome this problem by proposing spatial weight structures that model dependence among the N OD pairs in a fashion consistent with standard spatial autoregressive models. This results in a family of spatial OD models introduced here that represent an extension of the spatial regression models described in Anselin (1988) .

... 本研究采用SDM的另一个原因在于测度区内及区际尺度知识溢出效应的可行性,即知识创新的直接效应和间接效应^[49] ...

2002

0.0

... 中国政府已经认识到创新对国家未来经济发展的重要性,并且在引导国家创新系统发展中起到了核心和持久的作用^[50] ...

2010

0.0

... 但是,全局空间自相关分析可能掩盖局部空间信息,会产生一系列问题,时间关联分析中需要纳入局部空间信息^[51,52] ...

2013

0.0

Ye X

, Rey

A framework for exploratory space-time analysis of economic data.

The Annals of Regional Science, 2013, 50(1): 315-339.

1. Center for Regional Development & School of Earth, Environment, and Society, Bowling Green State University, 109 South Hall, Bowling Green, OH, 43403-0181, USA 2. School of Geographical Sciences and Urban Planning, Arizona State University, Tempe, AZ, 85287-5302, USA

The development of exploratory spatial data analysis methods is an active research domain in the field of geographic information science (GIS). At the same time, the coupled space-time attributes of economic phenomena are difficult to be represented and examined. Both GIS and economic geography are faced with the challenges of dealing with the temporal dynamics of geographic processes and spatial dynamics of economic development across scales and dimensions. This paper thus suggests a novel way to generalize the characteristics and the structure of space-time data sets, using regional economic data as the example. Accordingly, a reasonable number of general questions (data analysis tasks) can be abstracted. Then, tools (methods) may be suggested on that basis. The cross-fertilization between exploratory spatial data analysis (ESDA) and spatial economics is also identified and illustrated by the capabilities of these components, which have uncovered some interesting patterns and trends in the spatial income data of China and the United States. Through exploratory analysis of economic data, the detection of rich details of underlying geographical and temporal processes would be the first step toward such cross-fertilization. In addition, this exploratory analytical framework can be applied to other data sets that are also measured for areal units at multiple points in time.

... 但是,全局空间自相关分析可能掩盖局部空间信息,会产生一系列问题,时间关联分析中需要纳入局部空间信息^[51,52] ...

0.0

... 2 验证性空间数据分析采用SDM对创新产出和创新投入进行测试和估算^[53] ...

... 其次,创新产出和创新投入的SDM参数估计结果表明 (表3),除了RDE变量外,SDM中所有解释变量的参数估计均很显著,但是,由于模型中纳入了空间滞后解释变量与被解释变量,估计结果不能直接反映其边际效应,也难以准确衡量创新投入变量对创新产出变量直接影响^[53],因此,需要对SDM求偏微分来检验创新产出变量和创新投入变量的直接效应和空间溢出效应 (表4) ...

... 由于区域创新过程中反馈效应的存在,创新投入变量的直接效应不同于其参数估计值,这种反馈作用部分源于PAT变量的空间滞后系数,部分源于其自身的空间滞后系数^[53] ...

2010

0.0

... 一般而言,只有当时域范围T足够大时,空间固定效应才能够被估算^[54],而由于本研究中时域 (T = 10) 较短,采用具有随机效应的SDM更合适 ...